Эта глава книги посвящена уникальным возможностям системы Maple 9.5/10 в визуализации самых разнообразных вычислений. Рассмотрены возможности и опции двумерной и трехмерной графики, в том числе использующей функциональную окраску. Особое внимание уделено визуализации математических и физических понятий и реализации различных возможностей машинной графики.

Средства для построения графиков в большинстве языков программирования принято считать графическими процедурами или операторами. Однако в СКМ Maple 9.5/10 мы сохраним за ними наименование функций, в силу двух принципиально важных свойств:

• графические средства Maple возвращают некоторые графические объекты, которые размешаются в окне документа — в строке вывода или в отдельном графическом объекте;

• эти объекты можно использовать в качестве значений переменных, то есть переменным можно присваивать значения графических объектов и выполнять над ними соответствующие операции (например, с помощью функции snow выводить на экран несколько графиков).

Графические функции заданы таким образом, что обеспечивают построение типовых графиков без какой-либо особой подготовки. Для этого нужно лишь указать функцию, график которой строится, и пределы изменения независимых переменных. Однако с помощью дополнительных необязательных параметров (опций) можно существенно изменить вид графиков — например, настроить стиль и цвет линий, вывести титульную надпись, изменить вид координатных осей и т.д.

В Maple введены функции быстрого построения графиков. Так, функция smartplot(f) предназначена для создания двумерных графиков. Параметр f может задаваться в виде одиночного выражения или набора выражений, разделяемых запятыми. Задание управляющих параметров в этих графических функциях не предусмотрено; таким образом, их можно считать первичными или черновыми. Для функции построения двумерного графика по умолчанию задан диапазон изменения аргумента -8..8.

Для построения двумерных графиков служит функция plot. Она задается в виде

plot(f, h, v)

plot(f, h, v, o)

где f — визуализируемая функция (или функции), h — переменная с указанием области ее изменения, v — необязательная переменная с указанием области изменения, о — параметр или набор параметров, задающих стиль построения графика (толщину и цвет кривых, тип кривых, метки на них и т.д.).

Самыми простыми формами задания этой функции являются следующие:

• plot(f,xmin..xmax) — построение графика функции f, заданной только своим именем в интервале изменения х от xmin до xmax;

• plot(f(x),x=xmin..xmax) — построение графика функции f(x) в интервале изменения х от xmin до xmax.

Выше приводилось множество примеров применения этой функции. Для нее возможны следующие дополнительные параметры:

• adaptive — включение адаптивного алгоритма построения графиков (детали см. ниже);

• axes — вывод различных типов координат (axes=NORMAL — обычные оси, выводятся по умолчанию, axes=BOXES — график заключается в рамку с осями-шкалами, axes=FRAME — оси в виде перекрещенных линий, axes=NONE — оси не выводятся);

• axesfont — задание шрифтов для подписи делений на координатных осях (см. также параметр font);

• color — задает цвет кривых (см. далее);

• coords — задание типа координатной системы (см. далее);

• discont — задает построение непрерывного графика (значения true или false);

• filled — при filled=true задает окраску цветом, заданным параметром color, для области, ограниченной построенной линией и горизонтальной координатной осью х;

• font — задание шрифта в виде [семейство, стиль, размер];

• labels — задание надписей по координатным осям в виде [X,Y], где Х и Y -надписи по осям х и у графика;

• labeldirections — задает направление надписей по осям [X,Y], где X и Y может иметь строковые значения HORISONTAL (горизонтально) и VERTICAL (вертикально);

• labelfont — задает тип шрифта метод (см. font);

• legend — задает вывод легенды (обозначения кривых);

• linestyle — задание стиля линий (1 — сплошная, 2 — точками, 3 — пунктиром и 4 — штрих-пунктиром);

• numpoints — задает минимальное количество точек на графике (по умолчанию numpoints=49);

• resolutions — задает горизонтальное разрешение устройства вывода (по умолчанию resolutions=200, параметр используется при отключенном адаптивном методе построения графиков);

• sample — задает список параметров для предварительного представления кривых;

• scaling — задает масштаб графика: CONSTRAINED (сжатый) или UNCONSTRAINED (несжатый — по умолчанию);

• size — задает размер шрифта в пунктах;

• style — задает стиль построения графика (POINT — точечный, LINE — линиями);

• symbol — задает вид символа для точек графика (возможны значения BOX — прямоугольник, CROSS — крест, CIRCLE -- окружность, POINT — точка, DIAMOND — ромб);

• symbolsize — установка размеров символов для точек графика (в пунктах, по умолчанию 10);

• title — задает построение заголовка графика (title="string", где string — строка),

• titlefont — определяет шрифт для заголовка (см. font);

• thickness — определяет толщину линий графиков (0, 1, 2, 3, значение по умолчанию — 0);

• view=[A, В] — определяет максимальные и минимальные координаты, в пределах которых график будет отображаться на экране, А=[xmin..xmax], B=[ymin..ymax] (по умолчанию отображается вся кривая);

• xtickmarks — задает минимальное число отметок по оси х;

• ytickmarks — задает минимальное число отметок по оси у.

Параметр adaptive задает работу специального адаптивного алгоритма для построения графиков наилучшего вида. При этом Maple автоматически учитывает кривизну изменения графика и увеличивает число отрезков прямых в тех частях графиков, где их ход заметно отличается от интерполирующей прямой. При задании adaptive=false адаптивный алгоритм построения графиков отключается, а при adaptive=true включается (значение по умолчанию).

С помощью параметра у = ymin..ymax можно задать масштаб графика по вертикали.

Это иллюстрирует рис. 8.1, который заодно показывает применение дополнительных параметров функции plot при построении двумерных графиков.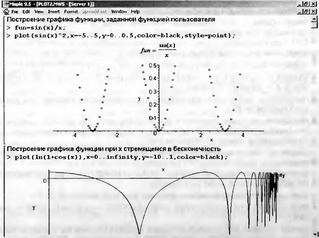

Рис. 8.1. Построение графиков функции с явным указанием масштаба

Изредка встречаются графики функций f(x), которые надо построить при изменении значения x от нуля до бесконечности или даже от минус бесконечности до плюс бесконечности. Бесконечность в таких случаях задается как особая константа infinity. В этом случае переменной x, устремляющейся в бесконечность, откладывается значение arctan(x). Рисунок 8.1 (второй пример) иллюстрирует сказанное.

В версии Maple 9.5 параметр coords задает 15 типов координатных систем для двумерных графиков. По умолчанию используется прямоугольная (декартова) система координат (coords=cartesian). При использовании других координатных систем координаты точек для них (u, v) преобразуются в координаты (х, y) как (u,v)→(x,y). Формулы преобразования координат можно найти в справке.

Maple 9 5 позволяет воспроизводить на одном графике множество кривых с разным стилем, который задается параметром style:

• POINT или point — график выводится по точкам;

• LINE или line — график выводится линией.

Если задано построение графика точками, то параметр symbol позволяет представить точки в виде различных символов, например прямоугольников, крестов, окружностей или ромбов. Другой параметр — color — позволяет использовать обширный набор цветов линий графиков:

aquamarine black  blue    navy   coral

cyan       brown  gold    green  gray

grey       khaki  magenta maroon orange

pink       plum   red     sienna tan

turquoise  violet wheat   white  yellow

Различные цветовые оттенки получаются использованием RGB-комбинаций базовых цветов: red — красный, gray — зеленый, blue — синий. Приведем перевод ряда других составных цветов: black — черный, white — белый, khaki — цвет «хаки», gold — золотистый, orange — оранжевый, violet — фиолетовый, yellow — желтый и т.д. Естественно, что черно-белой печати рисунков вместо цветов получаются градации серого цвета.

Некоторые функции, например tan(x), имеют при определенных значениях х разрывы, причем случается, что значения функции в этом месте устремляются в бесконечность. Функция tan(x), к примеру, в точках разрывов устремляется к +∞ и -∞. Построение графиков таких функций нередко дает плохо предсказуемые результаты. Графический процессор Maple не всегда в состоянии определить оптимальный диапазон по оси ординат, а график функции выглядит весьма непредставительно, если не сказать безобразно (рис. 8.2, первый пример)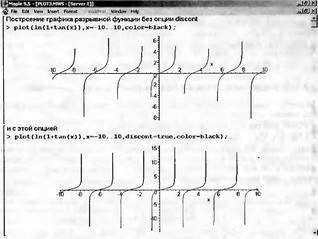

Рис. 8 2 Построение графиков функций с разрывами

Среди аргументов функции plot есть специальный параметр discont. Если задать его значение равным true, то качество графиков существенно улучшается, см. второй пример на рис. 8.2. Улучшение достигается разбиением графика на несколько участков, на которых функция непрерывна, и более тщательным контролем за отображаемым диапазоном. При discont=false данный параметр отключен и строятся обычные графики.

Следует отметить, что вид графика можно улучшить, просто задав диапазон по оси у (например, введя в параметры функции запись у=-8..10). При этом в точках разрыва могут появится вертикальные линии. Впрочем, иногда это бывает полезно.

Важное значение имеет возможность построения на одном рисунке графиков нескольких функций. В простейшем случае (рис. 8.3, первый пример) для построения таких графиков достаточно перечислить нужные функции и установить для них общие интервалы изменения.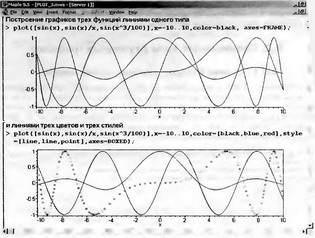

Рис. 8.3. Графики трех функций на одном рисунке

Обычно графики разных функций автоматически строятся разными цветами. Но это не всегда удовлетворяет пользователя — например, при распечатке графиков монохромным принтером некоторые кривые могут выглядеть слишком блеклыми или даже не пропечататься вообще. Используя списки параметров color (цвет линий) и style (стиль линий), можно добиться выразительного выделения кривых.

Часто возникает необходимость построения графиков функций, которые представлены просто совокупностями точек, т. е. по существу таблично.

На рис. 8.4 показано построение графиков функций по точкам при явном задании функции списком координат ее отдельных точек. В первом примере эти точки соединяются отрезками прямых, так что получается кусочно-линейный график. Видно также, что указание типа точек после указания стиля линии игнорируется (а жаль, было бы неплохо, чтобы наряду с кусочно-линейной линией графика строились и выделенные окружностями точки).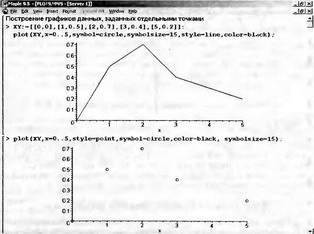

Рис. 8.4. Построение графиков функций, заданных отдельными точками

Во втором примере (рис. 8.4, снизу) показано построение только точек заданной функциональной зависимости. Они представлены маленькими кружками. Читателю предлагается самостоятельно совместить оба подхода к построению графиков по точкам и создать график в виде отрезков прямых, соединяющих заданные точки функции, представленные кружками или крестиками.

Способность Maple к упрощению работы пользователя просто поразительна — жаль только, что многие возможности этого становятся ясными после основательного изучения программы. Применительно к графикам одной из таких возможностей является построение графиков функций, заданных только их функциональными именами — даже без указания параметров в круглых скобках. Такую возможность наглядно демонстрирует рис. 8.5.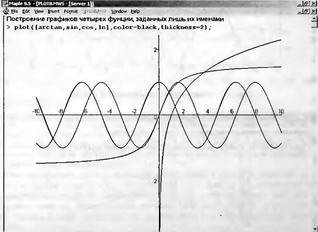

Рис. 8.5 Построение графиков четырех функций, заданных только их именами

Этот пример показывает, что возможно построение графиков функций даже без указания в команде plot диапазонов. При этом диапазон по горизонтальной оси устанавливается равным по умолчанию -8..10, а по вертикальной оси выбирается автоматически в соответствии с экстремальными значениями функций в указанном диапазоне изменения независимой переменной (условно x).

Некоторые виды функций, например, кусочные, удобно задавать процедурами. Построение графиков функций, заданных процедурами, не вызывает никаких трудностей и иллюстрируется рис. 8.6.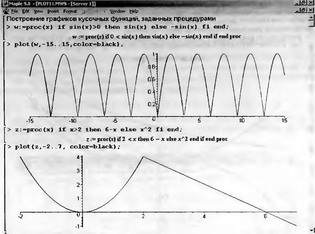

Рис. 8.6. Построение графика функций, заданных процедурами

Здесь, пожалуй, полезно обратить внимание на то, что когда в функции plot указывается имя процедуры без списка ее параметров.

Еще одна «экзотическая» возможность функции plot — построение графиков функций, заданных функциональными операторами. Она иллюстрируется рис. 8.7.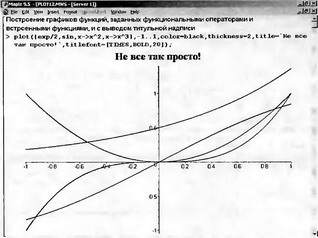

Рис. 8.7. Построение графиков функции, заданной функциональными операторами

Имена функций (без указания списка параметров в круглых скобках) тоже по существу являются функциональными операторами. Так что они также могут использоваться при построении графиков упрощенными способами.

В ряде случаев для задания функциональных зависимостей используются заданные параметрически уравнения, например x=f₁(t) и y=f₂(t) при изменении переменной t в некоторых пределах. Точки (x, y) наносятся на график в декартовой системе координат и соединяются отрезками прямых. Для этого используется функция plot в следующей форме:

plot([f1(t), f2(t), t=tmin..tmax], h, v, p)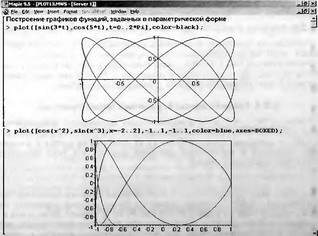

Рис. 8.8. Построение функций, заданных параметрически

Если функции f₁(t) и f₂(t) содержат периодические функции (например, тригонометрические), то для получения замкнутых фигур диапазон изменения переменной t обычно задается равным 0..2*Pi или -Pi..Pi. К примеру, если задать в качестве функций f₁(t) и f₂(t) функции sin(t) и cos(t), то будет получен график окружности. Рис. 8.8 показывает другие, чуть менее тривиальные примеры построения графиков такого рода.

Задание диапазонов для изменений h и v, а также параметров p не обязательно. Но, как и ранее, они позволяют получить вид графика, удовлетворяющий всем требованиям пользователя.

Графики в полярной системе координат представляют собой линии, которые описывает конец радиус-вектора r(t) при изменении угла t в определенных пределах — от t_min до t_max. Построение таких графиков также производится функцией plot, которая для этого записывается в следующем виде:

plot([r(t), theta(t), t=tmin..tmax], h, v, p, coords=polar)

Здесь существенным моментом является задание полярной системы координат параметр coords=polar. Рис. 8.9 дает примеры построения графиков функций в полярной системе координат.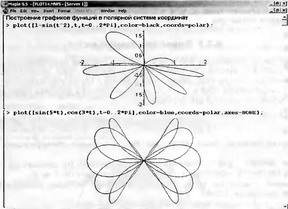

Рис. 8.9. Построение графиков функций в полярной системе координат

Графики параметрических функций и функций в полярной системе координат отличаются огромным разнообразием. Снежинки и узоры мороза на стеклах, некоторые виды кристаллов и многие иные физические объекты подчиняются математическим закономерностям, положенным в основу построения таких графиков.

Трехмерными графиками называют графики, отображающие функции двух переменных z(x, y). Каждая точка z, таких графиков является высотой (аппликатой) точки, лежащей в плоскости XY и представленной координатами (х_i, у_i). Поскольку экран монитора компьютера в первом приближении является плоским, то на деле трехмерные графики представляют собой специальные проекции объемных объектов.

Для построения графиков трехмерных поверхностей Maple имеет встроенную в ядро функцию plot3d. Она может использоваться в следующих форматах:

plot3d(expr1, x=a..b, y=c..d,p)

plot3d(f, a..b, c..d,p)

plot3d([exprf,exprg,exprh], s=a..b, t=c..d,p)

plot3d([f,g,h], a..b, c..d,p)

В двух первых формах plot3d применяется для построения обычного графика одной поверхности, в других формах — для построения графика с параметрической формой задания поверхности. В приведенных формах записи f, g и h — функции; expr1 — выражение, отражающее зависимость от х и у; exprf, exprg и exprh — выражения, задающие поверхность параметрически; s, t, а и b — числовые константы действительного типа; c и d — числовые константы или выражения действительного типа; х, у, s и t — имена независимых переменных; р — управляющие параметры.

С помощью параметров р можно в широких пределах управлять видом трехмерных графиков, выводя или убирая линии каркасной сетки, вводя функциональную окраску поверхностей, меняя угол их обзора и параметры освещения, изменяя вид координатных осей и т.д. Следующие параметры функции plot3d задаются аналогично их заданию для функции plot:

axesfont  font    color coords font      labelfcnt linestyle

numpoints scaling style symbol thickness title     titlefont

Однако функция plot3d имеет ряд дополнительных специфических параметров

• ambientlight=[r,g,b] — задает интенсивность красного (r), зеленого (g) и синего (b) цветов подсветки в относительных единицах (от 0 до 1);

• axes=f — задает вид координатных осей (BOXED, NORMAL, FRAME и NONE, по умолчанию NONE);

• grid=[m,n] — задает число линий каркаса поверхности;

• gridstyle=x — задает стиль линий каркаса х ('rectangular' или 'triangular');

• labels=[x,y,z] — задает надписи по осям (х, у и z — строки, по умолчанию пустые);

• light=[phi,theta,r,g,b] — задает углы, под которыми расположен источник освещения поверхности, и интенсивности составляющих цвета (r, g и b);

• lightmodel=x — задает схему освещения (соответственно 'none', 'light1', 'light2', 'light3' и 'light4');

• orientation=[theta,phi] — задает углы ориентации поверхности (по умолчанию 45°);

• projections — задает перспективу при обзоре поверхности (r может быть числом 0 или 1, задающим включение или выключение перспективы, а также одной из строк 'FISHEYE', 'NORMAL' или 'ORTHOGONAL' (это соответствует численным значениям r, равным 0, 0,5, или 1, причем по умолчанию задано projection=ORTHOGONAL);

• shading=s — задает направления, по которым меняется цвет функциональной окраски (значения s могут быть XYZ, XY, Z, ZGREYSCALE, ZHUE, NONE);

• tickmarks=[l,n,m] — задает характер маркировки по осям х, у и z (числа l, n и m имеют значения не менее 1);

• view=zmin..zmax или view=[xmin..xmax, ymin, ymax, zmin..zmax] — задает минимальные и максимальные координаты поверхности для ее видимых участков.

Для трехмерных графиков возможно задание множества типов координатных систем с помощью параметра coords=Тип_координатной_системы. Поскольку на экране монитора поверхность отображается только в прямоугольной системе координат и характеризуется координатами х, у и z, то для представления поверхности, заданной в иной системе координат с координатами u, v и w, используются известные формулы для преобразования (u, v, w) -> (х, у, z). Их можно найти в справке. Вид графиков трехмерных поверхностей очень сильно различается в разных координатных системах. По умолчанию трехмерные графики строятся в прямоугольной системе координат — rectangular.

На рис. 8.10 показано два примера простейших построений графиков трехмерной поверхности. По умолчанию в Maple строится поверхность с функциональной окраской и стилем style=patch (верхний рисунок) Функциональная окраска делает рисунки более информативными, но, увы, на рисунках в книге она превращается в окраску оттенками серого цвета. На рис. 8.10 показано также контекстное меню правой клавиши мыши, показывающее возможное команды, влияющие на вид трехмерных графиков.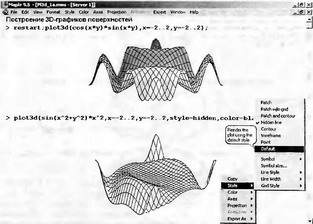

Рис. 8.10 Примеры простейшего построения трехмерных поверхностей

Параметр style=hidden строит каркасную поверхность с функциональной окраской тонких линий каркаса и удалением невидимых линий. Чтобы график выглядел более четким, построение во втором примере задано линиями черного цвета с помощью параметра color=black (см. нижний рисунок на рис. 8.10).

Помимо значения patch для построения трехмерных поверхностей можно задавать ряд других стилей: point — точками, contour — контурными линиями, line — линиями, hidden — линиями каркаса с удалением невидимых линий, wireframe — линиями каркаса со всеми видимыми линиями, patchnogrid — с раскраской, но без линий каркаса, patchcontour — раскраска с линиями равного уровня.

Цвет трехмерного графика может задаваться (как и для двумерного) параметром color=c, где с — цвет (оттенки цвета перечислялись ранее). Возможно еще два алгоритма задания цвета:

HUE — алгоритм с заданием цвета в виде color=f(x,y);

RGB — алгоритм с заданием цвета в виде color=[exprr,exprg,exprb], где выражения exprr, exprg и exprb задают относительную значимость (от 0 до 1) основных цветов (красного — exprr, зеленого — exprg и синего — exprb)

Удачный выбор углов обзора фигуры и применение функциональной окраски позволяют придать построениям трехмерных фигур весьма эффектный и реалистический вид.

Как отмечалось, вид графика трехмерной поверхности существенно зависит от выбора координатной системы. Рис. 8.11 показывает пример построения нелинейного конуса в цилиндрической системе координат. Для задания такой системы координат используется параметр coords=cylindrical.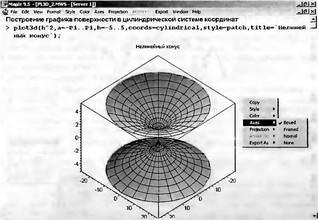

Рис. 8.11. Нелинейная цилиндрическая поверхность

При построении этой фигуры также использована цветная функциональная окраска. Кроме того, этот пример иллюстрирует вывод над рисунком титульной надписи (кстати, сделанной на русском языке).

Приведем еще один пример построения трехмерной поверхности — на этот раз в сферической системе координат (рис. 8.12). Здесь функция задана вообще элементарно просто — в виде числа 1. Но, поскольку выбрана сферическая система координат, в результате строится поверхность шара единичного радиуса. Обратите внимание на возможность построения только части сферы за счет ограничения изменения переменных координатной системы.

Рис. 8.12. Построение шарообразной поверхности в сферическом системе координат

Полезно просмотреть построение графиков в различных системах координат. При этом можно получить самые необычные фигуры.

На рис. 8.13 показано построение простого тороида — цилиндра, свернутого в кольцо. Здесь также использован прием удаления части фигуры, что делает ее представление более наглядным и красочным. Кроме того, введены параметры, задающие функциональную окраску.

Рисунок 8.13 дает полное и наглядное представление об этой фигуре — причем не только снаружи, но и изнутри.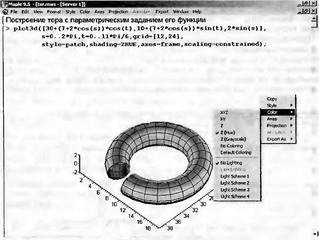

Рис. 8.13. Тор с функциональной окраской поверхности

Полезно обратить внимание на параметр масштаба scaling=constrained, явно введенную в документ рис. 8.13. Ее можно было бы и не вводить, поскольку этот параметр изначально задается по умолчанию. Она выравнивает масштабы представления фигуры по осям координат, обычно используется по умолчанию и позволяет снизить до минимума геометрические искажения фигур — тор, например, при этом виден как круглая труба, свернутая в кольцо. У таких графиков есть специфический недостаток — они занимают малую часть окна вывода.

Задание параметра scaling=unconstrained означает отказ от равного масштаба по осям. График при этом увеличивается в размерах, но становятся заметны его искажения по осям координат. В итоге он тор превращается в толстую сплющенную трубу с эллиптическим сечением (рис. 8.14).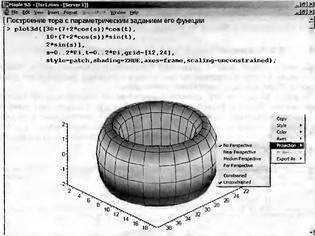

Рис. 8.14. Тор, построенный с применением значения параметра scaling=unconstrained

Весьма важным является учет углов, под которыми наблюдается трехмерная поверхность или объект. К примеру, построение рис. 8.14 неудачно в том плане, что оно не показывает наличия у тора дырки. Простейший и очень удобный способ изменить угол обзора заключается во вращении фигуры на рисунке мышью при нажатой левой кнопке. При этом можно повернуть фигуру так, что ее геометрические особенности будут отчетливо видны. Попробуйте проделать это.

В Maple есть способ явно задать углы обзора с помощью параметра orientation=[theta, phi], где theta и phi — углы, через которые задаются параметрические уравнения трехмерной фигуры или поверхности. Рисунок 8.15 дает пример такого задания фигуры, которую можно назвать «квадратным» тором.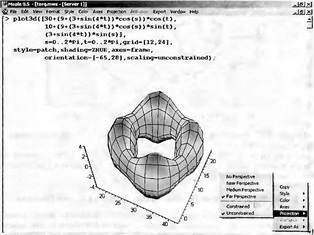

Рис. 8.15. «Квадратный» тор, представленный под заданными углами обзора

Обратите внимание, что значения заданных углов обзора повторяются в полях углов на контекстной панели инструментов. Разумеется, последние будут меняться, если начать вращать фигуру на рисунке мышью.

Параметрическое задание уравнений поверхности открывает почти неисчерпаемые возможности построения занимательных и сложных фигур самого различного вида. Приведем пару построений такого рода.

На рис. 8.16 показан тор, сечение которого имеет вид сплюснутой шестиконечной звезды. Вырез в фигуре дает прекрасный обзор ее внутренней поверхности, а цветная функциональная окраска и линии сетки, построенные с применением алгоритма удаления невидимых линий, дают весьма реалистичный вид фигуры. Замените параметр scaling=unconstrained на scaling=constrained, и вы получите тор с неискаженным сечением.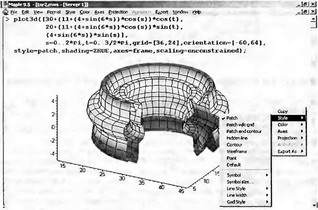

Рис. 8 16. Тор с сечением в виде шестиконечной звезды

На рис. 8.17 показан еще один тор. На этот раз он круглого сечения, но сверху к снизу имеет вид пятиконечной звезды.

Рис. 8.17. Тор круглого сечения в виде пятиконечной звезды

Быстрое (не в смысле ускорения самого построения, а лишь в смысле более быстрою задания построения графиков) построение трехмерных графиков обеспечивает функция smartplot3d.

Функция plot3d позволяет строить одновременно несколько фигур, пересекающихся в пространстве. Для этого достаточно вместо описания одной поверхности задать список описаний ряда поверхностей. При этом функция plot3d обладает уникальной возможностью — автоматически вычисляет точки пересечения фигур и показывает только видимые части поверхностей. Это создает изображения, выглядящие вполне естественно. Пример такого построения для двух функций показан на рис. 8.18.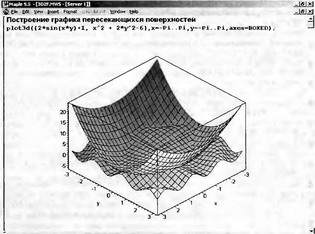

Рис. 8.18. Пример построения двух трехмерных фигур, пересекающихся в пространстве

Функции PLOT и PLOT3D (с именами, набранными большими буквами) позволяют создавать графические структуры, содержащие ряд графических объектов s1, s2, s3 и т.д. Каждый объект может представлять собой точку или фигуру, полигон, надпись и т.д., позиционированную с высокой точностью в заданной системе координат. Координатные оси также относятся к графическим объектам. Важно отметить, что функции PLOT и PLOT3D одновременно являются данными, описывающими графики. Их можно записывать в виде файлов и (после открытия файлов) представлять в виде графиков. Особые свойства этих функций подчеркиваются их записью прописными буквами.

Графическая структура двумерной графики задается в виде

PLOT(s1, s2, s3,...,о);

где s1, s2, s3 … — графические объекты (или элементарные структуры — примитивы), о — общие для структуры параметры).

Основными объектами являются:

• POINTS([x1,y1],[x2,y2],…[xn,yn]) — построение точек, заданных их координатами;

• CURVES([[x11,y11],…[x1n,y1n]], [[x21,y21],…[x2n,y2n]],… [[xm1,ym1],…[xmn,ymn]]) — построение кривых по точкам;

• POLYGONS([[x11,у11],…[х1n,y1n]], [[х21,у21],…[х2n,у2n]],…[[xm1,ym1],…[xmn,ymn]]) — построение замкнутой области-полигона (многоугольника, так как последняя точка должна совпадать с первой);

• ТЕХТ([х,у],`string`,horizontal,vertical) — вывод текстовой надписи `string`, позиционированной в точке с координатами [х,у], с горизонтальной или вертикальной ориентацией. Параметр horizontal может иметь значения ALIGNLEFT или ALIGNRIGHT, указывающие, в какую сторону (влево или вправо) идет надпись. Аналогично, параметр vertical может иметь значения ALIGNABOVE или ALIGNBELOW, указывающие в каком направлении (вверх или вниз) идет надпись.

При задании графических объектов (структур) s1, s2, s3 и т.д. можно использовать описанные выше параметры и параметры, например, для задания стиля построения - STYLE (POINT, LINE, PATCH, PATCHNOGRID); толщины линий — THICKNESS (кроме координатных осей); символа, которым строятся точки кривых — SYMBOL (BOX, CROSS, CIRCLE, POINT, DIAMOND и DEFAULT); стиля линий — LINESTYLE; цвета — COLOR (например, COLOR(HUE,0) для закраски непрерывной области), типа шрифта — FONT; вывода титульной надписи — TITLE(string); имени объекта — NAME(string); стиля координатных осей — AXESSTYLE (BOX, FRAME, NORMAL, NONE или DEFAULT) и т.д.

Следует отметить, что параметры в графических структурах задаются несколько иначе — с помощью круглых скобок. Например, для задания шрифта TIMES ROMAN с размером символов 16 пунктов надо записать FONT(TIMES, ROMAN, 16), для задания стиля координатных осей в виде прямоугольника — AXES-STYLE (BOX) и т.д.

На рис. 8.19 показан пример графических построений при использовании основных структур двумерной графики.

Рис. 8.19. Пример использования двумерных структур

Как видно из этого примера, графическая двумерная структура позволяет задавать практически любые двумерные графики и текстовые надписи в пределах одного рисунка.

Графические структуры трехмерной графики строятся функцией PLOT3D:

PLOT3D(s1,s2,s3,...,о)

В качестве элементарных графических структур можно использовать уже описанные выше объекты POINTS, CURVES, POLYGONS и TEXT — разумеется, с добавлением в списки параметров третьей координаты. Пример такого построения дан на рис. 8.20.

Рис 8.20 Пример создания структуры трехмерной графики

Кроме того, могут использоваться некоторые специальные трехмерные структуры. Одна из них — структура GRID:

GRID(a..b,c..d,listlist) — задание поверхности над участком координатной плоскости, ограниченной отрезками [a, b] и [с, d], по данным, заданным переменной-списком listlist:=[[z11,…z1n], [z21,…z2n],…[zm1…zmn]] с размерностью n×m. Заметим, что эта переменная задает координату z для равноотстоящих точек поверхности.

На рис. 8.21 показан пример создания структуры трехмерной графики на базе GRID. Изображение представляет собой линии, соединяющие заданные точки.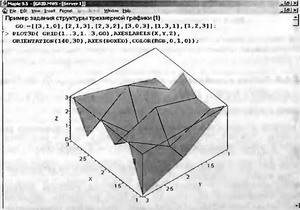

Рис. 8.21. Пример задания графической структуры типа GRID

Еще один тип трехмерной графической структуры — это MESH:

MESH(listlist) — задание трехмерной поверхности по данным списочной переменной listlist, содержащей полные координаты всех точек поверхности (возможно задание последней при неравномерной сетке).

Обычная форма задания этой структуры следующая:

MESH([[[x11, y11, z11], ... [x1n, y1n, z1n]], [[x21, у21, z21], ... [x2n, y2n, z2n]], ... [[xm1, ym1, zm1] ... [xmn, ymn, zmn}]])

Пример задания такой структуры представлен на рис. 8.22.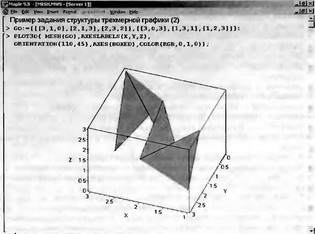

Рис. 8.22. Пример задания графической структуры типа MESH

Описанные структуры могут использоваться и в программных модулях. Много таких примеров описано в книгах, поставляемых с системой Maple.

Пакет plots содержит почти полсотни графических функций, существенно расширяющих возможности построения двумерных и трехмерных графиков в Maple:

> with(plots);

Warning, the name changecoords has been redefined

Ввиду важности этого пакета отметим назначение всех его функций:

• animate — создает анимацию двумерных графиков функций;

• animate3d — создает анимацию трехмерных графиков функций;

• animatecurve — создает анимацию кривых;

• changecoords — смена системы координат;

• complexplot — построение двумерного графика на комплексной плоскости;

• complexplot3d — построение трехмерного графика в комплексном пространстве;

• conformal — конформный график комплексной функции;

• contourplot — построение контурного графика,

• contourplot3d — построение трехмерного контурного графика;

• coordplot — построение координатной системы двумерных графиков;

• coordplot3d — построение координатной системы трехмерных графиков;

• cylinderplot — построение графика поверхности в цилиндрических координатах;

• densityplot — построение двумерного графика плотности;

• display — построение графика для списка графических объектов;

• display3d — построение графика для списка трехмерных графических объектов;

• fieldplot — построение графика двумерного векторного поля;

• fieldplot3d — построение графика трехмерного векторного поля;

• gradplot — построение графика двумерного векторного поля градиента;

• gradplot3d — построение графика трехмерного векторного поля градиента;

• implicitplot — построение двумерного графика неявной функции;

• implicitplot3d — построение трехмерного графика неявной функции;

• inequal — построение графика решения системы неравенств;

• listcontplot — построение двумерного контурного графика для сетки значений;

• listcontplot3d — построение трехмерного контурного графика для сетки значений;

• listdensityplot — построение двумерного графика плотности для сетки значений;

• listplot — построение двумерного графика для списка значений:

• listplot3d — построение трехмерного графика для списка значений;

• loglogplot — построение логарифмического двумерного графика функции;

• logplot — построение полулогарифмического двумерного графика функции;

• matrixplot — построение трехмерного графика со значениями Z, определенными матрицей;

• odeplot — построение двумерного или трехмерного графика решения дифференциальных уравнений;

• pareto — построение диаграммы (гистограммы и графика линиями);

• pointplot — построение точками двумерного графика;

• pointplot3d — построение точками трехмерного графика;

• polarplot — построение графика двумерной кривой в полярной системе координат;

• polygonplot — построение графика одного или нескольких многоугольников с вершинами, задаваемыми списками их координат;

• polygonplot3d — построение одного или нескольких многоугольников в пространстве;

• polyhedraplot — построение трехмерного многогранника;

• replot — перестроение графика заново;

• rootlocus — построение графика корней уравнения с комплексными неизвестными;

• semilogplot — построение графика функции с логарифмическим масштабом по оси абсцисс;

• setoptions — установка параметров по умолчанию для двумерных графиков;

• setoptions3d — установка параметров по умолчанию для трехмерных графиков;

• spacecurve — построение трехмерных кривых;

• sparsematrixplot — построение двумерного графика, отличных от нуля значений матрицы;

• sphereplot — построение графика трехмерной поверхности в сферических координатах;

• surfdata — построение трехмерного графика поверхности по численным данным;

• textplot — вывод текста на заданное место двумерного графика;

• textplot3d — вывод текста на заданное место трехмерного графика;

• tubeplot — построение трехмерного графика типа «трубы».

Среди этих функций надо отметить, прежде всего, средства построения графиков ряда новых типов (например, графиков в комплексной плоскости, в виде линий равного уровня, векторных полей и т.д.), а также средства объединения различных графиков в один. Особый интерес представляют две первые функции, обеспечивающие анимацию как двумерных (animate), так и трехмерных графиков (animate3d). Этот пакет вполне заслуживает описания в отдельной книге. Но, учитывая ограниченный объем данной книги, мы рассмотрим лишь несколько характерных примеров его применения. Заметим, что для использования приведенных функций нужен вызов пакета, например, командой with(plots)

В пакете plots есть функция для построения двумерных (2D) графиков в полярной системе координат. Она имеет вид polarplot(L,o), где L — объекты для задания функции, график которой строится, и о — необязательные параметры. На рис. 8.23 сверху представлен пример построения графика с помощью функции polarplot.

Рис. 8.23. Графики, построенные с помощью функций polarplot и implicitplot

В первом примере для большей выразительности опущено построение координатных осей, а график выведен линией удвоенной толщины. График очень напоминает лист клена, весьма почитаемого в Канаде и ставшего эмблемой СКМ Maple.

В математике часто встречается особый тип задания геометрических фигур, при котором переменные х и у связаны неявной зависимостью. Например, окружность задается выражениемх²+y²=R², где R — радиус окружности. Для задания двумерного графика такого вида служит функция импликативной графики:

implicitplot(eqn,х=а..b,у=с..d,options)

Пример построения окружности с помощью этой функции показан на рис. 8.23 снизу. Ниже мы рассмотрим подобную функцию и для трехмерного графика.

Графики, построенные с помощью линий равного уровня (их также называют контурными графиками) часто используются в картографии. Эти графики получаются, если мысленно провести через трехмерную поверхность ряд равноотстоящих плоскостей, параллельных плоскости, образованной осями X и Y графика. Линии равных высот образуются в результате пересечения этих плоскостей с трехмерной поверхностью.

Для построения таких графиков используется функция contourplot, которая может использоваться в нескольких форматах:

contourplot(expr1, х=а..b, у=с..d)

contourplot(f,a..b,c..d)

contourplot([exprf,exprg,exprh],s=a..b,t=c..d)

contourplot([f,g,h],a..b,c..d)

contourplot3d(expr1,x=a..b,y=c..d)

contourplot3d(f,a..b,c..d)

contcurplot3d([exprf, exprg, exprh], s=a..b, t=c..d)

contourplot3d([f,g,h],a..b,c..d)

Здесь f, g и h — функции; expr1 — выражение, описывающее зависимость высоты поверхности от координат x и y: exprf, exprg и exprh — выражения, зависящие от s и t, описывающие поверхность в параметрической форме; а и b — константы вещественного типа; c и d — константы или выражения вещественного типа; х, у, s и t — имена независимых переменных.

На рис. 8.24 показано построение графика линиями равного уровня для одной функции. Параметр filled=true обеспечивает автоматическую функциональную окраску замкнутых фигур, образованных линиями равного уровня. Порою это придает графику большую выразительность, чем при построении только линии равного уровня.

Рис. 8.24. Пример построения графика функции линиями равного уровня

К сожалению, в данном варианте окраски сами контурные линии получаются черными и их невозможно отличить. Однако если убрать параметр filled=true, то контурные линии (и линии легенды) будут иметь разный цвет и легко различаться. Оцифровка линий контурного графика, увы, не предусмотрена.

Функция contourplot позволяет строить и графики ряда функции. Пример такого построения показан на рис. 8.25. Множество окружностей на этом рисунке создается четырьмя поверхностями, заданными функциями с1, с2, c3 и с4.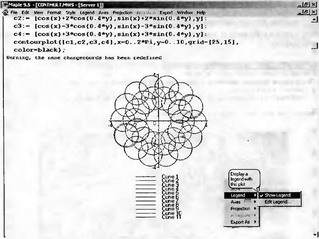

Рис. 8.25. Пример построения графиков многих функций линиями равного уровня

Обратите внимание, что на многих графиках Maple по умолчанию вписывает легенду, то есть список линий с обозначениями. Иногда (как, например, на рис. 8.25), этот список оказывается просто некстати. Легенду можно убрать, расширив заодно место для графика, сняв флажок Show Legend в контекстном меню Legend правой клавиши мыши (это меню видно на рис. 8.25). Заодно запомните, что легенду можно редактировать, выполнив команду Edit Legend.

Следует отметить, что хотя графики в виде линий равного уровня выглядят не так эстетично и естественно, как обычные графики трехмерных поверхностей (ибо требуют осмысления результатов), у них есть один существенный плюс — экстремумы функций на таких графиках выявляются порой более четко, чем на обычных графиках. Например, небольшая возвышенность или впадина за большой «горой» на обычном графике может оказаться невидимой, поскольку заслоняется «горой». На графике линий равного уровня этого эффекта нет. Однако выразительность таких графиков сильно зависит от числа контурных линий.

Иногда поверхности отображаются на плоскости как графики плотности — чем выше высота поверхности, тем плотнее (темнее) окраска. Такой вид графиков создается функцией densityplot. Она может записываться в двух форматах:

densityplot(expr1, х=а..b,у=с..d)

densityplot(f,a..b,c..d)

где назначение параметров соответствует указанному выше для функции contourplot.

На рис. 8.26 (верхняя часть) дан пример построения графика такого типа. Нетрудно заметить, что в плоскости XY график разбит на квадраты, плотность окраски которых различна. В нашем случае плотность окраски задается оттенками серого цвета.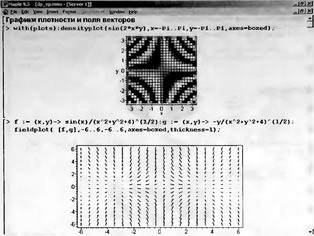

Рис. 8.26. Графики плотности и поля векторов

Обычно графики такого типа не очень выразительны, но имеют свои области применения. К примеру, оттенки окраски полупрозрачной жидкости могут указывать на рельеф поверхности дна емкости, в которой находится эта жидкость.

Еще один распространенный способ представления трехмерных поверхностей — графики полей векторов. Они часто применяются для отображения полей, например электрических зарядов. Особенность таких графиков в том, что для их построения используют стрелки, направление которых соответствует направлению изменения градиента поля, а длина — значению градиента. Так что термин «поле векторов» надо понимать в смысле, что поле графика заполнено векторами.

Для построения таких графиков в двумерной системе координат используется функция fieldplot:

fieldplot(f, r1, r2)

fieldplot(f, r1, r2, ...)

где f — вектор или множество векторов, задающих построение; r1 и r2 — пределы.

На рис. 8.26 в нижней части документа показан вид одного из таких графиков. Следует отметить, что для получения достаточного числа отчетливо видных стрелок надо поработать с форматированием графиков. Иначе графики этого типа могут оказаться не очень представительными. Так, слишком короткие стрелки превращаются в черточки и даже точки, не имеющие острия, что лишает графики наглядности.

Трехмерные поверхности также могут задаваться уравнениями неявного вида. В этом случае для построения их графиков используется функция implicitplot3d:

implicitplot3d(expr1,х=а..b,y=c..d,z=p..q,<options>)

implicitplot3d(f,a..b,c..d,p..q, <options>)

На рис. 8.27 показаны два примера построения любопытных объемных фигур с помощью функции implicitplot3d.

Рис. 8.27. Примеры применения функции implicitplot3d

Эти примеры, взятые из справки, хорошо иллюстрируют технику применения функции implicitplot3d. С ее помощью можно строить весьма своеобразные фигуры, что, впрочем, видно и из приведенных примеров. Для наглядности фигур рис. 8.40 они несколько развернуты в пространстве с помощью мыши.

В пакете plots имеется множество функций для построения графиков в различных системах координат Объем книги не позволяет воспроизвести примеры всех видов таких графиков, ибо их многие сотни. Да это и не надо — во встроенных в справочную систему примерах можно найти все нужные сведения. Так что ограничимся лишь парой примеров применения функции tubeplot(C, options), позволяющей строить весьма наглядные фигуры в пространстве, напоминающие трубы или иные объекты, образованные фигурами вращения.

На рис. 8.28 показана одна из таких фигур. Она поразительно напоминает раковину улитки. Функциональная окраска достигнута доработкой графика с помощью панели форматирования — она, как и контекстное меню правой клавиши мыши, показана на рис. 8.28.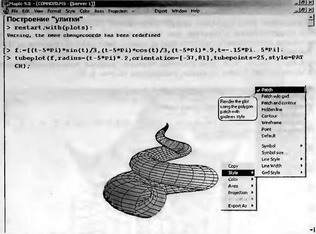

Рис. 8.28. Построение графика — «раковина улитки»

Эта функция может использоваться и для построения ряда трубчатых объектов в пространстве. При этом автоматически задается алгоритм удаления невидимых линий даже для достаточно сложных фигур. Это наглядно иллюстрирует пример на рис. 8.29, показывающий фигуру «цепи». Не правда ли, реалистичность этой фигуры поражает воображение?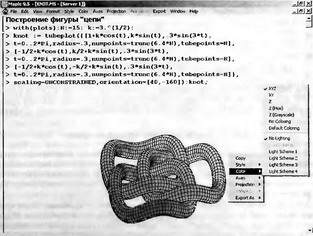

Рис. 8.29. Фигура «цепи», построенная с применением функции tubeplot

Можно долго размышлять о том, как те или иные математические закономерности описывают предметы реального мира, положенные в основу тех или иных геометрических объектов или, возможно, о гениальности людей, сумевших найти такие закономерности для многих из таких объектов. В наше время Maple открывает огромные возможности для таких людей.

Наглядность ряда графиков можно существенно увеличить, строя их в трехмерном представлении. Например, для такого построения графиков полей из векторов можно использовать графическую функцию fieldplot3d. В отличие от функции fieldplot она строит стрелки как бы в трехмерном пространстве (рис. 8.30). Возможности смены осей о оформления «ящика» графика иллюстрирует контекстное меню правой клавиши мыши, показанное на рис. 8.30.

Рис. 8.30. Построение поля в трехмерном пространстве с помощью векторов

Все сказанное об особенностях таких двумерных графиков остается справедливым и для графиков трехмерных. В частности, для обеспечения достаточной наглядности нужно тщательно отлаживать форматы представления таких графиков.

В отличие от векторных графиков, контурные графики поверхностей, наложенные на сами эти поверхности, нередко повышают восприимчивость таких поверхностей — подобно изображению линий каркаса. Для одновременного построения поверхности и контурных линий на них служит функция contourplot3d. Пример ее применения показан на рис. 8.31.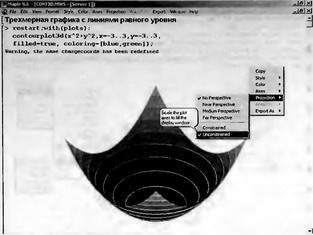

Рис. 8.31. График поверхности с контурными линиями

Для повышения наглядности этот график доработан с помощью контекстной панели инструментов графиков. В частности, включена функциональная окраска и подобраны углы обзора фигуры, при которых отчетливо видны ее впадина и пик. О возможностях переформатирования графика свидетельствует контекстное меню, показанное на рис. 8.31.

Приведенные выше достаточно простые примеры дают представление о высоком качестве визуализации геометрических фигур с помощью пакета plots. Здесь мы рассмотрим еще несколько примеров визуализации трехмерных фигур. Многие видели катушки индуктивности, у которых провод того или иного диаметра намотан на тороидальный магнитный сердечник. Некую математическую абстракцию такой катушки иллюстрирует рис. 8.32.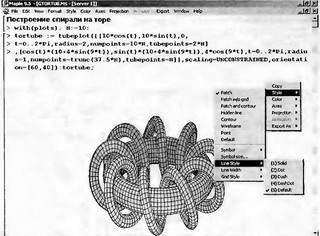

Рис. 8.32. Тор с обмоткой — толстой спиралью

В документе рис. 8.32 для функции tubeplot использовано довольно большое число параметров. Не всегда их действие очевидно. Поэтому на рис. 8.33 показано показано построение тора с тонкой обмоткой. Здесь также показано меню правой клавиши мыши, позволяющее менять стиль построения графика. Можно также поэкспериментировать с управляющими параметрами графика, от которых сильно зависят его представительность и наглядность.

Рис. 8.33. Тор с тонкой обмоткой

В ряде случаев наглядно представленные фигуры можно строить путем объединения однотипных фигур. Пример графика подобного рода представлен на рис. 8.34. Здесь готовится список графических объектов s, смещенных по вертикали. С помощью функции display они воспроизводятся на одном графике, что повышает реалистичность изображения.

Рис. 8.34. Построение фигуры, напоминающей шину автомобиля

Последний пример имеет еще одну важную особенность — он иллюстрирует задание графической процедуры, в теле которой используются функции пакета plots. Параметр n этой процедуры задает число элементарных фигур, из которых строится полная фигура. Таким образом, высотой фигуры (или шириной «шины») можно управлять. Возможность задания практически любых графических процедур средствами Maple-языка существенно расширяет возможности Maple.

Наглядность таких графикой, как графики плотности и векторных полей может быть улучшена их совместным применением. Такой пример показан на рис. 8.35.

Рис. 8.35. Пример совместного применения графиков плотности и векторного поля

Этот пример иллюстрирует использование «жирных» стрелок для обозначения векторного поля. Наглядность графика повышается благодаря наложению стрелок на график плотности, который лучше, чем собственно стрелки, дает представление о плавности изменения высоты поверхности, заданной функцией f.

В пакет Plots СКМ Maple 9.5 введена новая функция для сравнения двух зависимостей f(z) и g(z) комплексного аргумента z. Функция может использоваться в нескольких формах:

plotcompare(f(z), g(z), z = a+c*I..b+d*I, options);

plotcompare(f(z) = g(z), ...);

plotcompare(f, g, a+c* I..b+d*I, options);

plotcompare(f=g, ...);

Здесь a, b, c, d - константы реального типа. Функция на одном рисунке строит графики действительной и мнимой частей зависимостей f(z) и g(z). С помощью опций можно менять цветовую гамму рисунков, их ориентацию в пространстве и др. характеристики графиков. В справке по данной функции дается множестве примеров ее применения, так что ограничимся одним, показанным на рис. 8.36.

Рис. 8.16. Пример графического сопоставления двух зависимостей от комплексного аргумента

Сравнение графиков двух зависимостей, представленных на рис. 8.36 наглядно выявляет существенные отличия этих зависимостей. Достаточно отметить, что на графиках действительных частей зависимостей в одном случае видна выпуклая, а в другом случае вогнутая поверхности. Еще сильнее отличия в графиках мнимых частей сопоставляемых зависимостей.

Визуализация графических построений и результатов моделирования различных объектов и явлений существенно повышается при использовании средств «оживления» (анимации) изображений. Пакет plots имеет две простые функции для создания динамических (анимированных) графиков.

Первая из этих функций служит для создания анимации графиков, представляющих функцию одной переменной F(x):

animatecurve(F, r, ...)

Эта функция просто позволяет наблюдать медленное построение графика. Формат ее применения подобен используемому в функции plot.

При вызове данной функции вначале строится пустой шаблон графика. Если активизировать шаблон мышью, то в строке главного меню появляется меню Animation. Меню Animation содержит команды управления анимацией. Такое же подменю появляется и в контекстном (рис. 8.37).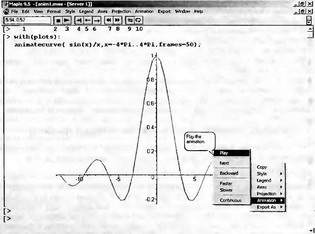

Рис. 8.37. Пример анимационного построения графика функцией animatecurve

Указанное подменю содержит следующие команды анимации:

• Play — запуск построения графика;

• Next — выполнение следующего шага анимации;

• Backward/Forward — переключение направления анимации (назад/вперед);

• Faster — ускорение анимации;

• Slower — замедление анимации;

• Continiuus/Single cycle — цикличность анимации.

При исполнении команды Play происходит построение кривой (или нескольких кривых). В зависимости от выбора команд Faster или Slower построение идет быстро или медленно. Команда Next выполняет один шаг анимации — построение очередного фрагмента кривой. Переключатель Backward/Forward позволяет задать направление построения кривой — от начала к концу или от конца к началу. Построение может быть непрерывным или циклическим в зависимости от состояния позиции Continiuus/Single cycle в подменю управления анимацией. При циклической анимации число циклов задается параметром frames=n.

При включенном выводе панели форматирования во время анимации она приобретает вид панели проигрывателя клипов (рис. 8.37). Эта панель имеет кнопки управления с обозначениями, принятыми у современных проигрывателей, например магнитофонов

1. Поле координат перемещающейся точки графика.

2. Остановка анимации

3. Пуск анимации

4. Переход к следующему кадру (фрейму).

5. Установка направления анимации от конца в начало.

6. Установка направления анимации из начала в конец (по умолчанию).

7. Уменьшение времени шага анимации.

8. Увеличение времени шага анимации.

9. Установка одиночного цикла анимации.

10. Установка серии циклов анимации.

Итак, кнопки проигрывателя по существу повторяют команды подменю управления анимацией.

Нажав кнопку пуска (с треугольником, острием обращенным вправо), можно наблюдать изменение вида кривой для функции sin(х)/(х). Другие кнопки управляют характером анимации. Проигрыватель дает удобные средства для демонстрации анимации, например, во время занятий со школьниками или студентами.

Более обширные возможности анимации двумерных графиков обеспечивает функция animate:

animate(F, х, t)

animate(F, x, t, o)

В ней параметр x задает пределы изменения переменной х, а параметр t — пределы изменения дополнительной переменной t. Суть анимации при использовании данной функции заключается в построении серии кадров (как в мультфильме), причем каждый кадр связан со значением изменяемой во времени переменной t. Если надо явно задать число кадров анимации N, то в качестве о следует использовать frame=N.

Рисунок 8.38 показывает применение функции animate.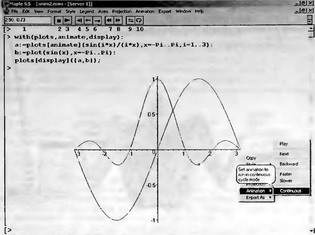

Рис. 8.38. Анимация функции sin(i*x)/(i*x) на фоне неподвижной синусоиды

В документе рис. 8.38 строятся две функции — не создающая анимации функция sin(x) и создающая анимацию функция sin(i*x)/(i*x), причем в качестве переменной t задана переменная i. Именно ее изменение и создает эффект анимации. Проигрыватель анимационных клипов и меню, описанные выше, могут использоваться для управления и этим видом анимации. Обратите внимание на вызов графических функций в этом примере командой with и на синтаксис записи этих функций.

К сожалению, картинки в книгах всегда неподвижны и воспроизвести эффект анимации невозможно. Можно лишь представить несколько текущих кадров анимации. Представленная на рис. 8.38 картина соответствует последнему кадру анимации.

Анимация графиков может найти самое широкое применение при создании учебных материалов. С ее помощью можно акцентировать внимание на отдельных параметрах графиков и образующих их функций и наглядно иллюстрировать характер их изменений.

Аналогичным образом может осуществляться и анимация трехмерных фигур. Для этого используется функция animate3d:

animate3d(F,х,у,t,o)

Здесь F — описание функции (или функций); х, у и t — диапазоны изменения переменных х, у и t. Для задания числа кадров N надо использовать необязательный параметр о в виде frame=N. Примеры применения этой функции мы рассмотрим позже.

На рис. 8.39 показано построение графика с анимацией. После задания функции, график которой строится, необходимо выделить график и запустить проигрыватель, как это описывалось для анимации двумерных графиков.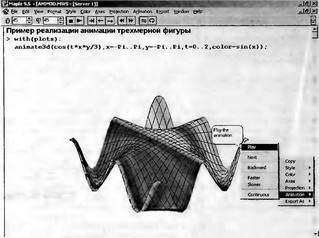

Рис. 8.39. Подготовка трехмерного анимационного графика

На рис. 8.39 показано также контекстное меню поля выделенного графика. Нетрудно заметить, что с помощью этого меню (и содержащихся в нем подменю) можно получить доступ к параметрам трехмерной графики и выполнить необходимые операции форматирования, такие как включение цветовой окраски, выбор ориентации фигуры и т.д.

Назначение параметров, как и средств управления проигрывателем анимационных клипов, было описано выше.

Еще один путь получения анимационных рисунков — создание ряда графических объектов p1, p2, p3 и т.д. и их последовательный вывод с помощью функций display или display3d:

display(p1,p2,р3,..nsequence=true)

display3d(p1,p2,p3...,insequence=true)

Здесь основным моментом является применение параметра insequence=true. Именно он обеспечивает вывод одного за другим серии графических объектов р1, р2, p3 и т.д. При этом объекты появляются по одному, и каждый предшествующий объект стирается перед появлением нового объекта. Этот метод анимации мы рассмотрим чуть позже.

Инструментальный пакет графики plottools служит для создания графических примитивов, строящих элементарные геометрические объекты на плоскости и в пространстве: отрезки прямых и дуг, окружности, конусы, кубики и т.д. Его применение позволяет разнообразить графические построения и строить множество графиков специального назначения. В пакет входят следующие графические примитивы:

arc          arrow       circle      cone       cuboid

curve        cutin       cutout      cylinder   disk

dodecahedron ellipse     ellipticArc hemisphere hexahedron

hyperbola    icosahedron line        octahedron pieslice

point        polygon     rectangle   semitorus  sphere

tetrahedron  torus

Вызов перечисленных примитивов осуществляется после загрузки пакета в память компьютера командой with(plottools). Только после этого примитивы пакета становятся доступными. Обычно примитивы используются для задания графических объектов, которые затем выводятся функцией display. Возможно применение этих примитивов совместно с различными графиками.

Большинство примитивов пакета plottools имеет довольно очевидный синтаксис. Например, для задания дуги используется примитив arc(c, r, а..b,…), где с — список с координатами центра окружности, к которой принадлежит дуга, r — радиус этой окружности, а..b — диапазон углов. На месте многоточия могут стоять обычные параметры, задающие цвет дуги, толщину ее линии и т.д. Конус строится примитивом cone(c,r,h…), где с — список с координатами центра, r — радиус основания, h — высота и т.д. В необходимых случаях стоит проверить синтаксис того или иного примитива с помощью справки по пакету plottools.

На рис. 8.40 показано применение нескольких примитивов двумерной графики для построения дуги, окружности, закрашенного красным цветом эллипса и отрезка прямой. Кроме того, на графике показано построение синусоиды.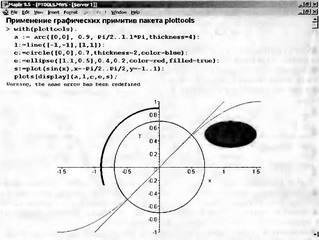

Рис. 8.40 Примеры применения примитивов двумерной графики пакета plottools

Во избежание искажений пропорций фигур надо согласовывать диапазон изменения переменной x. Обычно параметр scalling=constrained выравнивает масштабы и диапазоны по осям координат, что гарантирует отсутствие искажений у окружностей и других геометрических фигур. Однако при этом размеры графика нередко оказываются малыми. Напоминаем, что эту параметр можно задать и с помощью подменю Projection.

Рис. 8.41 иллюстрирует построение средствами пакета plottools четырех разноцветных стрелок, направленных в разные стороны. Цвет стрелок задан списком цветов с, определенным после команды загрузки пакета. Для построения стрелок используется примитив arrow с соответствующими параметрами. Обратите внимание на наклон стрелок — он задан прибавлением 1 к аргументу тригонометрических функций. Уберите 1 и стрелки расположатся под прямым углом.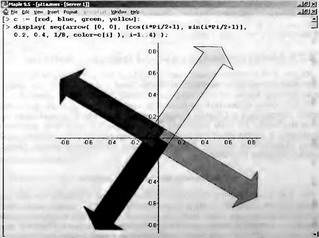

Рис. 8.41. Построение разноцветных стрелок, направленных в разные стороны

Примитивы могут использоваться в составе графических процедур, что позволяет конструировать практически любые типы сложных графических объектов. В качестве примера на рис. 8.42 представлена процедура SmithChart, которая строит хорошо известную электрикам диаграмму Смита (впрочем, несколько упрощенную). В этой процедуре используется примитив построения дуг arc. При этом задается верхняя часть диаграммы, а нижняя получается ее зеркальным отражением.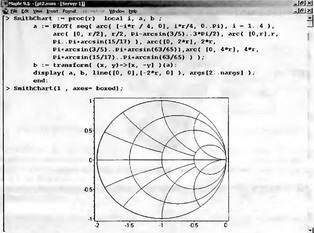

Рис. 8.42. Построение диаграммы Смита

Обратите внимание на то, что начиная с рис. 8.42 мы не указываем загрузку пакета plottools, поскольку она уже была проведена ранее. Однако надо помнить, что все примеры этого раздела предполагают, что такая загрузка обеспечена. Если вы использовали команду restart или только что загрузили систему Maple 9 то для исполнения примера рис. 8.42 и последующих примеров надо исполнить команду with(plottools).

Аналогичным описанному выше образом используются примитивы построения трехмерных фигур. Это открывает возможность создания разнообразных иллюстрационных рисунков и графиков, часто применяемых при изучении курса стереометрии. Могут строиться самые различные объемные фигуры и поверхности — конусы, цилиндры, кубы, полиэдры и т.д. Использование средств функциональной окраски делает изображения очень реалистичными.

Рис. 8.43 показывает построение цилиндра и двух граненых шаров. Цилиндр строится примитивом cylinder, а граненые шары — примитивом icosahedron.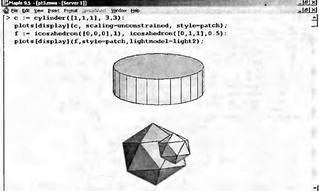

Рис. 8.43. Построение цилиндра и двух граненых шаров

Другой пример (рис. 8.44) иллюстрирует построение на одном графике двух объемных фигур, одна из которых находится внутри другой фигуры. Этот пример демонстрирует достаточно корректное построение вложенных фигур.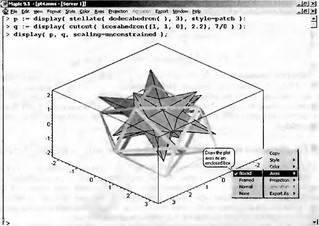

Рис. 8.44. Построение двух объемных фигур

На рис. 8.45 показано совместное построение двух пересекающихся кубов и сферы в пространстве. Нетрудно заметить, что графика пакета приблизительно (с точностью до сегмента) вычисляет области пересечения фигур. С помощью контекстно-зависимого меню правой кнопки мыши (оно показано на рис. 8.45) можно устанавливать условия обзора фигур, учитывать перспективу при построении и т.д. В частности, фигуры на рис. 8.45 показаны в перспективе.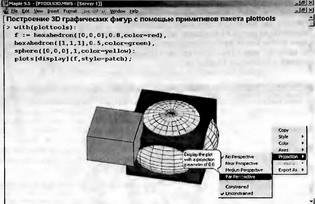

Рис. 8.45. Примеры применения примитивов трехмерной графики пакета plottools

Построение еще одной забавной трехмерной фигуры — «шкурки ежа» — демонстрирует рис. 8.46. В основе построения лежит техника создания полигонов.

Рис. 8.46. Построение трехмерной фигуры — «шкурки ежа»

Построение фигур, очень напоминающих улитки, показано на рис. 8.47. При построении этих фигур используется функция tubeplot. Обратите внимание на то, что строятся две входящие друг в друга «улитки».

Рис. 8.47. Построение фигур — «улитки»

Наконец, на рис. 8.48 показано построение фигуры — бутылки Клейна. Фигура задана рядом своих фрагментов, определенных в процедуре cleinpoints. Эта процедура является еще одним наглядным примеров программирования графических построений с помощью Maple-языка.

Рис. 8.48. Построение фигуры «бутылка Клейна»

С другими возможностями этого пакета читатель теперь справится самостоятельно или с помощью данных справочной системы. Много примеров построения сложных и красочных фигур с применением пакета plottools можно найти в Интернете на сайте фирмы Maple Software, в свободно распространяемой библиотеке пользователей системы Maple и в книгах по этой системе.

В ряде случаев бывает необходимо строить графики, представляющие собой множество однотипных фигур. Для построения таких графиков полезно использовать функцию повторения seq(f,i=a..b). На рис. 8.49 показано построение фигуры, образованной вращением прямоугольника вокруг одной из вершин.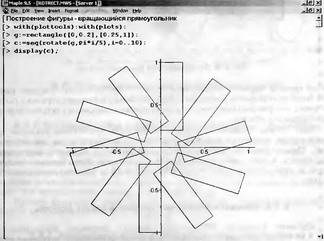

Рис. 8.49. Построение фигуры, образованной вращением прямоугольника

В этом примере полезно обратить внимание еще и на функцию поворота фигуры — rotate. Именно сочетание этих двух функции (мультиплицирования и поворота базовой фигуры — прямоугольника) позволяет получить сложную фигуру, показанную на рис. 8.49.

Пакет plottools открывает возможности реализации анимационной графики. Мы ограничимся одним примером анимации двумерных графиков. Этот пример представлен на рис. 8.50. В этом примере показана анимационная иллюстрация решения дифференциального уравнения, описывающего незатухающий колебательный процесс. Строится качающийся объект — стрелка с острием вправо, решение дифференциального уравнения в виде синусоиды и большая стрелка с острием влево, которая соединяет текущую точку графика синусоиды с острием стрелки колеблющегося объекта.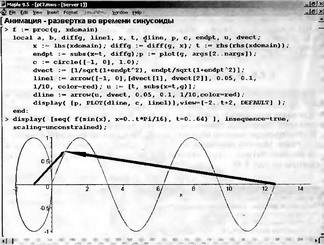

Рис. 8.50. Пример анимации двумерной графики

Этот пример наглядно показывает возможности применения анимации для визуализации достаточно сложных физических и математических закономерностей. Перспективы применения системы Maple 9.5 в создании виртуальных физических и иных лабораторий трудно переоценить. Хотя большие возможности в этой области представляет СКМ MATLAB с пакетом расширения Simulink.

Хорошим примером 3D-анимации является документ, показанный на рис. 8.51. Представленная на нем процедура springPlot имитирует поведение упругой системы, первоначально сжатой, а затем выстреливающей шар, установленный на ее верхней пластине. Упругая система состоит из неподвижного основания, на котором расположена упругая масса (например, из пористой резины), и верхней пластины.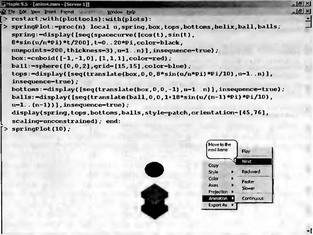

Рис. 8.51. Имитация отстрела шара сжатой упругой системой

Управление анимацией, реализованной средствами пакета plottools, подобно уже описанному ранее. Последний пример также прекрасно иллюстрирует возможности применения Maple 9.5 при математическом моделировании различных явлений, устройств и систем.

Обычно если в строке ввода задается построение нескольких графиков, то в строке вывода все они располагаются по вертикали. Это не всегда удобно, например, при снятии копий экрана с рядом графиков, поскольку экран монитора вытянут по горизонтали, а не по вертикали. Однако при применении функций plots и display можно разместить ряд двумерных графиков в строке вывода по горизонтали. Это демонстрирует пример, показанный на рис. 8.52.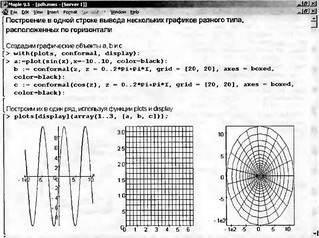

Рис. 8.52. Пример расположения трех графиков в строке вывода по горизонтали

Пример достаточно прост и нагляден, так что читатель может пользоваться данной возможностью всегда, когда ему это нужно.

В пакете plots имеется функция для конформные отображений:

conformal(F, r1, r2, о)

где F — комплексная процедура или выражение; r1, r2 — области, задаваемые в виде а..b или name=a..b; о — управляющие параметры. Таким образом, для построения нужного графика достаточно задать нужное выражение и области изменения r1 и r2. Пример построения конформных изображений для трех выражений дан на рис. 8.53.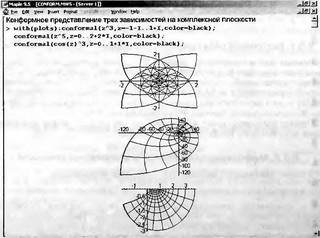

Рис. 8.53. Конформное отображение на комплексной плоскости графиков трех зависимостей

Средства конформного отображения в Maple 9.5/10, к сожалению, остаются рудиментарными и вряд ли достаточными для специалистов в этой области математики.

Некоторые виды математической графики имеют определенную художественную ценность и фигурируют в символике различных стран и общественных организаций. Остановимся на нескольких таких примерах применительно к графике в полярной системе координат. Представим фигуры, образованные множеством линий на плоскости.

Рис. 8.54 демонстрирует две из таких фигур. Первая это семейство из 10 кардиоид разного размера, построенных функцией polarplot. Параметр scalling=constrained обеспечивает правильное отображение фигур — каждая кардиоида вписывается в огибающую ее невидимую окружность. Размер кардиоид задается значением параметра а.

Рис. 8.54. Семейство кардиоид на одном графике и крест из пяти фигур на комплексной плоскости

Вторая фигура представляет собой пять фигур, построенных функций complexplot, дающей построение графиков функций комплексной переменной на комплексной плоскости. В данном случае фигуры образуют крест.

По образу и подобию приведенных фигур читатель может опробовать свои силы в создании новых красочных фигур в полярной системе координат. Некоторые из них поразительно напоминают снежинки, картинки в калейдоскопе и изображения морских звезд. Если убрать параметр color=black, введенный ради черно-белой печати картинок в книге, то можно усилить красочность фигур за счет их разноцветной окраски.

Импликативные функции нередко имеют графики весьма любопытного вида. Ограничимся парой примеров построения таких графиков, представленных на рис. 8.55. Эти фигуры напоминают контурные графики функции двух переменных.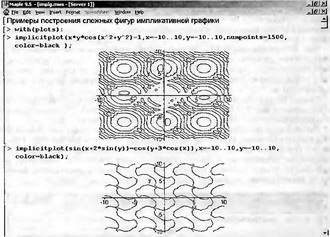

Рис. 8.55. Построение сложных фигур, изданных импликативными функциями

Приведенные примеры дают весьма наглядное представление о больших возможностях визуализации решений самых различных задач в системе Maple Можно значительно расширить их, эффектно используя описанные ранее приемы анимации изображений. В целом надо отметить, что графические возможности Maple дают новый уровень качества графики современных математических систем, о котором с десяток лет тому назад можно было только мечтать.

Maple дает прекрасные возможности для визуализации поверхностей, имеющих множество пиков и впадин, другими словами, экстремумов. Рисунок 8.56 показывает задание «вулканической» поверхности с глубокой впадиной, окруженной пятью пиками. Здесь полезно обратить внимание на способ задания такой поверхности f(a, b, с) как функции трех переменных a, b и с. Он обеспечивает индивидуальное задание координат каждого экстремума и его высоты (отрицательной для впадины).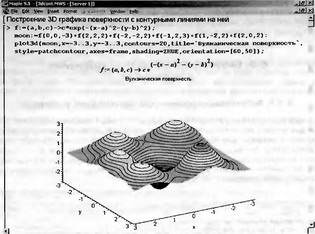

Рис. 8.56. Построение графика поверхности с множеством экстремумов

Наглядность этого графика усилена за счет применения функциональной окраски и контурных линий, нанесенных на саму поверхность. Все эти возможности обеспечивают параметры основной функции plot3d.

А на рис. 8.57 представлен еще один способ задания поверхности — с помощью функции двух угловых переменных f(θ, φ).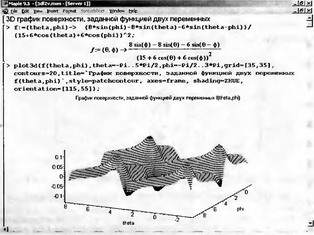

Рис. 8.57. Построение графика поверхности, заданной функцией двух угловых переменных

При построении этого рисунка также используются функциональная окраска и построение контурных линий.

Системы линейных уравнений могут решаться как с помощью функции solve, так и с помощью матричных методов. Замечательной возможностью функции solve является возможность решения относительно ограниченного числа переменных. Например, систему линейных уравнений с переменными х, у, z, t и v можно решить относительно только первых трех переменных х, у и z. При этом решения будут функциями относительно переменных t и v и можно будет построить наглядный график решения (рис. 8.58).

Рис. 8.58. График, представляющий решения системы линейных уравнений

На рис. 8.58 система задана пятью равенствами: e1, e2, e3, е4 и е5. Затем функцией solve получено вначале решение для всех переменных (для иллюстрации), а затем для трёх переменных х, у и z. Для получения решения в виде списка, а не множества, как в первом случае для всех переменных, использована функция подстановки subs. После этого функция plot3d строит плоскость решения в пространстве.

Пожалуй, еще более полезным и наглядным средством является визуализация решения системы уравнений в виде неравенств. В пакете plots имеется специальная графическая функция inequal, которая строит все граничные линии неравенств и позволяет раскрасить разделенные ими области различными цветами:

inequal(ineqs, xspec, yspec, options)

Параметры этой функции следующие: ineqs — одно или несколько неравенств или равенств или список неравенств или равенств; xspec — xvar=min_x..max_x; yspec — yvar=min_y..max_y; о — необязательные параметры, например, указывающие цвета линий, представляющих неравенства или равенства, и областей, образованных этими линиями и границами графика. Пример применения этой функции представлен на рис. 8.59.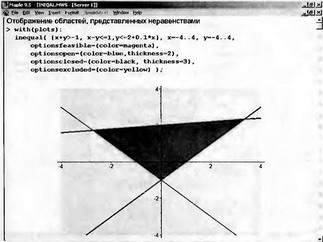

Рис. 8.59. Пример графической интерпретации решения системы неравенств

Обратите внимание на задание цветов: optionsfeasible задает цвет внутренней области, для которой удовлетворяются все неравенства (равенства), optionsopen и optionsclosed задают цвета открытых и закрытых границ областей графика, optionsexcluded используется для цвета внешних областей. График дает весьма наглядную интерпретацию действия ряда неравенств (или равенств).

Классическим методом решения нелинейных уравнений является сведение их к виду х = f(x) и применение метода простых итераций х_k = s(х_k-1) при заданном значении x₀. Приведем пример такого решения:

> f := х ->3*ln(x+1);

> x||0 := 0.5;

> x0 := .5;

> for k from 1 to 16 do x||k := evalf(f(x||(k-1))); od;

Нетрудно заметить, что значения х_k в ходе итераций явно сходятся к некоторому значению. Проведем проверку решения, используя встроенную функцию solve:

> f(x) = х; solve(%, х);

Результат выглядит необычно — помимо довольно очевидного корня х=0 значение другого корня получено в виде специальной функции Ламберта. Впрочем, нетрудно найти и его численное значение:

> evalf(%);

К нему и стремятся промежуточные результаты решения. Однако как сделать процесс решения достаточно наглядным? Обычно для этого строят графики двух зависимостей — прямой х и кривой f(x) — и наносят на них ступенчатую линии перемещения точки х_k. Специальной функции для графиков подобного рода Maple не имеет. Однако можно составить специальную процедуру для их построения. Ее листинг, взятый из примера, описанного в пакете обучения системе Maple — PowerTools —представлен на рис. 8.60.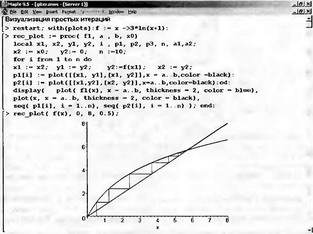

Рис. 8.60. Иллюстрация процесса итераций

На рис. 8.60 представлено задание процедуры rec_plot( f1, а, b, х0).

Параметрами этой процедуры являются: f1 — функция f(x): а и b — пределы изменения х при построении графика; х0 — значение х, с которого начинаются итерации. Используя эту процедуру можно наблюдать график, иллюстрирующий итерационный процесс. Он представлен на рис. 8.60 снизу.

Нетрудно заметить, что для данной функции процесс итераций, хотя и не очень быстро, но уверенно сходится к точке пересечения прямой у=х и кривой y=f(x). Вы можете, меняя зависимость f(x), провести исследования сходимости уравнений x=f(x).

Теперь займемся довольно рискованным экспериментом — наблюдением ньютоновских итераций с их представлением на комплексной плоскости. На рис. 8.61 задана функция f(z) комплексного аргумента. Проследить за поведением этой функции на комплексной плоскости в ходе ньютоновских итераций в соответствии с выражением z=f(z) позволяет графическая функция complexplot3d из пакета plots.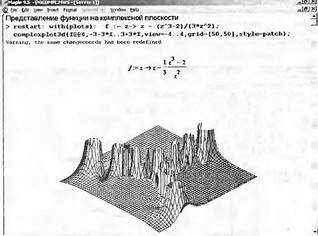

Рис. 8.61. Наблюдение за процессом ньютоновских итераций в трехмерном пространстве

Наблюдаемая картина весьма необычна и свидетельствует о далеко не простом ходе итерационного процесса. А рискованной эта задача названа потому, что в предшествующих версиях Maple она нередко вела к «зависанию» компьютера.

Средства Maple 9.5 весьма удобны для визуализации геометрических построений.

Примером наглядного геометрического представления математических понятий является визуализация известной теоремы Пифагора (рис. 8.62).

В этом примере используется функция построения многоугольников. Наглядность построений усиливается выбором разной цветовой окраски треугольников и квадрата.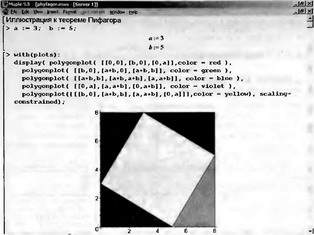

Рис. 8.62. Графическая иллюстрация к теореме Пифагора

В ряде геометрических построений нужно строить касательную и перпендикуляр к кривой, отображающей произвольную функцию f(x) в заданной точке х=а. Рисунок 8.63 поясняет, как это можно сделать. Линии касательной Т(х) и перпендикуляра N(x) определены аналитически через производную в заданной точке.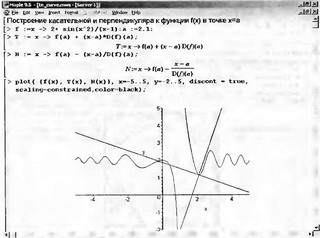

Рис. 8.63. Построение касательной и перпендикуляра к заданной точке графика функции f(x)

Во избежание геометрических искажений положения касательной и перпендикуляра при построении графика функцией plot надо использовать параметр scaling=constrained.

Часто возникает необходимость в геометрическом представлении определенных интегралов в виде алгебраической суммы площадей, ограниченных кривой подынтегральной функции f(x), осью абсцисс х и вертикалями х=a и х=b (пределами интегрирования). При этом желательно обеспечение закраски верхней и нижней (отрицательной и положительной) площадей разными цветами, например, зеленым для верхней площади и красным для нижней. Как известно, численное значение определенного интеграла есть разность этих площадей.

К сожалению, в Maple 8 нет встроенной функции, явно дающей такое построение. Однако ее несложно создать. На рис. 8.64 представлена процедура a_plot, решающая эту задачу. Параметрами процедуры являются интегрируемая функция f(x) (заданная как функция пользователя), пределы интегрирования а и b и пределы слева am и справа bm, задающие область построения графика f(x).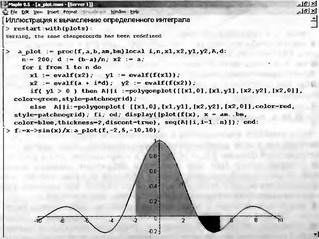

Рис. 8.64. Графическое представление определенного интеграла

Рисунок 8.64 дает прекрасное представление о сущности интегрирования для определенного интеграла. Приведенную на этом рисунке процедуру можно использовать для подготовки эффектных уроков по интегрированию разных функций.

Анимация позволяет повысить наглядность некоторых математических операций. Обычно для этого используются функции animate и animate3d пакета расширения plots, загружаемые командой with(plots). Пример этого представлен на рис. 8.65. Этот документ внизу показывает кадр анимированного процесса улучшения приближения синусоидальной функции рядом с различным числом членов (и порядком последнего члена ряда).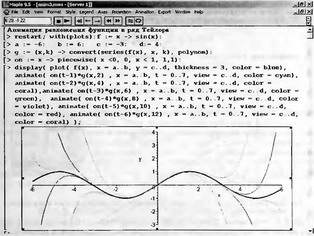

Рис. 8.65. Анимационная демонстрация приближения синусоиды рядом с меняющимся числом членов

Результирующая картина, показанная на рис. 8.65, показывает как приближаемую синусоидальную функцию, так и графики всех рядов, которые последовательно выводятся в ходе анимации.

Анимирование изображений является одним из самых мощных средств визуализации результатов моделирования тех или иных зависимостей или явлений. Порою изменение во времени одного из параметров зависимости дает наглядное представление о его математической или физической сути.

Здесь мы расширим представление об анимации и рассмотрим не вполне обычный пример — наблюдение в динамике за гармоническим синтезом некоторой произвольной функции f(x) на отрезке изменения x от 0 до 1. Значения функции f(x) могут быть одного знака или разных знаков. В этом примере можно наблюдать в динамике синтез заданной функции рядом Фурье с ограниченным числом синусных членов (гармоник) — до 1, 2, 3...N. На рис. 8.66 представлен документ, реализующий такое разложение и затем синтез для пилообразного линейно нарастающего импульса, описываемого выражением f(x)=-1+2*x. На графике строится исходная функция и результат ее синтеза в динамике анимации.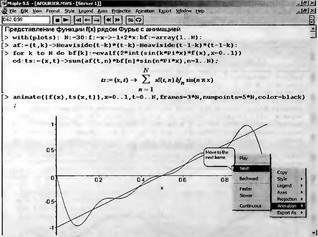

Рис. 8.66. Один из первых стоп-кадров анимации разложения импульса в ряд Фурье

Рис. 8.67 показывает завершающий стоп-кадр анимации, когда число гармоник N равно 30. Нетрудно заметить, что такое число гармоник в целом неплохо описывает большую часть импульса, хотя в его начале и в конце все еще заметны сильные отклонения.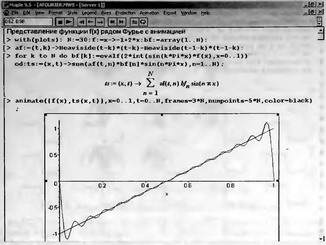

Рис. 8.67. Второй (завершающий) кадр анимации

Для f(x) = 1 строится приближение для однополярного импульса с длительностью 1 и амплитудой 1, при f(x)=x приближение для пилообразного линейно нарастающего импульса, при f(x)=x^2 — приближение для нарастающего по параболе импульса, при f(x) = signum(x-1/2) — приближение для симметричного прямоугольного импульса — меандра и т.д. Фактически можно наблюдать анимационную картину изменения формы импульса по мере увеличения числа используемых для синтеза гармоник. Выбор используемого числа гармоник осуществляет амплитудный селектор — функция af(t, k), основанная на применении функции Хевисайда.

Самым интересным в этом примере оказывается наблюдение за зарождением и эволюцией эффекта Гиббса — так называют волнообразные колебания на вершине импульса, связанные с ограничением числа гармоник при синтезе сигнала. С ростом числа гармоник эффект Гиббса не исчезает, просто обусловленные им выбросы вблизи разрывов импульса становятся более кратковременными. Амплитуда импульсов может достигать 9% от амплитуды перепадов сигнала, что сильно ухудшает приближение импульсных сигналов рядами Фурье и вынуждает математиков разрабатывать особые меры по уменьшению эффекта Гиббса.

Можно ли наблюдать одновременно все фазы анимации? Можно! Для этого достаточно оформить анимационную картину, созданную функцией animate, в виде отдельного графического объекта, например, g, после чего можно вывести все его фазы оператором display. Это и иллюстрирует рис. 8.68. На этот раз задано f(x)=signum(x-1/2) и N=25. Таким образом, рассматриваются симметричные прямоугольные импульсы — меандр. У каждого рисунка координатные оси с делениями удалены параметром axes=none.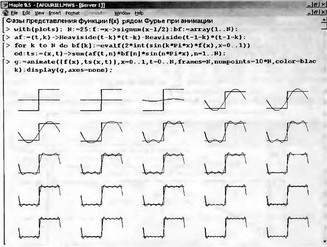

Рис. 8.68. Иллюстрация получения всех кадров анимации двумерного графика

Любопытно отметить, что при определенных числах гармоник связанная с колебательными процессами неравномерность вершины импульса резко уменьшается. Наблюдение этого явления и является наиболее интересным и поучительным при просмотре данного примера.

При внимательном просмотре рис. 8.68 заметно, что, после некоторого периода установления, фазы анимационной картинки практически повторяются. Это связано с известным обстоятельством — установившийся спектр меандра содержит только нечетные гармоники. Поэтому, к примеру, вид спектрального разложения при 22 гармониках будет тот же, что и при 21 гармонике, при 24 гармониках тот же, что при 23 и т.д. Однако, эта закономерность проявляется только при установившемся (стационарном) спектре.

Наблюдение за развитием поверхности производит на многих (особенно на студентов) большое впечатление. Оно позволяет понять детали создания сложных трехмерных графиков и наглядно представить их математическую сущность.

Как и для случая анимации двумерного графика, большой интерес представляет построение всех фаз анимации на одном рисунке. Делается это точно так же, как в двумерном случае. Это иллюстрирует рис. 8.69. На нем представлены 8 фаз анимации трехмерной поверхности cos(f*x*y/3), представленной функцией трех переменных t, х и у. При этом изменение первой переменной создает фазы анимации поверхности.

Рис. 8.69. Фазы анимации трехмерной поверхности

Применение анимации дает повышенную степень визуализации решении ряда задач, связанных с построением двумерных и трехмерных графиков. Следует отметить, что построение анимированных графиков требует дополнительных и достаточно существенных затрат оперативной памяти. Поэтому злоупотреблять числом стоп-кадров таких графиков не стоит.

Наряду с описанной выше формой применения функций анимации animate и animate3d возможны и иные формы их применения. Ограничимся парой примеров такого применения. В приведенном ниже примере анимация импликативного графика заключается в превращении окружности в наклонный эллипс:

> with(plots) :

plots[animate](implicitplot, [х^2+А*х*y+y^2=2, x=-2..2, y=-2..2,

 grid=[50,50]], A=0..1, frames=25);

Для этого задано 25 кадров (фреймов) изменения параметра А от 0 до 1. В другом примере анимация задает деформацию мембраны в виде квадрата с жестко закрепленными границами:

> plots[animate](plot3d, [sin(А)*ехр(-х^2-y^2), х=-2..2, y=-2..2],

 А=0..2*Pi);

Ввиду очевидности этих примеров графики результатов их выполнения не приводятся — пользователь может просмотреть их самостоятельно.

Иногда возникает необходимость сменить координаты к какого-то графика или изменить масштаб по определенной оси. Первая задача может несколько озадачить пользователя. Однако она легко решается средствами графики пакета stats — см. примеры на рис. 8.70. Масштабирование и сдвиг решаются проще — введением масштабных коэффициентов и констант сдвига. Но и эти задачи еще проще решаются указанными выше средствами графики.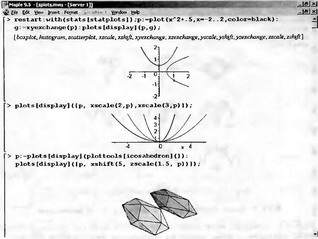

Рис. 8.70. Примеры смены координат и масштабирования графиков

В первом примере рис. 8.70 используется функция xyexchange(p) меняющая оси у графического объекта р. Во втором случае используется функция xscale(k,p) масштабирующая объект по оси х в k раз. А в третьем примере используется функция сдвига объекта xshift(xs,p) на расстояние xs и масштабирования zscale(k,p) в k раз по оси z. О других функциях подпакета статистической графики можно судить по названиям его функций.

В пакет plots была введена новая функция построения стрелок в пространстве arrow. Она задается в виде:

arrow(u,[v,]opts)

или

arrow(U,opts)

Построение стрелок задается по одномерными массивами координат начала стрелок и их направления u и v или двумерным массивом U, которые могут быть представлены векторами, списками или множествами. Вид стрелок задается параметром opts, который может иметь значения shape, length, width, head_width, head_length или plane и задает вид стрелок (форму, длину, ширину и т.д.). Детали задания параметров можно найти в справке по данной функции. Рис. 8.71 дает наглядное представление о ее возможностях.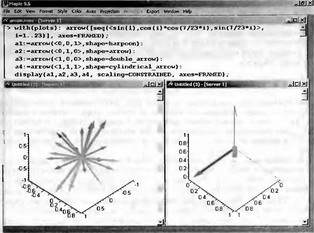

Рис. 8.71. Построение стрелок с помощью функции arrow

Maple 9.5 позволяет строить достаточно сложные комбинированные графики, содержащие различные графические и текстовые объекты. Пример построения такого графика представлен на рис. 8.72.

Рис. 8.72. Пример построения сложного объекта, состоящего из 8 графических и текстовых объектов

Представленный на рис. 8.72 объект задает построение восьми графических объектов от р1 до р8. Среди них цилиндр, две пересекающие его плоскости и иные (в том числе текстовые) объекты. Обратите внимание на способ вывода этих объектов функцией display3d. Этот пример показывает, что с помощью графических программных средств Maple 9 можно строить достаточно замысловатые графики, которые могут использоваться для визуализации тех или иных геометрических и иных объектов.

Дифференциальные параметры функции f(x), описывающей некоторую кривую, имеют большое значение для анализа ее особых точек и областей существования. Так, точки с нулевой первой производной задают области, где кривая нарастает (первая производная положительна) или убывает (первая производная отрицательна) с ростом аргумента х. Нули второй производной задают точки перегиба кривой.

Для такого анализа особенно удобен новый пакет Calculus 1, включенный в пакет расширения Student. На рис. 8.73. показано применение функции FunctionChart для визуализации дифференциальных параметров кривой, которая представляет собой сложную функцию. По умолчанию анализ ведется в интервале изменения х от -10 до +10. Экстремальные точки помечаются ромбиком, точки перегиба крестиком, нули кружочками, а области кривых — заливкой цветом.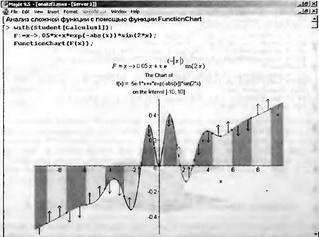

Рис. 8.73. Анализ и визуализация сложной функции, заданной функцией пользователя

Рисунок 8.73 дает наглядное представление о поведении заданной функции. Рекомендуется опробовать данную процедуру на других функциях. Следует отметить, что, поскольку процедура использует функции minimize и maximize, она может давать сбои при исследовании сложных функций, содержащих специальные математические функции или особенности. Данная процедура дает хорошие результаты при анализе функций, представленных полиномами.

Функция FunctionChart может использоваться с многочисленными опциями, существенно влияющими на вид рисунка — рис. 8.74. В данном случае анализируется функция sin(x)/x.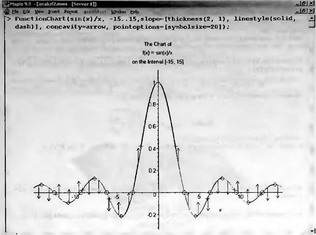

Рис. 8.74. Визуализация функции sin(x)/x

Визуализация функций весьма полезна в учебных целях при детальном изучении свойств той или иной функции.

В ряде случаев обычная техника анимации оказывается не очень подходящей из-за ограничений на выбор опций. Такова, например, ситуация, когда желательно обеспечить анимацию с большим числом кадров сложной поверхности, освещаемой от некоторого источника света. Пример такого рода представлен на рис. 8.75.

Рис. 8.75. Задание поверхности — мембраны

На рис. 8.76 задана упругая поверхность мембраны, закрепленной по периметру. Мембрана имеет ряд выпуклостей и впадин, переходящих друг в друга. Начальный вид мембраны представлен на рис. 8.76. Там же показано контекстное меню мыши, с помощью которой можно запустить анимацию — в том числе по кадрам.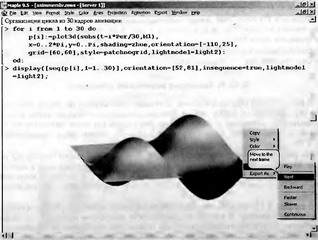

Рис. 8.76. Организация анимации мембраны и ее начальное положение

А на рис. 8.77 представлен промежуточный кадр анимации, из которого хорошо виден ее характер. В частности, выпуклости мембраны переходят во впадины и наоборот. С учетом выбранной схемы освещения мембраны ее колебания выглядят очень эффектно и наглядно, что особенно ценно при использовании подобных примеров в образовании.

Рис. 8.77. Промежуточный кадр анимации поверхности мембраны

Различные поля (электрические, гидравлические, гравитационные и иные) относятся к достаточно сложным понятиям, визуализация которых представляет значительные трудности в связи с большим объемом вычислений параметров поля, выполняемых во многих точках пространства с разными системами координат и отсутствием у людей органов для наблюдения полей.

В пакете VectorCalculus можно найти функции, которые совместно с графикой ряда других пакетов обеспечивают высокую степень визуализации полей с помощью стрелок, направления и размеры которых указывают на количественные оценки полей и изменения их градиентов в различных точках полей. Не вдаваясь в тонкости математической и физической интерпретации таких графических построений, приведем несколько примеров их выполнения, иллюстрирующих возможности рассматриваемого пакета в визуализации полей.

Рисунок 8.78 иллюстрирует поиск трех локальных экстремумом поверхности, представленной функцией двух переменных. Экстремумы — минимумы ищутся с помощью функции fsolve по нулям частных производных по поверхности, вычисляемым функцией cliff пакета VectorCalculus. Это расширяет методы поиска экстремумов функций двух переменных.

Рис. 8.78. Визуализация поиска локальных минимумов поверхности

В найденных точках минимумов размещены черные сферы, что позволяет наглядно представить положение точек минимума поверхности. Правда, сферы выглядят как эллипсоиды, поскольку при выводе графиков выравнивание масштабов изображения по всем трем осям не предусматривалось.

На рис. 8.79 представлена визуализация стрелками поля функции F и вихря F_curl. Заинтересованному читателю нетрудно разобраться с тем, какие стрелки представляют эти графические объекты — к сожалению для их представления в виде черно-белого рисунка книги пришлось отказаться от цветового выделения стрелок, которое существенно повышает наглядность подобных графиков.

Рис. 8.79. Пример визуализации векторного поля функции и ее вихря

На другом рисунке (рис. 8.80) стрелками представлена трехмерная поверхность F, а сплошными линиями дивергенция ее поля, предварительно вычисленная в приведенном фрагменте документа.

Рис. 8.80. Пример визуализации поверхности стрелками и дивергенции ее поля

Эта техника визуализации может быть распространена и на другие характеристики поверхностей и полей.

С интегральными представлениями в теории поля связан ряд фундаментальных теорем Грина, Стокса, Остроградского и др. Средства пакета VectorCalculus открывают обширные возможности по наглядному представлению этих и иных положений теории поля. В качестве примера на рис. 8.81 представлена визуализация положений теоремы Стокса.

Рис. 8.81. Иллюстрация теоремы Стокса

Рассмотрим поле двух точечных единичных зарядов, расположенных на расстоянии 0,25 м друг от друга. Нас интересует визуализация картины электрического поля между ними для случая, когда заряды равны по величине и противоположны по знаку. Воспользуемся упрошенной формулой для вычисления потенциала любой точки (х, у) из которой удален множитель 1/4πε. Рисунок 8.82 показывает применение этой формулы для построения трехмерного графика распределения потенциала для двух зарядов (положительного и отрицательного), расположенных на расстоянии 0,25 (единицы условные).

Рис. 8.82. Расчет и построение графика нормированного распределения поля двух зарядов противоположных знаков

Потенциал зарядов pot(x,y) представляет поверхность с пиком для положительного заряда в точке (0, 0) и впадиной в точке (0,25,0). Ввиду упрощения выражения для заряда точных данных эта зависимость не несет и используется для качественных представлений.

Так, в электротехнике, однако, чаще используют графики поля в виде контурных эквипотенциальных линий. Построение такого графика для поля и его градиента (графика напряженности поля) показано на рис. 8.83. К сожалению, функциональная окраска графика поля отчетливо видна лишь на экране цветного дисплея. Оцифровка линий контурного графика, к сожалению, не предусмотрена.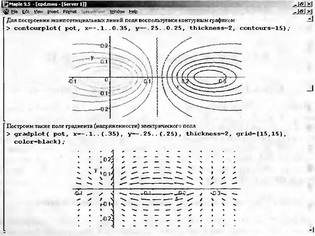

Рис. 8.83. Контурные графики электрического поля и его градиента

Иногда полезно отслеживать изменение графика электрического поля при изменении одного из зарядов. Рис. 8.84 показывает пример построения такого анимационного графика при изменении величины правого заряда с отрицательного на положительный. Представлен один из кадров анимации.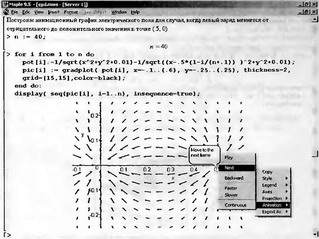

Рис. 8.84. Пример построения анимационного графика поля двух зарядов при изменении правого заряда

Большое число других примеров на вычисление параметров полей и визуализацию их можно найти в размещенных в Интернете (на сайте корпорации Waterloo Maple) пакетах Calculus IV и V.

Возможности двумерной графики в системах Maple 9.5 и 10 практически равноценны. В Maple 10 расширены возможности форматирования двумерных графиков с помощью средств позиции Plot меню и контекстного меню правой клавиши мыши. Введена новая опция gridlines для функции plot, позволяющая выводить (в том числе раздельно по осям) линии масштабной сетки. Пример ее применения был представлен на рис. 1.49. Эта опция и новые формы синтаксиса функции plot доступны только при стандартном интерфейсе Maple 10 — при классическом интерфейсе они просто не работают.

Незначительному улучшению подверглись средства трехмерной графики. Введена новая опция glossiness (лоск, глянец) улучающая вид графика при окраске поверхности. Ее влияние иллюстрирует рис. 8.85 (сверху).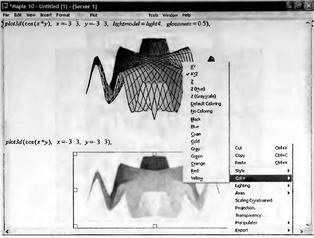

Рис. 8.85. Трехмерная графика в Maple 10

Здесь также особенно важно отметить возможность форматирования уже построенных графиков с помощью средств позиции Plot меню и контекстного меню правой клавиши мыши. Последнее показано на рис. 8.85 для нижнего рисунка, в котором показан пример применения функции plot3d в обычном виде (без новой опции).

В Maple 10 введены новые графические объекты — наброски (sketch — набросок). Они напоминают бумагу, разлинованную в клетку, на которой можно рисовать электронным карандашом (pencil) или распылителем (Highlighter). Есть также стиралка Eraser. Вставка наброска (см. рис. 8.86) выполняется командой sketch в позиции меню Insert. Средства работы с набросками сосредоточены в специальной позиции меню Sketch, представленной на рис. 8.86 в открытом виде.

Рис. 8.86. Пример вставки наброска и рисования в нем

Те же самые средства имеются в контекстном меню правой клавиши мыши. Для редактирования набросков служит команда Canvas Style..., которая выводит окно редактирования, представленное на рис. 8.87. В окне можно задавать вывод вертикальным и горизонтальных линий сетки, устанавливать расстояние между ними (шаг) и изменять цвета объектов наброска — линий разметки и фона. Окно выбора цвета показано также на рис. 8.87.

Рис. 8.87. Окно редактирования набросков (слева) и окно установки цвета (справа)

Команда Stroke Styles… открывает окно установки стиля карандаша и распылителя, показанное на рис. 8.88 с открытой вкладкой карандаша. Помимо заведомо определенных стилей можно задать свой собственный стиль и установить для него толщину линии и ее цвет. Аналогичные средства для распылителя есть на второй вкладке этого окна.

Рис. 8.88. Окно установки стилей карандаша и распылителя

Представленные выше графики записаны в файл newg_m10. Применение графических набросков разнообразит документы системы Maple 10