Мы уже рассмотрели множество математических и научно-технических задач самого общего характера. Некоторые из них могут показаться на первый взгляд абстрактными. Поэтому в этой главе приводится полное решение целого ряда вполне конкретных учебных и научно-технических задач из области физики, квантовой механики, электро-радиотехники и акустики [22, 23, 53, 54]. Эти задачи хорошо иллюстрируют технику решения научно-технических задач в среде системы Maple путем математического моделирования. Рекомендуется также просмотреть примеры применения системы Maple 10.

Резонансные LCR-контуры в электрорадиотехнике, механические маятники и даже молекулы и атомы различных веществ — все это примеры систем второго порядка. Они могут быть линейными и нелинейными, сильно или слабо демпфированными и находящимися в режиме свободных колебаний или под внешним воздействием.

Замечательно то, что огромное число таких систем описывается системой из двух линейных дифференциальных уравнений или одним линейным дифференциальным уравнением второго порядка. Рассмотрим типичную сильно демпфированную систему — вне зависимо от ее конкретной реализации. Проведем ее анализ и выполним моделирование, ограничившись поначалу минимумом средств системы Maple.

Рис. 11.1. Задание дифференциального уравнения второго порядка для сильно демпфированной системы второго порядка

Рис. 11.1 представляет начало документа, в котором задано нормированное дифференциальное уравнение второго порядка, записанное в виде, известном из учебников по теории колебаний, радио- или электротехники. Здесь же построен характеристический полином данного дифференциального уравнения и найдены его корни. Они оказались действительными, что является признаком апериодичности анализируемой системы. И отрицательными, что указывает на затухание собственных колебаний системы.

Дифференциальное уравнение DE представленного вида имеет два параметра — параметр p определяющий степень демпфирования системы и параметр q, определяющий резонансную частоту системы. В данном примере в качестве внешнего воздействия используется синусоидальное воздействие (сигнал в радиотехнических системах). Для решения дифференциального уравнения надо задать его начальные условия. Все это и сделано на рис. 11.1.

Поскольку Maple — система символьной математики, то она позволяет получить результат моделирования системы второго порядка в аналитическом виде. Это и показано на рис. 11.2. Здесь даны два решения — одно при отсутствии воздействия и другое при наличии воздействия. Нетрудно заметить, что решения представлены в аналитическом виде и достаточно просты, хотя и не имеют привычного нормированного вида. Обратите внимание на то, что решение при отсутствии воздействия представлено только экспоненциальными членами с отрицательными показателями степени. Это говорит об апериодическом поведении системы и затухании в ней энергии.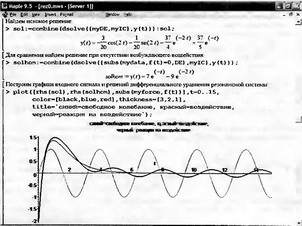

Рис. 11.2. Решение задачи моделирования системы второго порядка при синусоидальном воздействии

График исходного воздействия и реакций системы также представлен на рис. 11.2. Нетрудно заметить, что при р=3 система ведет себя как типичная апериодическая система — возникшее отклонение уменьшается без колебаний. Однако при наличии воздействия его колебательная компонента появляется в реакции системы — это видно и из аналитического решения для y(t) и из графика решения.

Теперь слегка модернизируем представленный выше документ и зададим параметры p и q, соответствующие слабо демпфированной колебательной системе — рис. 11.3. Нетрудно заметить, что теперь характеристический полином имеет комплексные корни, что (для знающих теорию колебаний) указывает на колебательный характер поведения системы. Такие системы являются резонансными.

Рис. 11.3. Начало документа с примером моделирования резонансной системы с малым демпфированием при синусоидальном воздействии

Решение составленной системы представлено на рис. 11.4. Хотя мы рассматриваем достаточно простую систему, ее решение выглядит уже не слишком простым, хотя назвать его сложным было бы неверно. Решение, как при отсутствии внешнего воздействия, так и при его наличии, имеет члены с синусами и косинусами, что явно указывает на наличие периодических компонент решения.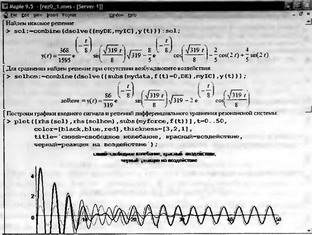

Рис. 11.4. Конец документа с примером моделирования резонансной системы с малым демпфированием при синусоидальном воздействии

Но, пожалуй, в данном случае наиболее нагляден график решений. При отсутствии воздействия он представляет собой экспоненциально затухающее колебание. А вот при наличии воздействия поведение системы гораздо сложнее. Хорошо видно более резкое уменьшение амплитуды затухающих колебаний во время первых пяти периодов. Но затем колебания начинают нарастать и, в конце концов, они вырождаются в синусоидальное колебание с частотой воздействия, но с некоторым отставанием по фазе. Налицо признаки быстро затухающих биений с разностной частотой.

Можно ли получить аналитические решения данной задачи, если воздействие имеет более сложную форму, например, широко распространенных треугольных, пилообразных или прямоугольных импульсов? Ответ на этот вопрос таков — можно, если само воздействие описывается аналитически с применением элементарных или специальных функций.

Наглядным примером может служить анализ поведения системы при воздействии на нее треугольных колебаний. Как было уже показано, такие колебания легко получить, задав их функций arcsin(sin(x)). Это и показано на рис. 11.5.

Рис. 11.5. Начало документа с примером моделирования резонансной системы с малым демпфированием при треугольном воздействии

Конец документа рис. 11.5 представлен на рис. 11.6. Здесь, прежде всего, стоит обратить внимание на аналитическое решение задачи. Увы, но в Maple 9.5 назвать его простым язык уже не поворачивается, хотя решение занимает на экране всего две строки (нередки случаи, когда решение имеет десятки-сотни строк). Любопытно, что в решение входит даже определенный интеграл. А это указывает уже на то, что время вычислений может значительно возрасти из-за вычисления интеграла численными методами.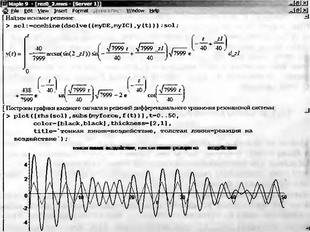

Рис. 11.6. Конец документа с примером моделирования резонансной системы с малым демпфированием при треугольном воздействии

Решение системы при отсутствии внешнего воздействия здесь не приводится, поскольку оно абсолютно идентично представленному на рис. 11.4. А вот график общего решения весьма показателен. Так, видно, что благодаря резонансу форма выходных колебаний остается синусоидальной. Но, гораздо сильнее, чем на рис. 11.4, видны биения с разностной частотой. Впрочем, что уже заметно и на рис. 11.6, они затухают, так что в стационарном режиме сигнал на выходе представляет собой синусоидальную функцию с частотой внешнего воздействия.

При произвольном воздействии ожидать возможности аналитического решения, скорее всего, уже не приходится. В качестве примера рассмотрим решение задачи на поведение резонансной системы при воздействии на нее прямоугольных импульсов. Чтобы упростить записи выражений будем считать импульсы нормированными, т. е. пусть их амплитуда будет равна π, длительность тоже равна π и период 2π. Такие импульсы можно задать, используя соотношение signum(sin(x)) и выполнив указанное выше нормирование. Это и показано на рис. 11.7.

Рис. 11.7. Представление входного сигнала рядом Фурье

К сожалению сформированный таким образом сигнал нельзя считать строго аналитическим, поскольку функция signum не относится ни к элементарным ни к специальным математическим функциям. А потому, желающие могут это легко проверить, такой сигнал не может стоять в правой части дифференциального уравнения, поскольку оно в этом случае аналитически не решается и просто повторяется в строке вывода.

Однако, подобный сигнал, как и множество других сигналов, может быть представлен своим разложением в ряд Фурье или просто синтезирован рядом гармоник, что и показано на рис. 11.7. В нем задано построение сигнала с числом гармоник N=3 и NN=10 и заданы коэффициенты a_k и b_k ряда Фурье. Заметим, что поставив после оператора od точку с запятой вместо двоеточия можно вывести значения этих коэффициентов.

Рисунок 11.8 показывает Фурье-синтез приближенного входного сигнала для 3 и 10 гармоник, а также построение сигнала вместе с идеальным (исходным) сигналом. Нетрудно заметить, что из-за эффекта Гиббса полученный сигнал (особенно при грех гармониках) довольно сильно отличается от идеального. Однако стоит не забывать, что резонансная система эффективно гасит все колебания, за исключением того, которое имеет частоту, близкую к резонансной частоте.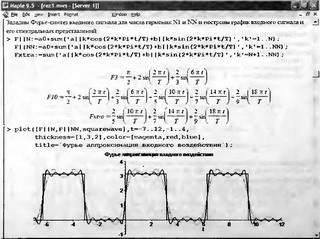

Рис. 11.8. Синтез приближенного сигнала и его сравнение с идеальным сигналом

Хотя временные зависимости сигнала, показанные на рис. 11.8 могут показаться сложными, на самом деле это всего лишь суммы синусоидальных колебаний кратной частоты. К тому же представлены только нечетные гармоники. Но главное — этот сигнал уже имеет аналитическое представление и его можно использовать в правой части дифференциального уравнения. Это и показано на рис. 11.9, где заданы дифференциальные уравнения для рассмотренных выше случаев.

Рис. 11.9. Составление дифференциального уравнения второго порядка и задание начальных условий

Теперь остается решить представленные дифференциальные уравнения получить графики полученных решений, представленные на рис. 11.10. В данном случае частоты сигнала и собственных колебании системы заметно различаются и выходной сигнал системы представляет собой, в основном, выделенную вторую гармонику воздействия.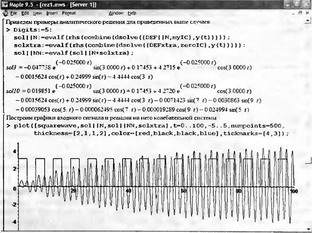

Рис. 11.10. Решение дифференциальных уравнений и его визуализация

Разумеется, представленный вариант анализа носит частный характер, поскольку синтезируется вполне конкретный вид сигнала — прямоугольные импульсы с заданными выше параметрами. Однако, если использовать разложение в ряд Фурье произвольного воздействия, то подобным способом можно решить задачу получения реакции колебательной (а, в принципе, любой линейной) системы на заданное воздействие.

Вернемся к задаче моделирования системы второго порядка и попытаемся найти решения в более удобном виде, обычно приводимом в учебниках после ряда преобразований. Для этого достаточно воспользоваться пакетом расширения DEtools. Рис. 11.11 показывает начало документа с составленным дифференциальным уравнением и его решением. Нетрудно заметить, что теперь решение представлено в классическом виде, который обычно приводится в учебниках по теории колебаний.

Рис. 11.11. Решение дифференциального уравнения свободных колебаний с применением пакета DEtools

На рис. 11.12 показана вторая часть документа с решением для конкретных данных и построением графика временной зависимости свободных колебаний. Нетрудно заметить, что свободные колебания системы имеют вид затухающих синусоидальных колебаний. Вы можете проверить, что при р<0 колебания будут нарастать по экспоненциальному закону, что характерно для генераторных систем.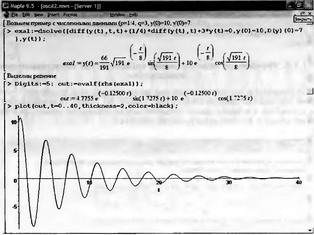

Рис. 11.12. Пример вычисления временной зависимости свободных колебаний и построения их графика

Нередко о характере колебаний удобно судить по фазовому портрету колебаний. Он задается графиком в параметрической форме, при которой по одной оси откладывается зависимость у(t), а по другой — ее производная. Это показано на рис. 11.13. Фазовый портрет в данном случае представляет собой сворачивающуюся спираль.

Рис. 11.13. Фазовый портрет затухающих свободных колебаний

По аналогии с последним примером можно рассмотреть поведение системы второго порядка при синусоидальном воздействии. На рис. 11.14 представлено начало документа, в котором задано исходное дифференциальное уравнение и получено его общее и частное аналитические решения.

Рис. 11.14. Пример аналитического решения задачи на поведение системы второго порядка при синусоидальном воздействии

На рис. 11.15 представлены временные диаграммы реакции системы и синусоидального воздействия. Кроме того, построен фазовый портрет колебаний. Он заметно отличается от спирали и хорошо иллюстрирует сложность колебаний в начале их развития.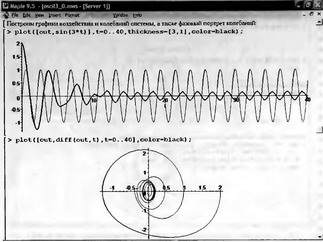

Рис. 11.15. Результаты моделирования цепи второго порядка при синусоидальном воздействии

К сожалению, применение пакета расширения DEtools усложняет функцию dsolve решения дифференциальных уравнений. В результате время моделирования даже простых систем удлиняется до минут, а более сложные системы могут потребовать куда более длительного времени моделирования. В этом случае может оказаться целесообразным отказаться от получения аналитических зависимостей для результатов моделирования и перейти к численному моделированию.

Рассмотрим методику улучшенного моделирования еще на одном примере — вычислении реакции системы при пилообразном воздействии. На рис. 11.16 показано задание такого воздействия с помощью функции floor. Для упрощения расчетных выражений амплитуда и период воздействия взяты равными я. Поскольку в данном случае аналитическое решение получить невозможно (функция floor не позволяет этого), то заменим воздействие рядом Фурье. Его коэффициенты также представлены на рис. 11.16.

Рис. 11.16. Начало моделирование системы с пилообразным воздействием, представленным рядом Фурье

На рис. 11.17 представлены графики воздействия в идеальном случае и при его представлении рядом Фурье с пятью гармоники. Показано также аналитическое решение для временной зависимости y(t) при таком воздействии.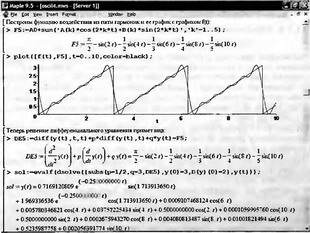

Рис. 11.17. Воздействие и временная зависимость реакции системы при пилообразной форме воздействия

Наконец на рис. 11.18 показан график реакции системы на пилообразное воздействие и фазовый портрет колебаний в ней. Нетрудно заметить, что форма воздействия достаточно слабо влияет на форму временной зависимости реакции системы на заданное воздействие. Это следствие резонансных свойств системы.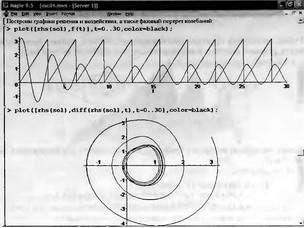

Рис. 11.18. Реакция системы на пилообразное воздействие и фазовый портрет колебании при таком воздействии

Нелинейные системы второго порядка, к сожалению, не имеют общих аналитических решений и для моделирования таких систем следует использовать численные методы решения дифференциальных уравнений. Примеры такого рода уже приводились в главе 7, посвященной решению дифференциальных уравнений. Другие примеры вы найдете ниже.

Произвольные линейные системы могут анализироваться и моделироваться хорошо известным (особенно в электротехнике и радиотехнике) операторным методом. При этом методе система и ее воздействие представляются операторными выражениями, т. е. в виде функций параметра — оператора Лапласа s (в литературе встречается и обозначение p). Не вникая в детали этого общеизвестного метода, рассмотрим конкретный пример (файл linsys). Он, для сравнения с предшествующими примерами, дан для системы второго порядка, хотя в данном случае никаких ограничений на порядок системы нет.

Для начала зададим инициализацию применяемых пакетов расширения

> restart:with(plots): readlib(spline): with(inttrans):

Warning, the name changecoords has been redefined

Далее зададим операторные выражения для коэффициента передачи системы G и входного сигнала R (в виде единичного перепада) и вычислим с упрощением их произведение:

> G := K/(M*s^2+C*s+1); R := 1/s;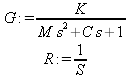

> X := simplify(R*G);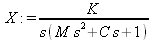

Теперь, используя обратное преобразование Лапласа, найдем временную зависимость реакции системы в аналитическом (что наиболее ценно) виде:

> h := simplify(invlaplace(X, s, t));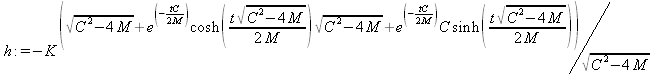

Теперь мы можем построить график этой зависимости для конкретных значений М, С и K:

> h1 : = subs(M=1,C=0.75,K=1,h);

> linresp := plot(h1, t=0..20, axes=boxed, color=black): display(linresp);

Вид этой зависимости представлен на рис. 11.19. Он соответствует реакции системы второго порядка для случая затухающих колебаний.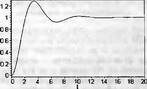

Рис. 11.19. Одна из временных зависимостей реакции системы второго порядка

А теперь зададимся целью наглядно проиллюстрировать изменение временной зависимости реакции системы при изменении параметра С от 0 до 2 при М=1 и K=1. Для этого выполним следующие вполне очевидные команды:

> х := subs(M=1, K=1, h);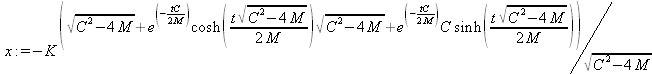

> plot3d(x, С=0..2, t=0..20, axes=boxed);

Соответствующий график показан на рис. 11.20. Он прекрасно иллюстрирует переход от апериодического режима при С=2 к колебательному при С= 0 при изменении времени от 0 до 20.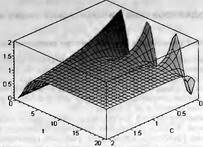

Рис. 11.20. Динамика развития колебаний в системе при изменении параметра С

Аналогичным образом можно построить трехмерный образ временной зависимости реакции системы для М=1, С=0.25 и изменении параметра K от 0 до 3. Для этого надо выполнить команды:

> x1 := subs(М=1, С=0.25, xt);

> plot3d(x1, K=0..3, t=0..20, axes=boxed);

Диаграмма временных зависимостей представлена на рис. 11.21.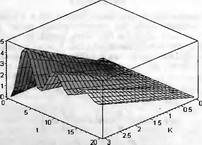

Рис. 11.21. Динамика развития колебаний в системе при изменении параметра K

Представленные на рис. 11.20 и 11.21 диаграммы дают весьма наглядное представление о динамике поведения рассмотренной системы. Но еще важнее то, что просто изменением операторной записи G и R по описанной методике можно анализировать и наглядно представлять работу множества линейных систем.

Вы хотите метнуть камень в огород вашего вредного соседа? Разумеется во время его отсутствия. Давайте промоделируем эту ситуацию, предположив два актуальных случая: дело происходит на Земле в условиях, когда наша планета лишилась воздуха и когда, слава богу, он все же есть. В первом случае сопротивления воздуха нет, а в другом сопротивление воздуха есть и его надо учитывать. Иначе камень упадет в ваш огород, а не в огород соседа!

Учет сопротивления воздуха не просто усложняет задачу нашу задачу. Он делает ее нелинейной. В связи с этим мы применим численные методы решения дифференциальных уравнений. Кроме того, учитывая громоздкость документов, описывающих приведенные ниже задачи, перейдем к их записи прямо в тексте книги.

Итак, пусть подвернувшиеся под руку камни с массой 500 и 100 грамм брошены под углом 45 к горизонту со скоростью V_O=20 м/с. Найдем их баллистические траектории, если сила сопротивления воздуха Fmp=A*V, где А=0,1 Н∙с/м. Сравним их с траекториями, получающейся без учета сопротивления воздуха. Документ с решением этой задачи, описанным ниже, представлен в файле balist.

Начнем с подключения пакета plots, нужного для визуализации данной задачи:

> restart; with(plots):

Warning, the name changecoords has been redefined

Составим параметрические уравнения для проекций скорости на оси координат:

> Vox:=Vc*cos(alpha);Voy:=Vo*sin(alpha);

Мы рассматриваем два случая: камень массой 500 г и камень массой 100 г. Поскольку для каждого случая мы предусматриваем расчет в двух вариантах (с учетом сопротивления воздуха и без такого учета), то мы должны составить 4 системы дифференциальных уравнений (ДУ). Каждая система состоит из двух ДУ второго порядка и вид этих систем известен из курса физики. Ниже представлено задание этих систем ДУ (для первой системы дан вывод ее вида):

> sys1:=massa[1]-diff(x(t), t$2) =

-A[1]*diff(x(t),t),massa[1]*diff(y(t), t$2) = -A[1]*(diff(y(t),t))-massa[1]*g;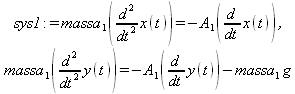

> sys2:=massa[1]*diff(x(t), t$2) =

-A[2]*diff(x(t),t),massa[1]*diff(y(t), t$2) =

-A[2]*(diff(y(t),t))-massa[1]*g;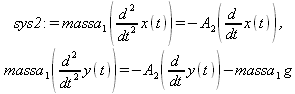

> sys3:=massa[2]*diff(x(t), t$2)=

-A[1]*diff(x(t),t),massa[2]*diff(y(t), t$2)=

-A[1]*(diff(y(t),t))-massa[2]*g;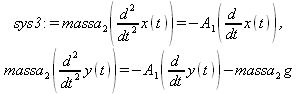

> sys4:=massa[2]*diff(x(t), t$2) =

-A[2]*diff(x(t),t),massa[2]*diff(y(t), t$2) =

-A[2]*(diff(y(t),t))-massa[2]*g;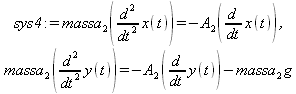

Зададим исходные числовые безразмерные данные для расчета:

> Vo:=20;massa:=[0.5,0.1];А:=[0.1,0];alpha:=Pi/4;g:=9.8;

Выполним решение заданных систем ДУ:

> pi:=dsolve({sys1,х(0)=0,D(х)(0)=Vox,y(0)=0,D(у)(0)=Voy}, {y(t),x(t)},type=numeric ,output=listprocedure):

> p2:=dsolve({sys2,x(0)=0,D(x)(0)=Vox,y(0)=C,D(y){0)=Voy}, {y(t),x(t)},type=numeric, output=listprocedure):

> p3:=dsolve({sys3,x(0)=0,D(x)(0)=Vox,y(0)=0,D(y)(0)=Voy}, {y(t),x(t)},type=numeric, output=listprocedure):

> p4:=dsolve({sys4,x(0)=0,D(x)(0)=Vox,y(0)=0,D(y)(0)=Voy}, {y(t),x(t)},type=numeric, output=listprocedure):

Создадим графические объекты - результаты решения систем ДУ:

> a1:=odeplot(p1, [x(t), y(t)], 0..3, color=green, view=[0..50,0..15], thickness=2):

> a2:=odeplot(p2, [x(t), y(t)], 0..3, color=red, view=[0..50, 0..15], thickness=2):

> a3:=odeplot(p3, [x(t), y(t)], 0..3, color=blue, view=[0..50, 0..15], thickness=2:

> a4:=odeplot(p4, [x(t), y(t)], 0..3, color=black, view=[0..50, 0..15], thickness=2):

Построим графики траекторий для первого случая:

> t:=textplot([[25,8, `А=0.1`], [35,9, `А=0`]],color=blue, font=[TIMES, ROMAN, 12])

> t1:=textplot([[17, 3, `A=0.1`], [35,9, `A=0`]], color=blue, font=[TIMES, ROMAN, 12]):

> display({a1,a2,t},title=`Траектория полета тела массой 500 г`, labels=[x,y], labelfont=[TIMES,ROMAN,14]);

Графики траекторий полета камня с массой 500 грамм представлены на рис. 11.22.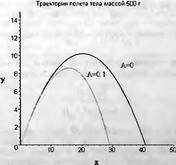

Рис. 11.22. Баллистические траектории камня с массой 500 грамм

Теперь построим графики траекторий для второго случая:

> display({a3,а4,t1},title=`Траектория полета тела массой 100 г`,

labels=[х,у], labelfont=[TIMES,ROMAN,14]);

Они представлены на рис. 11.23.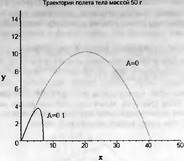

Рис. 11.23. Баллистические траектории камня при массе 100 грамм

Из проведенных расчетов и графиков видно, что при учете силы сопротивления воздуха дальность и высота полета сильно уменьшаются по сравнению с полетом в вакууме, и эта разница зависит от массы тела, поэтому при небольшой массе тела сопротивлением воздуха пренебрегать нельзя.

От реального мира перейдем к микромиру. Пусть микрочастица массой 9∙10^-31 кг и зарядом +1,6∙10^-19 Кл влетает в магнитное поле с индукцией В=0,1 Тл под углом а=80. Рассчитаем траекторию движения частицы при начальной скорости Vо=1∙10⁷ м/с (файл traekt). Начнем с рестарта:

> restart;

Сила Лоренца, действующая на движущуюся частицу F=q(E+[v, В]). Проекции векторного произведения [v, В] на оси х, у, z:

[v, B]x = vy*Bz-vz*By [v, B]y = vz*Bx-vx*Bz [v, B]z = vx*By-vy*Bz

В соответствии с этим известные из курса физики дифференциальные уравнения, описывающие траекторию полета частицы по осям х, у, z имеют вид:

> sys:=diff(х(t),t$2)=q*(Ex+(diff(у(t), t)*Bz-

diff(z(t),t)*By))/massa,diff(y(t),t$2)=q*(Ey+(diff(z(t),t)*Bx -

diff(x(t),t)*Bz))/massa,diff(z(t),t$2)=q*(Ez+(diff(x(t),t)*

By-diff(y(t),t)*Bx))/massa;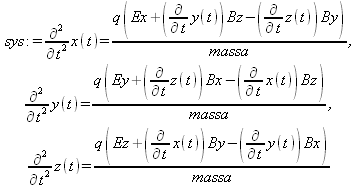

Зададим исходные числовые данные (опустив размерности):

> q:=-1.6у-19:massa:=9.1е-31:V:=1е7:alpha:=80*Рi/180:

> Vx:=V*cos(alpha):Vy:=V*sin(alpha): Ex:=0:Ey:=0:Ez:=0: Bx:=0.1:By:=0:

Bz:=0:

Построим траекторию движения частиц в пространстве:

> with(DEtools):DEplot3d({sys},{x(t), y(t) ,z(t)},

t=0..2e-9, [[x(0)=0, D(x)(0)=Vx, у(0)=1, D(y)(0)=Vy, z(0)=0, D(z)(0)=0]],

stepsize=1e-11,orientation=[24,117]);

Полученная траектория представлена на рис. 11.24. Она имеет вид спирали в пространстве. При этом скорость движения частицы вдоль оси x неизменна, а вдоль осей у и z имеет характерную колебательную компоненту. Случай явно куда менее тривиальный, чем полет камня, описанный выше.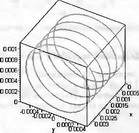

Рис. 11.24. Траектория движения частицы в магнитном поле

Мы можем найти аналитическое представление для траектории частицы в виде параметрически заданной (с параметром времени t) системы из трех уравнений:

>xyz:=dsolve({sys,х(0)=0,D(х)(0)=Vx,у(0)=0,D(у)(0)=Vy,z(0)=0, D(z)(0)=0}, (x(t), у(t), z(t)}, method=ldplace);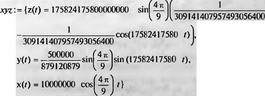

Моделирование движения заряженной частицы в пространстве с магнитным полем показывает, что для принятых для моделирования параметров решаемой задачи, движение частицы происходит по спиралеобразной траектории. Получен как график траектории движения частицы, так и аналитические уравнения, описывающие это движение.

Рассмотрим еще одну классическую задачу ядерной физики — разделение изотопов (атомов с одинаковым зарядом ядра, но разной массой). Документ с решением этой задачи представлен в файле izotop. Он реализует масс-спектроскопический метод.

Итак, пусть из точки А вылетают однозарядные ионы (q=e=1,6∙10^-19 Кл) разной массы (от 20 до 23 а.е.м.) и под разными углами в пределах от 80 до 100° к оси х в плоскости ху (рис. 11.25). Вдоль оси z приложено магнитное поле В=10^-2 Тл. Рассчитать траектории полета частиц. Будем надеяться, что это подскажет способ разделения изотопов.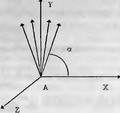

Рис. 11.25. Иллюстрация к методу разделения изотопов

Приступим к решению данной задачи. Сила Лоренца, действующая на движущуюся частицу F=q(E+[v, B]). Проекции векторного произведения [v, В] на оси х, у, z заданы выражениями:

[v, В]х = vy*Bz-vz*By [v, В]у = vz*Bx-vx*Bz [v, B]z = vx*By-vy*Bz

В соответствии с этим дифференциальные уравнения, описывающие траекторию полета частицы по осям х, у, z имеют вид:

> restart;

> sys:=diff(х(t),t$2)=q*(Ex+(diff(y(t), t) * Bz-

diff(z(t), t)*By))/massa,diff(y(t),t$2)=q*(Ey+(diff(z(t),t)* Bx-

diff(x(t),t)*Bz))/massa,diff(z(t),t$2)=q*(Ez+(diff(x(t),t) * By-

diff(y(t),t)*Bx))/massa;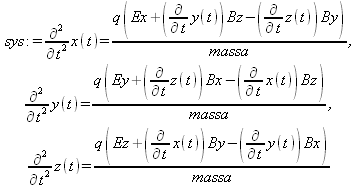

Зададим исходные числовые данные для расчета:

> q:=1.6e-19:V:=1e4:

> Vx:=V*cos(alpha): Vy:=V*sin(alpha): Ex:=0: Ey:=0: Ez:=0:

Bx:=0: By:=0: Bz:=1e-2:

Выполним решение составленной выше системы дифференциальных уравнений:

> xyz:=dsolve{(sys,х(0)=0,D(х)(0)=Vx,у(0)=0,D(у)(0)=Vy,

z(0)=0, D(z)(0)=0},{х(t), у(t), z(t)}, method=laplace):

> XX:=(massa,alpha)->.6250000000e25*massa*(sin(alpha)-

1.* sin(alpha)*cos(.1600000000e-

20 * t/massa)+cos(alpha)*sin(.1600000000e-20*t/massa));

> YY:=(massa,alpha)->.6250000000e25*massa*(-

1.*cos(alpha)+cos(alpha)*cos(.1600000000e-20*t/massa) + sin(alpha) * sin(.1600000000e-20*t/massa));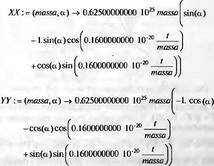

Построим графики решения:

> aem:=1.67e-27: ur:=3.14/180:

> plot([[XX(20*aem,80*ur), YY(20*aem,80*ur),

t=0..10e-5], [ХХ(20*aem,90*ur), YY(20*aem,90*ur),

t=0..10e-5], XX(28*aem, 80*ur), YY(28*aem, 80*ur),

t=0..10e-5], [XX(28*aem,90*ur),YY(28*aem,90*ur),

t=0..10e-5], [XX(24*aem,80*ur), YY(24*aem,80*ur),

t=0..10e-5], [XX(24*aem,90*ur), YY(24*aem,90*ur),

t=0..10e-5]], view=[0..0.65,0..0.65],

color=[red,red,blue,blue,black,black],labels=[x,y]);

Эти графики показаны на рис. 11.26.

Рис. 11.26. Траектории движения частиц

Полученные графики (рис. 11.26) наглядно показывают на одну из возможностей разделения изотопов. Как говорится, осталось подставить «стаканчик» в нужное место для ловли нужных изотопов. Разумеется, это только изложение идеи одного из методов разделения изотопов. Увы, на практике приходится использовать сложнейшие и дорогие физические установки для решения этой актуальной задачи.

Одним из фундаментальных доказательств существования ядра у атомов стал опыт с бомбардировкой тонкой фольги из металла альфа-частицами с высокой энергией. Если бы «массивных» ядер не существовало, то альфа-частицы должны были бы спокойно пролетать тонкую фольгу, практически не отклоняясь. Однако, как физики и ожидали, некоторая часть частиц испытывала сильное отклонение и даже поворачивала назад. Очевидно, что имели место отскоки (упругие столкновения) с малыми, но массивными ядрами металла фольги.

В нашем распоряжении, увы (а может быть и к счастью), нет ускорителя альфа-частиц. Так что мы, не опасаясь облучения и очередной Чернобыльской катастрофы, сможем смоделировать это интереснейшее физическое явление с помощью математической системы Maple. Причем спокойно сидя перед своим домашним компьютером и глубокомысленно наблюдая за траекториями полета альфа-частиц (см. файл rasseiv).

Итак, пусть в нашем теоретическом опыте альфа-частицы с энергией 4 МэВ рассеиваются тонкой золотой фольгой. Рассчитать траекторию частицы, приближающейся к ядру атома Au. Прицельное расстояние р равно 2∙10^-15 м.

Приступим к решению задачи и зададим вначале систему дифференциальных уравнений для траектории альфа-частицы:

> restart;

> sys:=diff(x(t),t$2)=q1*q2*x(t)/(4*Pi*E0*massa*

(x(t)^2+у(t)^2)^(3/2)), diff(y(t),t$2)=q1*q2*y(t)/(4*Pi*E0*

massa*(x(t)^2+y(t)^2)^(3/2));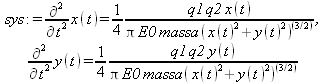

Введем исходные числовые данные для вычислений:

> q1:=2*1.6е-19:q2:=79*1.6е-19:massa:=4*1.67е-27:Е0:=8.85е-12:

а:=4е-13:р:=5е-15:Т:=4е6*1.6e-19:V0x:=sqrt(2*T/massa):

Создадим графическую структуру решения нашей системы дифференциальных уравнений для нескольких расчетных отклонений линии движения альфа-частицы от центра ядра атома, находящегося на ее пути:

> with(DEtools):ss:=DEplot({sys},{y(t),x(t)}, t=0..7e-20, [[x(0)=-a, D(x)(0)=V0x, y(0)=p, D(y)(0)=0],

[х(0)=-а, D(х)(0)=V0x, y(0)=р*4, D(y)(0)=0], [х(0)=-а, D(х)(0)=V0x, y(0)=p*8, D(y)(0)=0], [х(0)=-а, D(x)(0)=V0x, y(0)=р*12, D(y)(0)=0], [х(0)=-а, D(х)(0)=V0x, y(0)=p*16, D(y)(0)=0], [х(0)=-а, D(х)(0)=V0x, y(0)=р*20, D(y)(0)=0], [х(0)=-а, D(х)(0)=V0x, y(0)=р*24, D(y)(0)=0], [х(0)=-а, D(х)(0)=V0x, y(0)=р*28, D(y)(0)=0]],

х(t)=-а..a, scene=[x(t),у(t)], stepsize=1e-21, linecolor=black):

> with(plottools): yy:=circle([0,0],2E-14,color=red,thickness=2) : Warning, the name translate has been redefined

Построим центр ядра (кружок со знаком +) и траектории альфа-частиц

> ss2:=PLOT(TEXT([0,-0.3а-14],` +`), FONT(HELVETICA, OBLIQUE,14)):

Осталось построить график траекторий движения альфа-частиц вблизи центра атома

> with(plots):

Warning, the name chargecoords has been redefined

> display([ss,yy,ss2],title=`Рассеивание а-частиц`, axes=framed);

График траекторий движения альфа-частиц вблизи ядра представлен на рис. 11.27. Этот график настолько нагляден, что не требует пояснения.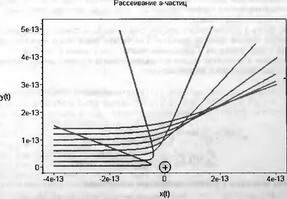

Рис. 11.27. Траектории движения альфа-частиц вблизи ядра атома

Моделирование движения альфа-частиц вблизи малого и «массивного» ядра атома дают наглядное представление о математической и физической сути данного опыта. Надо лишь помнить, что нельзя нацеливать быстро летящие альфа-частицы прямо в центр ядра. Более сложные, чем приведенные, расчеты показывают, что при этом альфа-частица настолько близко подходит к ядру, что надо учитывать новые факторы, возникающие при близком взаимодействии. Они могут привести к тому, что частица будет поглощена ядром. Но, это уже тема нового разговора, выходящего за рамки данной книги.

Нужно ли применять системы компьютерной математики для анализа, расчета и моделирования электронных схем? Ответ на этот вопрос не так прост, как кажется с первого взгляда С одной стороны к услугам пользователя компьютера сейчас имеется ряд программ схемотехнического моделирования, например Micro-CAP, Electronics Workbench, PSpice, Design Labs и др., автоматически составляющих и решающих большие системы уравнений состояния электронных схем и моделирующих работу бесчисленного множества электронных схем без кропотливого «ручного» составления уравнений.

Но, с другой стороны, анализ схем в таких программах настолько автоматизирован, что начисто теряется его физическая и математическая сущность. Это не так уж страшно, когда моделируются типовые схемы на давно известных, или скорее просто хорошо знакомых, электронных приборах. Но, это явно плохо, когда объектом исследования и моделирования являются новые нетрадиционные схемы на новых или малоизвестных приборах или когда знание физических и математических основ работы таких схем принципиально необходимо. Например, при изучении их в вузах и университетах. В этом случае применение систем компьютерной математики не только возможно, но и принципиально необходимо.

Вернемся к линейным системам и рассмотрим еще один полезный метод расчета электрических цепей — с помощью интеграла Дюамеля. При нем можно рассчитать временную зависимость выходного напряжения u2(t) цепи по известному входному сигналу u1(t) и переходной характеристики цепи a(t). Возьмем в качестве первого классического примера дифференцирующую RC-цепь и вычислим ее реакцию на экспоненциально нарастающий перепад напряжения. Соответствующие расчеты приведены на рис. 11.28.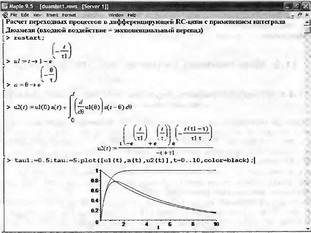

Рис. 11.28. Расчет реакции дифференцирующей цепи на экспоненциальный перепад напряжения

Рис. 11.28 представляет начало документа, в котором выполнен указанный выше расчет. Представлены заданные зависимости uI(t) и a(t), аналитическое выражение для интеграла Дюамеля (одна из 4 форм) и аналитическое выражение для искомой зависимости u2(t). Пока последнее выражение довольно простое. В конце этого фрагмента документа построены графики зависимостей u1(t), a(t) и u2(t).

Окончание документа, представленное на рис. 11.29, демонстрирует расчет на основе интеграла Дюамеля реакции дифференцирующей RC-цепи на экспоненциально затухающий синусоидальный сигнал u1(t).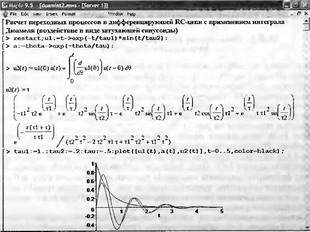

Рис. 11.29. Расчет реакции дифференцирующей цепи на синусоидальный сигнал с экспоненциально уменьшающейся амплитудой

Обратите внимание на то, что выражение для u2(t), получаемое с помощью интеграла Дюамеля, стало намного сложнее. Тем не менее, получено как аналитическое выражения для реакции цепи u2(t), так и графики u1(t), a(t) и u2(t). Они показаны внизу графика.

Теперь рассмотрим проектирование аналогового полосового фильтра-усилителя на операционном усилителе (файл af), схема которого приведена на рис. 11.30. Сам операционный усилитель будем считать идеальным.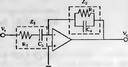

Рис. 11.30. Схема полосового фильтра на интегральном операционном усилителе

Подготовимся к расчету фильтра:

> restart:

Зададим основные уравнения, описывающие работу усилителя на малом сигнале:

> Vo := (-Z2/Z1)* Vi;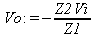

> Z1 := R3 + 1/(I*omega*C3);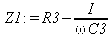

> Z2 := R4*1/(I*omega*C4) / (R4 + 1/(I*omega*C4));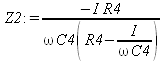

Введем круговую частоту

> omega := 2*Pi*f;

Найдем в аналитическом виде коэффициент передачи фильтра и его фазочастотную характеристику как функции от частоты:

> gain := abs(evalc(Vo/Vi));

> phase := evalc(op(2,convert(Vo/Vi,polar)));

Эти выражения, несмотря на простоту схемы усилителя, выглядят довольно сложно, что, однако, ничуть не мешает использовать их для выполнения расчетов. Зададим конкретные значения параметров:

> R3 := 1000:

> R4 := 3000:

> C3 := 0.08*10^(-6):

> С4 := 0.01*10^(-6):

Построим АЧХ фильтра как зависимость коэффициента передачи в децибелах (dB) от частоты f в Гц:

> plot([log10(f), 20*logl0(gain), f=10..50000],

color=black, title=`Коэффициент передачи dB как функция от логарифма частоты f в Гц`);

Эта характеристика представлена на рис. 11.31. Здесь полезно обратить внимание на то, что спад усиления на низких и высоких частотах происходит довольно медленно из-за малого порядка фильтра.

Рис. 11.31. АЧХ фильтра на операционном усилителе

Далее построим фазочастотную характеристику фильтра как зависимость фазы в радианах от частоты f в Гц:

> plot([log10(f), phase, f=10..50000], color=black, title= `Фаза в радианах как функция логарифма частоты`);

Фазочастотная характеристика (ФЧХ) фильтра показана на рис. 11.32.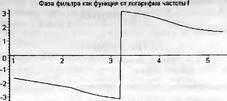

Рис. 11.32. ФЧХ фильтра на операционном усилителе

На ФЧХ фильтра можно заметить характерный разрыв, связанный с превышением фазовым углом граничного значения π. Такой способ представления фазового сдвига общепринят, поскольку его изменения стремятся вписать в диапазон от -π до π.

Основной недостаток аналоговых активных фильтров, подобных описанному выше, заключается в их малом порядке. Его повышение, за счет применения многих звеньев низкого порядка, ведет к значительному повышению габаритов фильтров и их стоимости. От этого недостатка свободны современные цифровые фильтры, число ячеек которых N даже при однокристальном исполнении может достигать десятков и сотен. Это обеспечивает повышенную частотную селекцию.

Спроектируем фильтр N+1-го порядка класса FIR (Finite Impulse Response или с конечной импульсной характеристикой). Документ, решающий эту задачу, представлен в файле fir.

Каждая из N ячеек временной задержки фильтра удовлетворяет следующей зависимости выходного сигнала у от входного х вида: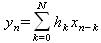

Подключим пакет расширения plots, нужный для графической визуализации проектирования:

> restart:with(plots):

Warning, the name changecoords has been redefined

Зададим исходные данные для проектирования полосового цифрового фильтра, выделяющего пятую гармонику из входного сигнала в виде зашумленного меандра с частотой 500 Гц:

> N := 64: # Число секций фильтра (на 1 меньше порядка фильтра)

> fs := 10000: # Частота квантования

> fl := 2300: # Нижняя граничная частота

> fh := 2700: # Верхняя граничная частота

> m := 10: # 2^m > N - число точек для анализа

Вычислим:

> Т := 2^m-1;

> F1 : = evalf(fl/fs);

> F2 := evalf(fh/fs);

> Dirac(0) := 1: # Функция Дирака

> fp1:=2*Pi*F1: fp2:=2*Pi*F2:

Зададим характеристику полосового фильтра:

> g : = (sin(t*fp2)-sin(t*fp1))/(t*Pi);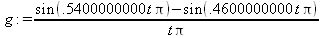

Вычислим FIR коэффициенты для прямоугольного окна фильтра

> С := (n) -> limit(g,t=n): h := aray(0..N): N2:=N/2:

> for n from 0 to N2 do h[N2-n]:= evalf(C(n)); n[N2+n] :=

h[M2-n]; od:

Определим массивы входного x(n) и выходного y(n) сигналов:

> х := array(-N..Т): y:= array(0..T):

Установим значение x(n) равным 0 для времени меньше 0 и 1 для времени t>=0.

> for n from -M to -1 do x[n] := 0; od:

> for n from 0 to T do x[n] := Dirac(n); od:

Вычислим временную зависимость для выходного сигнала.

> for n from 0 to Т do y[n] := sum(h[k]*x[n-k], k=0..N); od:

Построим график импульсной характеристики фильтра, отражающей его реакцию на сигнал единичной площади с бесконечно малым временем действия:

> р := [seq{[j/fs, y[j]], j=0..Т)]:

> plot(р, time=0..3*N/fs, labels=[time,output], axes=boxed,

xtickmarks=4, title=`Импульсная характеристика фильтра`, color=black);

Он показан на рис. 11.33. Нетрудно заметить, что эта характеристика свидетельствует об узкополосности фильтра, поскольку его частоты fl и fh различаются не сильно. В этом случае полосовой фильтр по своим свойствам приближается к резонансному, хотя само по себе явление резонанса не используется.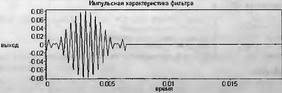

Рис. 11.33. Импульсная характеристика цифрового фильтра

Вычислим АЧХ фильтра, используя прямое преобразование Фурье. Оно, после подготовки обрабатываемых массивов, реализуется функцией FFT:

> ro := array(1..Т+1):io := array(1..Т+1):

> for n from 0 to T do ro[n+1] := y[n]; io[n+1] := 0; od:

> FFT(m,ro,io):

Построим график АЧХ фильтра:

> р := [seq( [j*fs/(Т+1),abs(ro[j + 1]+io[j + 1]*I)], j=0..T/2)]:

> plot(p, frequency=0..fs/2, labels=[frequency,gain], title=`AЧX

фильтра`, color=black);

Он представлен на рис. 11.34. Нетрудно заметить, что и впрямь АЧХ фильтра напоминает АЧХ резонансной цепи — она имеет вид узкого пика. Вы можете легко проверить, что раздвижением частот fl и fh можно получить АЧХ с довольно плоской вершиной и резкими спадами (говорят, что такая характеристика приближается к прямоугольной).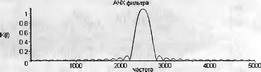

Рис. 11.34. АЧХ цифрового полосового фильтра

Теперь приступим к тестированию фильтра. Зададим входной сигнал в виде зашумленного меандра с частотой 500 Гц и размахом напряжения 2 В:

> l := round(fs/2/500):

> for n from 0 by 2*1 to T do

>  for n2 from 0 to l-1 do

>   if n+n2 <= T then

>    x[n+n2] := evalf(-l+rand()/10^12-0.5);

>   fi;

>   if n+n2+1 <= T then

>    x[n+n2+1] := evalf(1+rand()/10^12-0.5);

>   fi;

>  od:

> od:

Временная зависимость синтезированного входного сигнала представлена на рис. 11.35.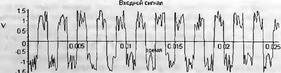

Рис. 11.35. Синтезированный входной сигнал

Вычислим реакцию фильтра на входной сигнал:

> for n from 0 to Т do

>  y[n] : = sum(h[k]*х[n-k], k=0..N);

> od:

Построим график выходного сигнала.

> р := [seq([j/fs, x[j]], j=0..T)]: q:=[seq([j/fs, y[j]], j=0..T)]:

> plot(p, time=0..T/fs/4, labels=[time,volts], title= `Входной сигнал`, color=black);

> plot(q, time=0..T/fs/4, labels=[time, volts], title=`Выгодной сигнал`, color=black);

Временна́я зависимость выходного сигнала показана на рис. 11.36. Нетрудно заметить, что, в конце концов, выходной сигнал вырождается в пятую гармонику входного сигнала, но этому предшествует довольно заметный переходной процесс. Он связан с узкополосностью данного фильтра.

Рис. 11.36. Временна́я зависимость выходного сигнала цифрового фильтра

Вычислим спектры входного и выходного сигналов, подготовив массивы выборок сигналов и применив прямое преобразование Фурье с помощью функции FFT:

> ri := array(1..Т+1): ii := array(1..Т+1):

> for n from 0 to T do

>  ri[n+1] := x[n]*2/T; ii[n+1] := 0;

>  ro[n+1] := y[n]*2/T; io[n+1] := 0;

> od:

> FFT(m, ri, ii): FFT(m,ro,io):

Построим график спектра входного сигнала, ограничив масштаб по амплитуде значением 0.5 В:

> р := [seq([j*fs/(T+1), abs(ri[j+1]+ii[j+1]*I)], j=0..T/2)]:

> q := [seq([j*fs/(T+1), abs(ro[j+1]+io[j+1]*I)], j=0..T/2)] :

> plot(p, frequency=0..fs/2, y=0..0.5, labels=[частота, V],

titles=`Частотный спектр входного сигнала`, color=black);

Этот график представлен на рис. 11.37. Из него хорошо видно, что спектральный состав входного сигнала представлен только нечетными гармониками, амплитуда которых убывает по мере роста номера гармоники. Пятая гармоника на частоте 2500 Гц находится посередине полосы пропускания фильтра, ограниченной граничными частотами фильтра 2300 и 2700 Гц. Заметны также беспорядочные спектральные линии шума сигнала в пределах полосы прозрачности фильтра.

Рис. 11.37. Спектрограмма входного сигнала

Теперь построим график спектра выходного сигнала:

> plot(q, frequency=0..fs/2, y=0..0.5, labels=[частота, V],

title=`Частотный спектр выходного сигнала`, color=black);

Он представлен на рис. 11.38. Хорошо видно эффективное выделение пятой гармоники сигнала и прилегающей к ней узкой полосы шумового спектра.

Рис. 11.38. Спектрограмма выходного сигнала цифрового фильтра

Приведенные данные свидетельствуют, что спроектированный фильтр полностью отвечает заданным требованиям и обеспечивает уверенное выделение пятой гармоники зашумленного меандра. По образу и подобию данного документа можно выполнить проектирование и других видов цифровых фильтров.

А теперь займемся моделированием явно нелинейной цепи. Выполним его для цепи, которая состоит из последовательно включенных источника напряжения Es, резистора Rs, индуктивности L и туннельного диода, имеющий N-образную вольт-амперную характеристику (ВАХ) — см. файл tdc. Туннельный диод обладает емкостью С, что имитируется конденсатором С, подключенным параллельно туннельному диоду.

Пусть ВАХ реального туннельного диода задана выражением:

> restart;

> А:=-3: а:=10: В:=1*10^(-8): b:=20:

> Id:=Ud->A*Ud*exp(-a*Ud)+B*(exp(b*Ud-1));

Построим график ВАХ:

> plot(Id(Ud), Ud=-.02..0.76, color=black);

Этот график представлен на рис. 11.39. Нетрудно заметить, что ВАХ туннельного диода не только резко нелинейна, но и содержит протяженный участок отрицательной дифференциальной проводимости, на котором ток падает с ростом напряжения на диоде. Это является признаком того, что такая цепь способна на переменном токе отдавать энергию во внешнюю цепь и приводить к возникновению колебаний в ней различного типа.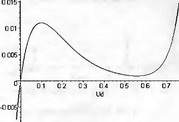

Рис. 11.39. ВАХ туннельного диода

Работа цепи описывается системой из двух дифференциальных уравнений:

di/dt= (Es-i(t) * Rs-u(t))/L

du/dt= (i(t)-Id(u(t))/C

Пусть задано Es=0,35 В, Rs=15 Ом, C=10∙10^-12, L=30∙10^-9 и максимальное время моделирования tm=10∙10^-9. Итак, задаем исходные данные:

> Es: = .35: Rs:=15: C:=10*10^(-12): L:=30*10^(-6): tm:=10*10^(-9):

Составим систему дифференциальных уравнений цепи и выполним ее решение с помощью функции dsolve:

> se:=diff(i(t),t) = (Es-i(t)*Rs-u(t)) /L,

difff(u(t), t) = (i(t)- Id(u(t))) / С;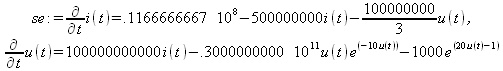

> F:=dsolve({se, i(0)=0, u(0)=0}, {i(t),u(t)}, type=numeric,

method-=classiccal, stepsize=10^(-11), output=listprocedure);

Поскольку заведомо известно, что схема имеет малые значения L и С мы задали с помощью параметров достаточно малый шаг решения для функции dsolve — stepsize=10^(-11) (с). При больших шагах возможна численная неустойчивость решения, искажающая форму колебаний, получаемую при моделировании. Используя функции odeplot и display пакета plots построим графики решения в виде временных зависимостей u(t) и 10∙i(t) и линии, соответствующей спряжению Es источника питания:

> gu:=odeplot(F,[t, u(t)], 0..tm, color=black,

labels=[`t`, `u(t),10*i(t)`]):

> gi:=odeplot(F, [t, 10*i (t)], 0..tm, color=black):

> ge:=odeplot(F, [t,Es], 0..tm, color=red):

> display(gu, gi, ge);

Эти зависимости представлены на рис. 11.40. Из них хорошо видно, что цепь создает автоколебания релаксационного типа. Их форма сильно отличается от синусоидальной.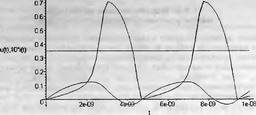

Рис. 11.40. Временные зависимости напряжения на туннельном диоде и тока

Решение можно представить также в виде фазового портрета, построенного на фоне построенных ВАХ и линии нагрузки резистора Rs:

> gv:=plot({Id(Ud), (Es-Ud)/Rs), Ud=-.05..0.75, color=black, labels=[Ud,Id]):

> gpp:=odeplot(F,[u(t),i(t)], 0..tm,color=blue):

> display(gv,gpp);

Фазовый портрет колебаний показан на рис. 11.41.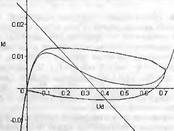

Рис. 11.41. Фазовый портрет колебаний на фоне ВАХ туннельного диода и линии нагрузки резистора Rs

О том, что колебания релаксационные можно судить по тому, что уже первый цикл колебаний вырождается в замкнутую кривую — предельный цикл, форма которого заметно отличается от эллиптической (при эллиптической форме фазового портрета форма колебаний синусоидальная).

Итак, мы видим, что данная цепь выполняет функцию генератора незатухающих релаксационных колебаний. Хотя поставленная задача моделирования цепи на туннельном диоде успешно решена, в ходе ее решения мы столкнулись с проблемой обеспечения малого шага по времени при решении системы дифференциальных уравнений, описывающих работу цепи. При неудачном выборе шага можно наблюдать явную неустойчивость решения.

Еще один пример, наглядно иллюстрирующий трудности моделирования существенно нелинейных систем и цепей, описывающихся нелинейными дифференциальными уравнениями — детектирование амплитудно-модулированных сигналов. Простейший детектор таких сигналов представляет собой полупроводниковый диод, через который источник сигнала подключается к параллельной RC-цепи, выполняющей роль простого фильтра (без конденсатора С результат детектирования имел бы вид обрезанного снизу сигнала).

Диод имеет резко нелинейную вольт-амперную характеристику. Ток через него равен:

где v — напряжение на диоде, I0 — малый обратный ток диода.

Экспоненциальная зависимость тока от напряжения порождает большие трудности в моделировании этого крайне простого устройства. На обратной ветви вольт-амперной характеристики диода его дифференциальное сопротивление очень велико (многие МОм), а на прямой ветви напротив мало (десятки и даже единицы Ом). Это порождает жесткость дифференциального уравнения, описывающего детектор и требует применения численных методов решения жестких дифференциальных уравнений. Заметим, что аналитического решения данная задача не имеет, ввиду нелинейности дифференциального уравнения, описывающего работу детектора.

С учетом этих обстоятельств, построен документ, представленный на рис. 11.42, и решающий данную задачу. В нем определено исходное дифференциальное уравнение и содержится его решение при заданных исходных данных — детектируется амплитудно-модулированный сигнал с амплитудой Um=5 В (размерные величины опущены), частотой несущей f=20 кГц, частотой модуляции F=1000 Гц и коэффициентом модуляции m=0.5. Определена вольт-амперная характеристика диода при I0=1 мкА и построен ее график. Далее выполнено решение нелинейного дифференциального уравнения при R=100 Ом и С=5 мкФ с помощью функции dsolve и построение графиков исходного сигнала и сигнала на выходе детектора (утолщенной линией).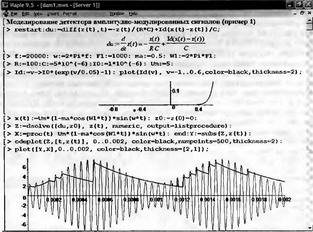

Рис. 11.42. Моделирование детектора амплитудно-модулированного сигнала (пример 1)

Результат моделирования не очень удовлетворителен. В начале процесса виден рост выходного сигнала в промежутках между положительными полуволнами входного сигнала. Это противоречит физике процессов в детекторе — на этих участках конденсатор С может только разряжаться через резистор R и сигнал должен всегда падать. Затем ситуация еще хуже — некоторые полуволны входного сигнала, заметно превышающие по уровню входной сигнал явно пропущены. Все эти тонкости следствие грубого сбоя в решении нелинейного дифференциального уравнения и обусловлены неудачным автоматическим выбором методов решения данного дифференциального уравнения.

Любопытно поведение выходного сигнала и при его спаде при малой амплитуде входного сигнала. Этот эффект может иметь физическую природу — при большой выходной сигнал спадает медленно и отрывается от верхушек полуволн входного сигнала. Устранить этот нежелательный для детектирования эффект можно уменьшением R или С.

На рис. 11.43 показан пример более корректного моделирования. В нем в параметрах функции dsolve введена опция stiff=true, указывающая на необходимость применения методов решения жестких дифференциальных уравнений. Кроме того, уменьшено значение С=2мкФ. Моделирование теперь идет корректно, но выходной сигнал на спаде моделирующего сигнала не очень четко отслеживает последний. Это указывает, что постоянная времени RC все еще велика.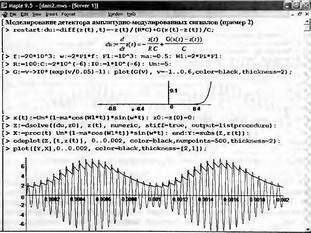

Рис. 11.43. Моделирование детектора амплитудно-модулированного сигнала (пример 2)

Рассмотрим еще один пример, представленный на рис. 11.44. Здесь значение емкости С конденсатора на выходе детектора уменьшено до 1 мкФ. Кроме того, в функции dsolve явно указан метод Розенброка — один из лучших методов решения жестких дифференциальных уравнений. Кроме того, во избежание числовой неустойчивости, возможной даже при этом методе, решение задается с заданной абсолютной и относительной погрешностью 10^-4. Уменьшение погрешности лучше устраняет числовую неустойчивость, но ведет к увеличению времени моделирования.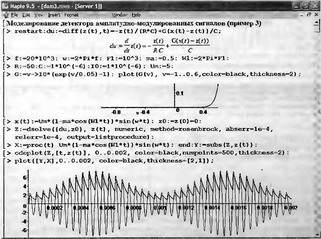

Рис. 11.44. Моделирование детектора амплитудно-модулированного сигнала (пример 3)

На этот раз как само моделирование, так и «работа» детектора происходят безупречно в соответствии с принципом действия этого устройства. Этот не означает, что так и будет при любых параметрах устройства. Читатель может убедиться в этом сам. А все сказанное говорит о том, что даже при моделировании такого простого устройства возможности Maple не безупречны. Без четкого понимания физики работы моделируемого устройства можно получить не только неточные данные, но и порой данные, противоречащие физике работы устройств.

В некоторых случаях необходим учет заданных, чаще всего постоянных, граничных условий. Типичным примером этого является расчет временной и координатной зависимости температуры нагретого стержня, запрессованного концами в области с постоянной температурой. Это соответствует решению одной из типовых задач термодинамики.

Рисунок 11.45 показывает начало документа Maple 9 решающего данную задачу. На нем дана математическая формулировка задачи, задание и решение дифференциального уравнения в частных производных с нулевыми граничными условиями. Температура вдоль стержня при t=0 задана выражением g(x).

Рис. 11.45. Начало документа, вычисляющего распределение температуры вдоль стержня с нулевой температурой на концах

Рис. 11.46 показывает результаты моделирования для задачи, представленной на рис. 11.45. Верхний рисунок анимационный и представляет начальный кадр — распределение температуры вдоль оси х при t=0. Если пустить анимацию можно наблюдать в динамике процесс остывания стержня. Наглядное представление этого процесса в виде трехмерного графика показано ниже. Он представляет собой сплошной набор линий u(х, t) в различные моменты времени t. Нетрудно заметить, что отклонение температуры от 0 падает по мере роста t.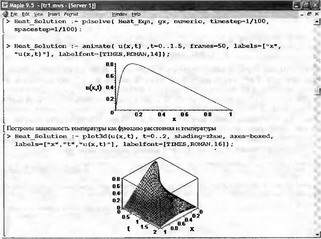

Рис. 11.46. Представление зависимости температуры u(х) в разные моменты времени — сверху в виде анимационного рисунка, снизу в виде трехмерного графика

Рис. 11.47 показывает задание процедуры для вычисления значения температуры в численном виде для заданных x и t, а также дает еще один пример вычисления зависимости u(х,t) и построения анимационного графика этой зависимости. На графике рис. 11.47 представлен конечный кадр анимации.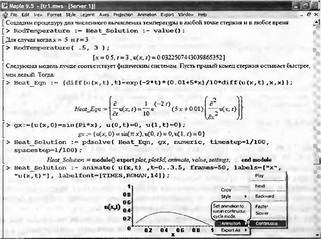

Рис. 11.47. Конец документа, представленного рис. 11.45 и 11.46

Еще один классический пример решения дифференциального уравнения с заданными граничными условиями это моделирование колебаний струны, зажатой на концах. Рис. 11.48 демонстрирует начало документа, выполняющего такое моделирование (файл coord). На нем представлена формулировка задачи, задание дифференциального уравнения и граничных условий для его решения.

Рис. 11.48. Начало документа моделирования колебаний струны

На рис. 11.49 показан первый случай моделирования — струна оттянута в середине, так что распределение ее отклонения от расстояния х имеет характер вначале нарастающей линейно, а затем линейно уменьшающейся зависимости. Анимационные кадр второй по счету показывает, что после отпускания струны в центре появляется плоский участок, который расширяется и перемещается вниз. Формируется один период колебаний (положительный и отрицательный полупериоды).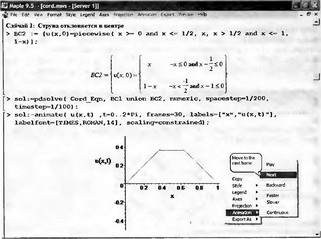

Рис. 11.49. Моделирование колебаний струны, оттянутой вверх посередине, после ее отпускания

Рисунок 11.50 показывает второй пример моделирований. На этот раз струна деформирована по синусоидальному закону, так что на ней укладывается три периода синусоиды. С момента начала моделирования можно наблюдать ее колебания, в ходе которых амплитуда синусоиды периодически то уменьшается, то увеличивается — режим стоячих волн. На рисунке представлен конечный кадр анимации.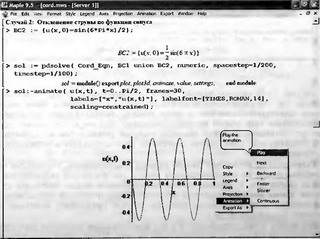

Рис. 11.50. Моделирование колебаний струны по синусоидальному закону

Эту модель можно использовать и для моделирования колебания двух струн с более сложным характером начальной деформации. Такой случай представлен на рис. 11.51. Здесь представлен промежуточный кадр анимации.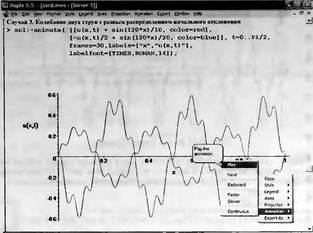

Рис. 11.51. Пример моделирования колебаний двух струн

В главе 6 отмечались возможности пакета расширения системы Maple Matlab, дающего доступ к некоторым функциям мощной матричной системы MATLAB. Там мы рассмотрели применение функций линейной алгебры.

Среди небольшого числа доступных функций системы MATLAB в пакете Matlab нельзя не выделить особо функции быстрого прямого и обратного преобразований Фурье. В системе MATLAB эти функции реализуют наиболее эффективные алгоритмы быстрого преобразования Фурье (БПФ), обеспечивающие решение крупноразмерных задач (например, обработки сигналов, представленных векторами и матрицами больших размеров) в десятки раз быстрее, чем при обычных методах выполнения преобразований Фурье.

Покажем возможность применения БПФ на ставшем классическим примере — выделении спектра полезного сигнала на фоне сильных помех (файл dnmatlab). Зададим некоторый двухчастотный сигнал, имеющий 1500 точек отсчета:

> num := 1500:

Time := [seq(.03*t, t=1..num)]:

data := [seq((3.6*cos(Time[t]) + cos(6*Time[t])), t=1..num)):

plots[pointplot](zip((x,y)->[x,y],Time,data), style=line);

График сигнала представлен на рис. 11.52.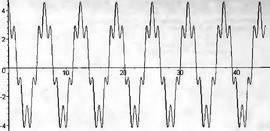

Рис. 11.52. График исходного сигнала

Теперь с помощью генератора случайных чисел наложим на этот сигнал сильный «шум» (слово «шум» взято в кавычки, поскольку речь идет о математическом моделировании шума, а не о реальном шуме физической природы):

> tol := 10000: r := rand(0..tol):

noisy_data := [seq(r()/(tol)*data[t], t=1..num)]:

plots[pointplot](zip((x,y)->[x,y],Time,noisy_data), style=line);

Нетрудно заметить, что теперь форма сигнала настолько замаскирована шумом (рис. 11.53), что можно лишь с трудом догадываться, что сигнал имеет периодическую составляющую малой амплитуды. Эта высокочастотная составляющая сигнала скрыта шумом.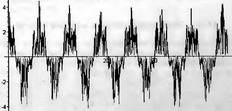

Рис. 11.53. Временная зависимость сигнала с шумом

Подвергнем полученный сигнал (в виде временной зависимости) прямому преобразованию Фурье, реализованному функцией fft:

> ft := fft(noisy_data):

> VectorOptions(ft, datatype);

Эта операция переводит задачу из временного представления сигнала в частотное, что позволяет использовать частотные методы анализа сигнала. Выделим, к примеру, действительную и мнимую части элементов вектора ft и проверим его размер:

> real_part := map(Re, ft): imag_part := map(Im, ft):

> dimensions(ft);

Теперь выполним обычные операции вычисления спектра и зададим построение графика частотного спектра мощности сигнала:

> setvar("FT", ft);setvar("n", num);

> evalM("result = FT.*conj(FT)/n");

> pwr := getvar("result"):

> VectorOptions(pwr, datatype);

> pwr_list := convert(pwr, list):

> pwr_points := [seq([(t-1)/Time[num], pwr_list[t]], t=1..num/2)]:

> plots[pointplot](pwr_points, style=line);

Спектрограмма сигнала представлена на рис. 11.54.

Рис. 11.54. Спектрограмма сигнала

Из нее отчетливо видно, что сигнал представлен двумя частотными составляющими с разной амплитудой. Таким образом, задача четкого выделения полезных компонент частотного спектра из зашумленного сигнала с применением средств системы MATLAB успешно решена.

Выше было не раз показано, что система Maple позволяет выполнять моделирование различных колебательных систем. Однако более эффективнее средства для такого моделирования содержатся в системе MATLAB. В частности, к ним относится решатель дифференциальных уравнений, вводимый функцией ode45. Ниже на простом примере мы рассмотрим организацию совместной работы систем Maple 9.5 и MATLAB 7 SP2 (это новейшая версия данной системы) на примере моделирования механического осциллятора (маятника).

Рис. 11.55 показывает документ Maple в котором решается эта задача. Уравнение маятника записывается средствами Maple в виде файла oscil.m в формате М-файлов системы MATLAB. Записываются также системные переменные, задающие массу маятника М, его затухание С и упругость K. Затем с помощью функции ode45 (решение ОДУ методом Рунге-Кутта-Фельберга порядка 4–5) находится временная зависимость отклонения маятника. Она построена внизу рисунка и отражает типичные затухающие синусоидальные колебания с заданными граничными условиями.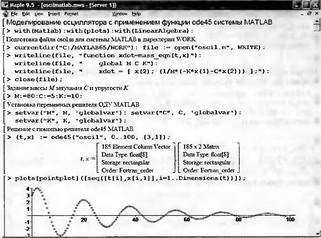

Рис. 11.55. Пример моделирования механического осциллятора в системе Maple + MATLAB

Разумеется, для такой относительно простой задачи привлечение такой мощной и громоздкой системы как MATLAB имеет только познавательный смысл. Эта задача, что было показано выше, легко решается средствами системы Maple. Однако технология совместного использования новейших систем Maple 9.5/10 и MATLAB 7.0 SP2 на этом примере хорошо видна и может использоваться пользователями для решения существенно более сложных задач математического моделирования

Рассмотрим хорошо известный физический эффект Доплера, возникающий при движении источника звука с частотой f_u, относительно приемника звука. При этом меняется частота звука, воспринимаемая приемником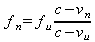

Будем считать приемник звука неподвижным, т.е. v_n=0, а источник перемещающимся со скоростью v_u. Скорость звука с на частоте 440 Гц составляет около 340 м/с. Движение в направлении распространения звуковой волны соответствует положительной скорости, а в противоположном — отрицательной. Описанный ниже документ находится в файле dopier (переработанный пример Sylvain Muise размещенный на Интернет-сайте корпорации MapleSoft).

Ниже представлена процедура позволяющая создавать анимационные эффекты перемещения источника звука (маленькая окружность) с разной скоростью и наблюдать картину создания и распространения звуковых волн:

> restart:with(plots):with(plottools):

> wave := proc(n, initSpeed, finalSpeed)

 local i, li, j, circles, se, source, slope:

 slope := (finalSpeed - initSpeed) / n:

 for i from 0 to n*4 do

  li := NULL:

  for j from 1 to n do

   if i > (j-1)*4 then

    circles[j][i] := circle([initSpeed * (j-1) + 0.5 * slope*(j-1)^2, 0], (i-(j-1)*4) / 4):

    li := circles[j][i], li:

   end if:

  end do:

  source := point([initSpeed * i/4 + 0.5 * slope * (1/4)^2, 0], @KOD = color=blue, symbol=circle, symbolsize=12):

  animation||i := display([li, source]):

 end do:

 se := animation || (0..n*4):

end proc:

В этой процедуре n задает число отображаемых волн, initSpeed и finalSpeed — начальная и конечная скорость движения источника звука. Разумеется, наблюдаемая на экране скорость движения звуковых волн намного меньше реальной с тем, чтобы мы могли воспринять это движение и осознать смысл представленных кадров анимации.

Для наблюдения эффекта создания и движения звуковых волн при неподвижном источнике звука исполним команды:

> wave1 := wave(10,0,0):

> display(wave1,insequence=true,scaling=constrained, axes=none);

Мы увидим рисунок в виде маленького кружка в центре — это источник звука. Пустив анимацию можно наблюдать эффект создания звуковых волн в виде ряда концентрических окружностей с увеличивающимся диаметром — рис. 11.56.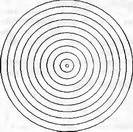

Рис. 11.56. Картина звуковых волн от неподвижного источника звука

Теперь рассмотрим случай, когда источник звука перемещается со скоростью, меньшей скорости звука:

> wave2 := wave(10,0.5,0.5):

> display(wave2,insequence=true,scaling=constrained, axes=none);

В этом случае мы наблюдаем разрежение звуковых волн после источника звука и их сжатие перед источником — рис. 11.57. Это означает изменение длины волны звуковых колебаний — случай, который многие из нас наблюдали, когда поезд с включенной сиреной проносится мимо нас и удаляется.

Рис. 11.57. Картина звуковых волн от источника звука, перемешаемого со скоростью меньше скорости звука

Современные реактивные самолеты легко достигают скорости звука и могут даже превысить ее. Это делает интересным случай движения источника звука со скоростью звука. Для наблюдения анимации в этом случае достаточно исполнить команды:

> wave3 := wave(10,1,1):

> display(wave3,insequence=true,scaling=constrained, axes=none);

В данном случае картина распространения звуковых волн представлена на рис. 11.58. Видно, что перед источником звука происходит наслоение фронтов волн — создается так называемый звуковой барьер.

Рис. 11.58. Картина звуковых волн от источника звука, перемещаемого со скоростью звука

Если источник звука движется со скоростью, превышающей скорость звука, то для имитации этого эффекта надо задать команды:

> wave4 := wave(10,1.5,1.5):

> display(wave4, msequence=true, sealirtg=constrained, axes=none);

В этом случае (рис. 11.59) волны звука как бы отрываются от источника и образуют в пространстве характерный конус с вершиной в области источника звука.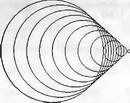

Рис. 11.59. Картина звуковых волн от источника звука, перемещаемого со скоростью, превышающей скорость звука

Наблюдаемый конус называют конусом Маха. Угол раствора конуса α определяется из выражения sin(α/2)=c/v= 1/M, где M=v/c — число Маха.

Наконец, рассмотрим случай, когда источник звука движется с переменной скоростью (с ускорением), преодолевает звуковой барьер и в конце имитации движется со скоростью выше скорости звука. Для создания такой имитации можно использовать команды:

>wave5 := wave(10,0.5,2.5):

>display(wave5, insequence=true, scaling=constrained, axes=none);

Картина звуковых волн для этого случая представлена на рис. 11.60. Здесь можно отчетливо наблюдать переход от случая движения источника звука с малой скоростью к случаю движения с большой скоростью, превышающей скорость звука. При этом видно возникновение и преодоление звукового барьера, на практике сопровождаемое громким хлопком, напоминающим взрыв.

Рис. 11.60. Картина звуковых волн от источника звука, перемещаемого с переменной скоростью, в конце превышающей скорость звука

В приведенных примерах мы ограничивались показом завершающего кадра анимации. Но читатель может просмотреть все кадры, обратившись к уже описанным средствам анимации, например из меню правой клавиши мыши (показано справа от рисунка на рис. 11.60).