|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Глава 3Работа с математическими выражениями и функциями Центральным понятием математики являются математические выражения, которые представляют собой конструкции, созданные с помощью констант, переменных, операторов и функций. В этой главе описана практика работы с выражениями, вычисляемыми с помощью встроенных в Maple 9.5/10 операторов и функций — как элементарных, так и специальных. 3.1. Работа с операторами3.1.1. Операторы и операндыОператоры являются специальными знаками, которые используются в записях математических выражений для указания того, какие виды операций должны в них выполняться. Наиболее распространенными, и одинаковыми во всех системах компьютерной математики, являются арифметические операторы + (сложения), — (вычитания), * (умножения), / (деления) и возведения в степень ^. К операторам относятся круглые ( ), квадратные [ ] и фигурные {} скобки, разделительная точка, запятая, двоеточие, точка с запятой и др. Операторы применяются совместно с данными, которые они используют и которые именуются операндами. Операнды, используемые совместно с операторами, могут быть числами, константами, переменными и математическими выражениями. К примеру, в выражении (2+3)+5 операторами являются знаки + и скобки ( ), а операндами — константы 2 и 3 для первого оператора сложения и выражение (2 + 3) и константа 5 для второго оператора сложения. Аналогично в выражении (а+b)–с операндами будут переменные a, b и с. Следует отметить, что в математических выражениях операторы имеют общепринятый приоритет, то есть порядок выполнения операторов в сложном выражении. Низшим приоритетом обладают операторы сложения и вычитания. Более высокий приоритет у операторов умножения, деления, затем возведения в степень, выполнения логических операций и так далее. Для изменения приоритета операций в математических выражениях используются круглые скобки. Выражения в скобках выполняются в первую очередь вне зависимости от приоритета входящих в них операций. Степень вложения скобок во всех современных математических системах не ограничивается. Понятие приоритета облегчает однозначную интерпретацию математических выражений. К примеру, в выражении 2+3*5 вначале будет вычислено 3*5, а затем к результату прибавится 2. В итоге будет вычислено значение 17. А в выражении (2+3)*5 вначале будет вычислено выражение в скобках (2+3), затем оно будет умножено на 5, так что результат будет 25. Таким образом скобки позволяют менять приоритет операций. Степень вложения скобок в современных системах компьютерной математики не ограничена. Однако иногда применение лишних скобок может повлиять на выбор правил вычисления выражений, например при вычислении степеней. 3.1.2. Виды операторовФормально операторы представлены своими идентификаторами в виде специальных математических знаков, слов и иных имен. Операторы, как это вытекает из их названия, обеспечивают определенные операции над данными, представленными операндами. Имеется пять основных типов операторов: • binary — бинарные операторы (двумя операндами); • unary — унарные операторы (с одним операндом); • nullary — нуль-арные операторы (без операнда — это одна, две и три пары кавычек); • precedence — операторы старшинства (включая логические операторы); • functional — функциональные операторы. Для просмотра операторов и их свойств можно использовать следующие команды вида: > ?operators[вид]; где вид — название вида оператора, указанное выше. Будет выведена страница справки по операторам заданного вида. А для изучения примеров применения операторов нужно задать и исполнить команду > ?operators[examples]; Команда > ?define; позволяет ознакомиться с функций define. С ее помощью можно определять новые операторы. 3.1.3. Применение бинарных (инфиксных) операторовБинарные операторы, именуемые также инфиксными, используются с двумя операндами, обычно размещаемыми по обе стороны от оператора. В ядро Maple включено около трех десятков бинарных операторов. Основные из них перечислены в таблице 3.1. Чуть позже мы рассмотрим и другие бинарные операторы. Примеры вычисления выражений с бинарными операторами (файл ор): > 2+3-(-4);9 > [2^3,2**3];[8,8] > 7 mod 5;2 > [3@2,3@@2];[3, 3(2)] > [х@х,х@@х];[x(2), x(x)] > [х$3,х$4];[х, x, x, x, x, x, x] Таблица 3.1. Бинарные операторы
> int(х^2,х=1..4);21 > S: = `Hello` || ` my ` || `friend!`;S := Hello my friend! Оператор композиции @@ может использоваться для создания и вычисления сложных функций, содержащих цепные дроби: > f:=а->1/(1+а);(f@@3)(а); 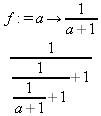 > f(5); 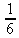 > g:=а->1/(1+а^2);(g@@3)(а); 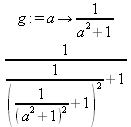 > g(2); 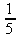 А вот еще один пример применения этого оператора для составления цепного радикала и вычисления ряда таких цепочек в цикле: > f := х -> sqrt(1 + х); 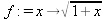 > f(f(0));√2 > f(f(f(0))); 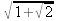 > (f@@10)(x); 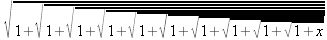 > for k from 1 to 10 do (f@@k)(0) = evalf((f@@k)(0)); od; 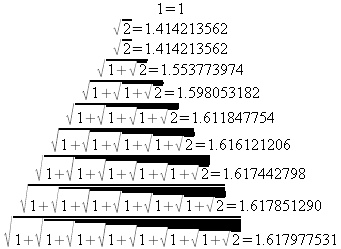 3.1.4. Работа с множествамиМножества, относящиеся к первичным понятиям, не являются точно определенными математическими объектами. Можно рассматривать, например, различные множества чисел, множества людей или деревьев и т.д. Будем считать, что они определяют группу неповторяющихся объектов. Для работы с множествами определены следующие бинарные операторы: • union — включает первый операнд (множество) во второй; • intersect — создает множество, содержащее общие для операндов элементы; • minus — исключает из первого операнда элементы второго операнда. В любом случае в результирующем множестве устраняются повторяющиеся элементы. Примеры вычисления выражений с этими операторами приведены ниже (файл sets): > {a,a,b,с,с,d} union {e,e,f,g};{f,g,a,b,e,с,d} > {a,a,b,с,с,d} intersect {a,c,e,e,f,g};{a, c} > {a,a,b,c,c,d} minus {a,d};{b, c} Напоминаем, что эти операторы заданы ключевыми словами. Несмотря на фундаментальность понятия множества, множества применяются в конкретных расчетах довольно редко. 3.1.5. Новый оператор in в множествахНачиная с Maple 8 для удобства работы с множествами был добавлен новый оператор in. Он может использоваться в виде (файл sets): element in objs или element in SetOf(type) где element — элемент множества или списка objs, type — тип выражения. Применение оператора in поясняет несколько примеров: > a in {а, b, с, d};а ∈ {b, а, с, d} > evalb(%);true > 3 in {1,2,3} intersect ({1,2,6} minus {1,4,7});3 ∈ {2} > evalb(%);false > evalb(1 in '{1,2,3} intersect ({1,2,6} minus {1,4,7})');false > is( у in SetOf( real ) ) assuming x :: fraction;false > is( x in SetOf( real ) ) assuming x :: fraction;true > coulditbe( x in SetOf ( integer ) ) assuming x ::rational;true 3.1.6. Применение унарных арифметических операторовУнарные операторы используются с одним операндом. Они могут быть префиксными, если оператор стоит перед операндом, и постфиксными, если он стоит после операнда. К унарным относятся семь операторов, приведенных в табл. 3.2. Таблица 3.2. Унарные операторы
Примеры применения унарных операторов в Maple 9.5: > [-x,x+(-x),х+(+х)];[-x, 0, 2х] > 20!;2432902008176640000 > .234;.234 > 2.34;2.34 > 2*%;4.68 > а$3;а, a, а 3.1.7. Применение оператора % и команды historyМы уже неоднократно отмечали, что в Maple оператор % обеспечивает подстановку в строку ввода (или в выражение) последнего результата операции, %% — предпоследнего и %%% — третьего с конца. Есть еще одна иногда полезная возможность проследить за ходом частных вычислений внутри документа — применение команды-функции history. Функция history(expr) или history() создает список переменных вида Oi, где индекс i=1, 2, 3… . Этим переменным можно присваивать значения в диалоговом режиме и отслеживать результаты вычислений. Команда off;, вводимая после использования данной функции, завершает работу с ней. Ниже представлен диалог с применением функции history: > history(); O1 := 2;2 O2 := sin(1.);.8414709848 O3 := O1*O2; 1.682941970 O4 := off; > %;history К сожалению, полученный результат и значения глобальных переменных Oi после завершения работы с данной функцией становятся недоступными, так что практической пользы от ее применения не так уж много. Разумеется, внутри блока history вы можете присвоить результат другой переменной, и он сохранится. При каждом очередном применении функции history нумерация переменных Oi начинается с начала, так что какой-либо преемственности при использовании этой функции нет. Функция history может применяться в качестве средства начальной отладки вычислений. Внутри фрагмента программы, заданного функцией history, можно задавать построения графиков. Например, при исполнении фрагмента программы > history(); O1 := sin(х);sin(x) O2 := plot(O1,х=0..20) ; O3:= off; будет построен график синусоиды. В целом работа с функцией history отличается не слишком высокой стабильностью, так что возможности этой функции пока остаются не слишком востребованными. 3.1.8. Работа с логическими операторамиЛогические операторы, именуемые также булевыми, указывают на логическую связь величин (или выражений). Они представлены рядом бинарных операторов, приведенных в табл. 6.3 и реализованы во всех СКМ. Таблица 3.3. Бинарные логические операторы
Конструкции с этими операторами, такие как х=у, возвращают логическое значение — константу true, если условие выполняется, и false, если оно не выполняется. Кроме того, к логическим операторам относится унарный оператор not — он представляет логическое «нет». Для возврата логических значений выражений с этими операторами в Maple 9.5 используется функция evalb(условие), например (файл evalb): > 5<2 ;5 < 2 > evalb(%);false > evalb(4=2+2);true > evalb(3<>3);false > evalb(not(%));true > evalb(3=3 and 4>2);true > evalb(3=3 or 2<0);true > evalb(x*y=y*x);true Логические операторы часто используются в управляющих структурах программ, составленных на языке программирования Maple. Такое их применение мы рассмотрим позже. 3.1.9. Применение операторов специальных типовОператоры в Maple описывают операции по преобразованию данных, в частности, выражений. Последние, в свою очередь, можно отнести к данным абстрактного типа. Могут быть описаны следующие типы операторов: • неопределенные (f); • нейтральные (&); • процедурные; • функциональные; • композиционные (@). Оператор относится к неопределенным, если он не был заранее определен. Такой оператор не выполняет никаких действий и просто повторяется в строке вывода: > restart:f(1,2,а); f(1, 2, а)Композиционные операторы (на базе знака @) мы уже применяли. Другие типы операторов рассмотрены ниже. 3.1.10. Применение функциональных операторовФункциональные операторы Maple-языка являются альтернативами функций и записываются в двух формах.
Данные операторы могут использоваться для реализации подстановок. Например, запись х->х^2 означает подстановку х^2 на место переменной х. Возможны и такие подстановки в множественной форме: (х,у) -> x^2 + у^2 х -> (2*х, 3*х^4) (х,у,z) -> (х*у, y*z) Функциональный оператор в Maple часто используется для задания функций пользователя, которое будет рассмотрено несколько позднее. 3.1.11. Определение нейтральных операторовДля создания нейтральных операторов (задаваемых пользователем и в момент задания неисполняемых), определяемых пользователем, служит знак амперсанда — &. Синтаксис нейтрального оператора следующий: &name Имя оператора строится по правилам задания допустимых идентификаторов. Также в качестве имени может быть использована последовательность (один и более) специальных символов. В последовательности специальных символов не должно быть букв, цифр, подчеркивания, а также следующих символов: & | (){}[]:;'` # <перевод строки> <пробел> Максимальная длина имени — 495 символов. Нейтральные операторы могут быть унарными и бинарными. Примеры задания бинарного нейтрального оператора приведены ниже: > х&/у;x&/y > z+x&/y;z+(x&/y) > &/(х, у);x &/ у > х&/у-&/(х,у);0 3.1.12. Определение операторов с помощью оператора defineБольшие возможности для создания операторов с заданными свойствами предоставляет специальный оператор define. Он записывается в следующей форме: define(oper, property1, property2, ...) Здесь oper — имя определяемого оператора, property1, property2 и т.д. — наименования свойств. В принципе оператор define позволяет создавать операторы с новыми свойствами, которые отсутствуют у операторов и функций, встроенных в систему. Могут быть указаны следующие свойства операторов: unary — унарный оператор; binary — бинарный оператор; diff — дифференциальный оператор; linear — линейный оператор; multilinear — множественный линейный оператор; flat — ассоциативный оператор, для которого f(х,f(y,z)) = f(f(х, y), z) =f(х, у, z); orderless — коммутативный симметричный оператор, такой что f(х, y) = f(y, х); antisymmetric — асимметричный оператор, такой что f(х, y) = -f(у, х); zero — нулевой оператор (например, V:=Vector(5,shape=zero) задает вектор с 5 нулевыми элементами); identity — единичный оператор (например, M:=Matrix(3,3,shape=identity) задает единичную матрицу). Следующий пример задает линейный оператор L: > define(L,linear); > L(а*х+b*х^2+с*х^3);L(ax) + L(bx²) + L(cz³) Для задания некоторых свойств операторов можно использовать уравнения и соотношения вида f(x)=value. Чтобы свойство выполнялось для всех аргументов (или некоторого класса аргументов), используется описание forall. Так, приведенный ниже пример задает оператор F, который вычисляет n-е число Фибоначчи (n>2): > restart; > define(fib,fib(0)=1,fib(1)=1,fib(n::posint)=fib(n-1)+fib(n-2)); > fib(6);13 > fib(10);89 > fib(20);10946 Обратите внимание на то, что соотношения fib(0)=1 и fib(1)=1 задают начальные значения целочисленного массива чисел Фибоначчи, которые нужны для реализации обычного итерационного алгоритма их нахождения — напоминаем, что очередное число Фибоначчи равно сумме двух предшествующий чисел Фибоначчи. 3.2. Работа с математическими функциями3.2.1. Понятие о функцияхБолее двух сотен лет тому назад в обиход математиков пришло понятие функции, как некоторой зависимости одной величины, например f или у, от другой величины — независимой переменной х или t. Функции стали обозначать как f(x), f(t), y(x) и т.д. Могут быть и функции ряда переменных, например вида f(х, у, z, …). Хотя эти понятия не являются полными, мы ограничимся ими, помня, однако, что функции могут быть определены в различных интервалах изменения их аргументов. В Maple функция это имеющий уникальное имя (идентификатор) объект математического выражения, выполняющий некоторое преобразование своих входных данных, представленных списком входных параметров. Суть этого преобразования соответствует некоторой функциональной зависимости возвращаемого функцией значения от входных параметров функции. Например, функция sin(x) возвращает значение, которое является синусом входного параметра х. Таким образом, признаком функции является возврат ею некоторого значения. Входные параметры изначально являются формальными и представляются именами некоторых переменных. Особенностью функции является возврат ее значения в ответ на обращение к функции по имени с указанием фактических параметров в списке параметров функций. Фактические параметры могут быть различными константами, определенными переменными и даже вычисляемыми математическими выражениями. К примеру, sin(x) является синтаксической формой записи математической функции синуса — sin(x). При этом х — формальный параметр. А уже в выражении sin(1.0) числовая константа 1.0 является фактическим параметром в виде вещественного числа, причем sin(1.0) возвращает численное значение синуса угла в 1 радиан. Функция atan2(x, y) является примером функции, имеющей список из двух формальных параметров — х и у. Как правило, в системах символьной математики принципиально важно, как записан фактический параметр. Например, число 1. или 1.0 является вещественным, на что указывает разделительная точка. Если число представлено в виде 1, то оно рассматривается как целое и константа. Большинство систем символьной математики не вычисляет выражения вида sin(1) или sin(π/2), а выводит их в исходном виде. Это связано с тем, что такой вид дает о значении функции гораздо больше информации, чем просто ее вычисленное значение. Благодаря свойству возврата значений функции применяются для построения математических выражений наряду с операторами. Например, математическое выражение 2*sin(x) содержит функцию sin(x) и оператор умножения *. Математические выражения могут быть как очень простыми (наподобие приведенного), так и очень сложными, включающими в себя операторы интегрирования, дифференцирования и иные специальные операторы и функции, а также сложную многоуровневую систему скобок. Функции обычно подразделяются на четыре типа: • встроенные в ядро системы предопределенные функции или внутренние функции; • функции пользователя; • библиотечные функции, вызываемые из пакетов или библиотек расширения системы, например sin(x) или ln(x); • функции, заданные в виде программного модуля. Кроме того, функции могут классифицироваться по характеру производимых ими преобразований входных параметров. Они делятся на алгебраические, тригонометрические, обратные тригонометрические, гиперболические, обратные гиперболические, специальные и так далее. В математических системах Maple функции могут применяться со специальными директивами и опциями. Они могут задаваться как дополнительный параметр функции. 3.2.2. Математические выраженияМатематические выражения это сложные (комбинированные) объекты, которые состоят из операторов, операндов и функций со списками их параметров. Например, в выражении (2+3)*sin(x) скобки ( ) и знаки + и * являются операторами, константы 2 и 3 — операндами, sin(x) — встроенной функцией, а х — входным параметром функции. Для оператора умножения выражение (2+3) и функция sin(x), т.е. по существу тоже выражение, являются операторами. Приоритет функций более высокий, чем у операторов. В системах для численных расчетов математические выражения применяются в естественном виде и в разборе их структуры нет особой необходимости. Исключение составляет разве что анализ скобок, меняющих приоритет выполнения операций в выражениях. Иное дела системы символьной математики. У них в ходе вычислений выражения эволюционируют, то есть видоизменяются по мере выполнения расчетов. Это может приводить к весьма неожиданным последствиям, например, когда сложнейшее выражение упрощается к 0 или 1, а внешне совсем не страшное выражение разворачивается так, что не помещается в десятке страниц экрана. Набор средств по разбору структуры и преобразованиям математических выражений в таких системах настолько велик, что всерьез разобраться с ними под силу математику-аналитику или достаточно опытному пользователю. Поэтому мы оставим рассмотрение функций анализа выражений на потом — оно будет дано при описании средств символьной математики. 3.2.3. Работа с элементарными функциями в системе MapleMaple имеет полный набор элементарных математических функций [38–41]. Все они, кроме арктангенса двух аргументов, имеют один аргумент х, например sin(x). Он может быть целым, рациональным, дробно-рациональным, вещественным или комплексным числом. В ответ на обращение к ним элементарные функции возвращают соответствующее значение. Поэтому они могут быть включены в математические выражения. Все описанные здесь функции называются встроенными, поскольку они реализованы в ядре системы. Как правило, если аргументом функции является фундаментальная константа, целое или рациональное число, то функция выводится с таким аргументом без получения результата в форме действительного числа с плавающей точкой. Например (файл calcfun): > sin(Pi);0 > sin(1);sin(1) > exp(1);e > ln(2);ln(2) > ln(Pi);ln(π) > arcsin(1/2); 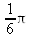 > arcsin(1/3);arcsin(⅓) Нетрудно заметить, что есть и исключения из этого правила — например, на экране монитора ехр(1) будет выведено как константа е, а значение функции arcsin(1/2) все же вычислено и результат получен как 1/6 от константы Pi. Вообще говоря, если результат выражается через фундаментальную математическую константу, то он будет вычислен и представлен ею. В противном случае функция с целочисленным и рациональным аргументом или с константой просто повторяется в строке вывода в установленном для этой строки формате. Для получения подробной информации о некоторой произвольной функции <f> достаточно задать команду > ? <f> Например, команда > ? sin открывает окно справки по тригонометрическим функциям, включая функцию синуса. Ввиду общеизвестности элементарных функций мы не будем обсуждать ни их свойства, ни допустимые для них пределы изменения аргумента. Эти вопросы отражаются в любом учебнике по элементарной математике. 3.2.4. Некоторые целочисленные функции и факториалНиже представлены наиболее распространенные целочисленные функции Maple, используемые в теории чисел: • factorial(n) — функция вычисления факториала (альтернатива — оператор !); • iquo(a,b) — целочисленное деление а на b; • irem(a,b) — остаток от деления а на b; • igcd(a,b) — наибольший общий делитель; • lcm(a,b) — наименьшее общее кратное. Факториал целого числа N задается как N= 1*2*3*...*N при особых случаях 0!=1 и 1!=1. Примеры применения функций, отмеченных выше (файл calcfun): > [factorial(10),10!];[3628800, 3628800] > iquo(234,5);46 > irem(234,5);4 > lcm(124,3);372 > [3!!, (3!)!];[720, 720] В последних двух примерах применения оператора факториала полезно обратить внимание, что запись n!! означает лишь (n!)!, а не n!! = 2*4*6*…, то есть произведение четных целых чисел. Действие других функций очевидно. Целочисленные функции, хотя и не все, не могут использоваться для символьных операций, например интегрирования или дифференцирования. Полезность возможности Maple вычислять факториалы больших чисел демонстрирует следующий пример. Пусть в группе студентов 25 человек, а в году 365 дней. Тогда вероятность того, что ни у кого из студентов дни рождения не совпадают, составит: 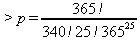 > evalf(%);р = 0.2780571566 10-25 При обычной арифметике был бы получен 0 или сообщение о некорректности операций из за превышения разрядной сетки компьютера. А вот еще более характерный пример такого рода. Пусть вероятность рождения мальчика 0.515. Какова вероятность того, что среди 1000 новорожденных мальчиков будет не менее половины. Расчетная формула требует вычисления факториала 1000!: 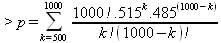 > evalf(%);р = 0.8366435978 Если увеличить число рождаемых мальчиков до 10 или 100 тысяч, то такая задача может послужить хорошим тестом не только на работу с очень большими числами, но и на скорость вычислений. Решение таких задач без применения аппарата точной арифметики больших чисел встречает большие трудности, а подчас и просто невозможна. 3.2.5. Функции с элементами сравнения и их применениеНесколько хорошо известных функций использует при вычислениях средства сравнения чисел. Для действительного аргумента х это следующие функции: • trunc(x) — при х>=0 возвращает наибольшее целое, меньшее или равное х, при x<0, trunc(x) = -trunc(-x). • round(x) — округляет x до ближайшего целого. • frac(x) — возвращает дробную часть х, так что frac(x) = х - trunc(x). • floor(x) — возвращает наибольшее целое, меньшее или равное х. • ceil(x) — возвращает наименьшее целое, большее или равное х. Эти функции могут использоваться и для комплексного аргумента х. При этом справедливы следующие соотношения: trunc(x) = trunc(Re(x)) + I*trunc(Im(x)) round(x) = round(Re(x)) + I*round(Im(x)) frac(x) = frac(Re(x)) + I*frac(Im(x)) ceil(x) = -floor(-x) К этой категории относится и функция знака, синтаксис которой: signum(x) signum(1,x) signum(0, х, у) В основной (первой) форме она возвращает значение x/abs(x), где функция abs(x) — возвращает абсолютное значение действительного х, т.е. х при х>0 и -х при х<0. Действия, выполняемые этими функциями, вполне очевидны и читатель может легко проверить это на практике. Данные функции можно использовать для моделирования периодически повторяющихся зависимостей (сигналов). Несколько таких примеров представлено ниже (файл modsig — рис. 3.1): > restart; RC:=2-2*ехр(3*(floor(t/2)-t/2)); upside:=1/(3+2*sin(Pi*t)); sawtooth:=t-floor(t): roundsquare: = (tanh(100*sin(Pi*t) )+1) /2: squarewave:= (1+signum(sin (Pi*t)))/2; blimps:=squarewave*sawtooth; triang:=blimps+(squarewave-1)*(sawtooth-1); plot([sawtooth+5, upside+3, RC,blimps-2,squarewave-4,roundsquare-6,triang-8],t=0..10,-8..6, color=[red,orange,green,black,magenta,brown,blue], thickness=3); 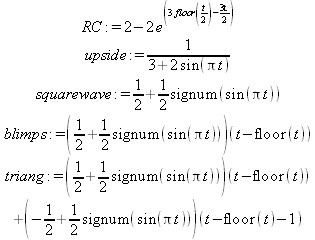 Графики зависимостей, получаемые с помощью представленного выше примера показаны на рис. 3.1. Эти зависимости можно использовать в качестве моделей сигналов при моделировании электрических и электронных цепей (см. главу 11).  Рис. 3.1. Графики зависимостей, получаемых с помощью функций сравнения 3.2.6. Примеры вычисления тригонометрических функцийВ ядре Maple (и других СКМ) определены следующие тригонометрические функции: sin — синус; cos — косинус; tan — тангенс; sec — секанс; csc — косеканс; cot — котангенс. Все эти функции являются периодическими (с периодом 2π, кроме тангенса и котангенса, у которых период равен π) и определены для действительного и комплексного аргументов. Примеры вычислений (файл calcfun): > [sin(1), sin(1.)];[sin(1), .8414709848] > sin(x)^2+cos(x)^2;sin(x)² +cos(x)² > simplify(%);1 > simplify(tan(x)*cos(x));sin(x) > sec(2+3*1);sec(2 + 3I) > sec(2.+3*I);-.04167496441 + .09061113720 I > cot(I);-I coth(1) > csc(I);-I csch(1) Многие свойства тригонометрических функций можно оценить, рассматривая их графики. Для построения таких графиков средствами Maple можно использовать функцию plot. Примеры построения графиков тригонометрических функций даны в файле tfris. 3.2.7. Гармонический синтез пилообразных колебанийФундаментальная роль функций синуса и косинуса проявляется в решении задач спектрального анализа и синтеза. В Maple они реализуются с помощью функций прямого и обратного преобразований Фурье [39, 43]. Однако, смысл гармонического синтеза проще всего понять, просто суммируя синусоидальные функции с кратной частотой — гармоники. При этом характер результирующего колебания зависит от того, какие гармоники берутся (все, только четные или только нечетные), а также от того, по какому закону меняется амплитуда колебаний и их фаза в зависимости от номера гармоники. Покажем это на паре примеров. На рис. 3.2 показан пример гармонического синтеза двух периодов пилообразного колебания (сигнала) при суммировании 3, 10 и 60 гармоник. Отчетливо видно, что по мере увеличения числа гармоник форма колебаний действительно приближается к треугольной. В условиях резкого ограничения числа гармоник в местах предполагаемого разрыва колебаний наблюдаются характерные колебания — эффект Гиббса.  Рис. 3.2. Гармонический синтез треугольных колебаний по 3, 10 и 60 гармоникам Колебания описанной формы получаются за счет синтеза всех гармоник, причем амплитуда гармоник равна 1/k, где k — номер гармоники. 3.2.8. Гармонический синтез меандраА теперь рассмотрим синтез симметричных прямоугольных колебаний, получивших название — меандр. Для синтеза меандра надо использовать только нечетные гармоники, т. е. с номерами n=1, 3, 5, … Проще всего получить нечетные числа, используя вместо параметра n значение 2n–1. Тогда для получения 3, 9 и 59 нечетных гармоник надо будет использовать значения n до 2, 5 и 30. Рис. 3.3 иллюстрирует синтез меандра. 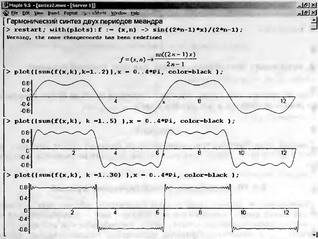 Рис. 3.3. Гармонический синтез меандра при n = 2, 5 и 30 Читатель, интересующийся вопросами гармонического синтеза сигналов может опробовать в нем свои силы и синтезировать колебания и сигналы других форм. Поскольку при синтезе сигнал получается в виде частотных составляющих (гармоник), то для преобразования такого сигнала можно использовать частотные фильтры. 3.2.9. Обратные тригонометрические функции и их применениеК обратным тригонометрическим функциям относятся: arcsin — арксинус; arccos — арккосинус; arctan — арктангенс; arcsec — арксеканс; arccsc — арккосеканс; arccot — арккотангенс. Примеры вычислений (файл calcfun): > arcsin(.2);.2013579208 > arcsin(2.);1.570796327 - 1.316957897 I > evalc(arcsin(5));½π - I ln(5+2√6) > arccos(1/2);⅓π > arctan(1);¼π > arccot(0);½π К этому классу функций принадлежит еще одна полезная функция: arctan(y,x) = argument(х+I*у) Она возвращает угол радиус-вектора в интервале от -Pi до Pi при координатах конца радиус-вектора х и у (см. пример ниже): > arctan(2., 3);.5880026035 Графики ряда обратных тригонометрических функций строит документ, имеющийся в файле tfris. Следует отметить, что эти функции не являются периодическими. 3.2.10. Применение гиперболических функцийГиперболические функции представлены следующим набором: sinh — гиперболический синус; cosh — гиперболический косинус; tanh — гиперболический тангенс; sech — гиперболический секанс; csch — гиперболический косеканс; coth — гиперболический котангенс. Примеры применения гиперболических функций представлены ниже (файл calcfun): > [sinh(1.), cosh(1.), tanh(1.)];[1.175201194, 1.543080635, .7615941560] > [sech(1.), csch(1.), coth(1.)];[6480542737, .8509181282, 1.313035286] На рис. 3.4 сверху представлены графики гиперболического синуса, косинуса и тангенса. По ним можно судить о поведении этих функций. 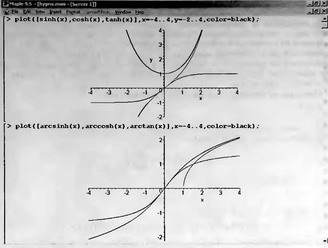 Рис. 3.4. Графики основных гиперболических и обратных гиперболических функций В отличие от тригонометрических функций, гиперболические функции не являются периодическими. Функция гиперболического тангенса имеет симметричную кривую с характерными ограничениями. Поэтому она широко используется для моделирования передаточных характеристик нелинейных систем с ограничением выходного параметра при больших значениях входного параметра. С помощью функции преобразования convert(f, ехр) можно перевести гиперболические функции в экспоненциальную форму: > convert(sinh(х),ехр); 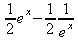 > convert(tan(х),ехр); 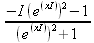 3.2.11. Обратные гиперболические функции и их применениеК обратным гиперболическим функциям относятся: arcsinh — гиперболический арксинус; arccosh — гиперболический арккосинус; arctanh — гиперболический арктангенс; arcsech — гиперболический арксеканс: arccsch — гиперболический арккосеканс: arccoth — гиперболический арккотангенс. Примеры применения: > [arcsinh(1.),arccosh(1.), arctanh(1.)];[.8813735870, 0., Float(∞) + Float(undefined)I] Графики обратных гиперболических синуса, косинуса и тангенса представлены на рис. 3.4 снизу. С помощью функции преобразования convert(f, ln) можно перевести гиперболические функции в логарифмическую форму: > сonvert(arcsin(х), ln); 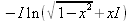 > convert(arctan(х), ln); 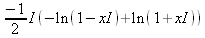 3.2.12. Вычисление степенных и логарифмических функцийК степенным и логарифмическим относятся следующие функции системы Maple: ехр — экспоненциальная функция; ilog10 — целочисленный логарифм по основанию 10 (возвращает целую часть от логарифма по основанию 10); ilog — целочисленный логарифм (библиотечная функция, возвращающая целую часть от натурального логарифма); ln — натуральный логарифм; log — логарифм по заданному основанию (библиотечная функция); log10 — логарифм по основанию 10; sqrt — квадратный корень. Примеры вычисления этих функций (файл calcfim): > х:=2;х:=2 > [ехр(х),ln(х),log(х),log10(х)]; 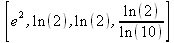 > х:=2.0;х:= 2.0 > [ехр(х),ln(х),log(х),log10(х)];[7.389056099,.6931471806,.6931471806,.3010299957] > ilog[2](100);6 > readlib(log10);proc(x) ... end proc > log10(10000.);4.000000000 > evalc(sqrt(2+3*I)); 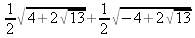 > sqrt(99+1);13 Графики ряда описанных выше функций показаны на рис. 3.5. Они также получены с применением средств Maple 9.5. 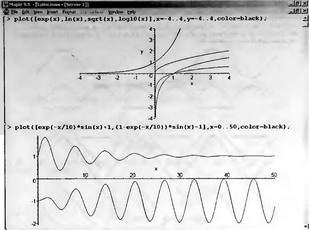 Рис. 3.5. Графики ряда степенных и логарифмических функций На рис. 3.5 показаны также графики синусоиды с экспоненциально падающей и нарастающей амплитудой. Строго говоря, называть представленные функции синусоидами математически не корректно. Многие функции этой группы обычно определены для положительных значений аргумента. Однако введение комплексных чисел позволяет вычислять такие функции и для отрицательных значений аргумента. Несколько интересных примеров этого представлено ниже (файл calcfun): > restart:sqrt(-4);2I > simplify( sqrt(х^2));csgn(x)x > ln( -1 );πI > simplify(log(exp(x)));ln(ex) > assume(x,positive);simplify(log(exp(x)));x~ Обратите внимание на то, что в предпоследнем примере Maple отказалась вычислить «очевидное» значение выражения, но сделала это после придания х статуса предполагаемой переменной с только положительными значения. 3.2.13. Применение элементарных функция для моделирования сигналовСистемы компьютерной математики часто используются для моделирования сигналов и устройств их обработки и преобразования (см. пример в разделе 3.2.5). Рисунок 3.6 показывает построение нескольких функций, полученных с помощью комбинаций элементарных функций, включая тригонометрические функции. Такие комбинации позволяют получать периодические функции, моделирующие сигналы стандартного вида: в виде напряжения на выходе двухполупериодного выпрямителя, симметричных прямоугольных колебаний (меандр), пилообразных и треугольных импульсов, треугольных импульсов со скругленной вершиной. 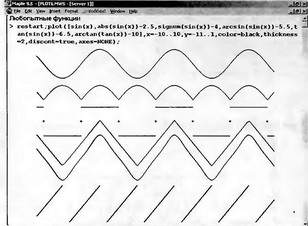 Рис. 3.6. Примеры моделирования сигналов с помощью комбинаций элементарных функций В этом рисунке запись axes=NONE убирает координатные оси. Обратите внимание, что смещение графиков отдельных функций вниз с целью устранения их наложения достигнуто просто прибавлением к значению каждой функции некоторой константы. Приведенные выше сигналы нередко можно формировать, используя функции с условиями — например, функцию signum. Однако достоинство моделирования сигналов с помощью только элементарных функций заключается в том, что такие сигналы нередко могут обрабатываться аналитически, тогда как для функций с условиями это возможно далеко не всегда. 3.2.14. Выбор экспоненциальных функций для приближения сложных зависимостейВ природе многие зависимости имеют экспоненциальное нарастание или спад. Это характерно для апериодических и релаксационных процессов, например, таких как спад радиоактивности. Да и многие колебательные процессы имеют экспоненциальное нарастание или спад амплитуды колебаний. Кроме того, такие зависимости характерны для ряда характеристик самых разнообразных устройств и систем. Это делает целесообразным рассмотрение и визуализацию наиболее важных из экспоненциальных функций. На рис. 3.7 показано начало документа на котором заданы три экспоненциальные функции и построены семейства их графиков. Представление графиков в виде семейства, а не поодиночке, позволяет наглядно представить характер изменения вида функций, что зачастую уже достаточно для выбора той или иной функции в качестве приближения (аппроксимации) некоторой сложной зависимости. После выбора зависимости используя методы регрессионного анализа можно подобрать параметры выбранной функции по методу наименьших квадратов. 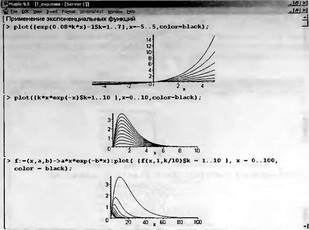 Рис. 3.7. Начало документа с тремя экспоненциальными зависимостями Первая из представленных функций описывает зависимости, характерные для идеального диода или р-n-перехода. Две другие зависимости имеют характерные падающие участки, которые присуши, например, вольт-амперным характеристикам «лямбда»-диодов и транзисторов (первые характеризуются одной кривой, другие семейством кривых). Последняя зависимость задана функцией пользователя с тремя параметрами x, а и b. Еще три зависимости, представленные на рис. 3.8 также весьма напоминают характерные для ряда систем и устройств характеристики. Первая зависимость очень похожа на нормированные резонансные кривые колебательных контуров и иных резонаторов. Другая зависимость позволяет моделировать нелинейные характеристики усилителей. Ее замечательные свойства — симметрия и возможность изменения плавности перехода от одного состояния (0) к другому (1). А третья зависимость характеризует сдвиг по горизонтали некоторой передаточной зависимости. Она также очень напоминает кривые гистерезиса магнитных материалов. 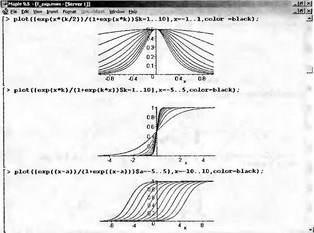 Рис. 3.8. Часть документа с тремя дополнительными экспоненциальными зависимостями Следующая тройка зависимостей представлена на рис. 3.9. Эти зависимости напоминают ранее описанные, но с некоторыми индивидуальными особенностями. Например, средняя зависимость дает спад, а не нарастание значения «выхода» при нарастании значения переменной х. Семейство зависимостей в конце рис 3.9 характерно плавным переходом от симметричной зависимости к явно несимметричной, имеющей быстрое нарастание и относительно медленный спад. Такой характер нередко имеет выходной сигнал усилителя, возбуждаемого перепадом напряжения. 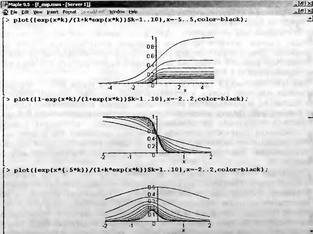 Рис. 3.9. Часть документа с еще тремя экспоненциальными зависимостями Три последние зависимости (рис. 3.10) прекрасно подходят для описания вольт-амперных характеристик ряда электронных приборов. Первые две из них напоминают семейства вольт-амперных характеристики полевых транзисторов и электронных ламп. Верхняя соответствует приборам с постоянной крутизной, на что указывает равное расстояние между кривыми. А вторая напоминает семейство вольт-амперных характеристик полевого транзистора с нарастающей при больших токах крутизной. 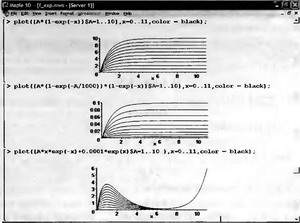 Рис. 3.10. Конец документа с началом на рис. 3.7 Последняя зависимость неплохо подходит для приближения N-образной вольт-амперной характеристики туннельного диода. Это довольно старый, но хорошо известный прибор, который применяется в усилителях и генераторах высокочастотных и сверхвысокочастотных колебаний. 3.2.15. Применение функций с элементами сравненияВ алгоритме вычисления ряда функций заложено сравнение результата с некоторым опорным значением. К таким функциям с элементами сравнения относятся: abs — абсолютное значение числа; ceil — наименьшее целое, большее или равное аргументу; floor — наибольшее целое, меньшее или равное аргументу; frac — дробная часть числа; trunc — целое, округленное в направлении нуля; round — округленное значение числа; signum(х) — знак х (-1 при х<0, 0 при х=0 и +1 при х>0). Для комплексного аргумента х эти функции определяются следующим образом: • trunc(x) = trunc(Re(x)) + rtrunc(Im(x)); • round(x) = round(Re(x)) + I*round(Im(x)); • frac(x) = frac(Re(x)) + I*frac(Im(x)). Для введения определения значения floor(x) от комплексного аргумента прежде всего запишем а=Re(x)-floor(Re(x)) и b=Im(x)-floor(Im(x)). Тогда floor(x)=floor(Re(x))+I*floor(Im(x))+X, где 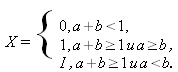 Наконец, функция ceil для комплексного аргумента определяется следующим образом: ceil(x) = -floor(-х) Примеры вычисления выражений с данными функциями представлены ниже (файл calcfun): > [ceil(Pi), trunc(Pi), floor(Pi), frac(Pi), round(Pi)];[4, 3, 3, π, -3, 3] > frac(evalf(Pi));.141592654 > [ceil(-Pi),trunc(-Pi),floor(-Pi),round(-Pi)];[-3, -3, -4, -3] > trunc(2.6+3.4*I);2+3I > [signum(-Pi),signum(0),signum(Pi)];[-1,0,1] Хотя функции этой группы достаточно просты, их нельзя относить к числу элементарных функций. Нередко их применение исключает возможность проведения символьных преобразований или дает их существенное усложнение. 3.2.16. Работа с функциями комплексного аргументаДля комплексных чисел и данных, помимо упомянутых в предшествующем разделе, определен следующий ряд базовых функций: argument — аргумент комплексного числа; conjugate — комплексно-сопряженное число; Im — мнимая часть комплексного числа; Re — действительная часть комплексного числа; polar — полярное представление комплексного числа (библиотечная функция). Примеры вычисления для этих функций (файл calcfun): > z:=2+3*I;Z:=2 + 3I > [Re(z),Im(z),abs(z)]; 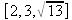 > [argument(z),conjugate(z)]; 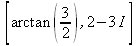 > readlib(polar);proc(r::algebraic, th::algebraic) ... end proc > polar(z); 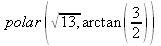 > polar(-3.,Pi/2); 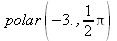 В некоторых случаях полезна визуализация операций с комплексными числами. Для этого удобен пакет расширения plots, который позволяет представлять комплексные числа в виде стрелок на комплексной плоскости. Например, для иллюстрации операции умножения двух комплексных чисел 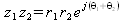 можно использовать следующие графические построения (файл complpot): > with(plottools): l1 := arrow([0,0], [1,2], .1, .3, .1, color=green): l1a := arc([0,0],1.5,0..arctan(2),color=green): > l2 := arrow([0,0], [1,-8], .1, .3, .1, color=green): l2a := arc([0,0],.75,0..arctan(.8),color=green): > l3 := arrow([0,0], [-.6,2.8], .1, .3, .1, color=black): l3a := arc([0,0],2.5,0..arctan(2.8,-.6),color=black): > plots[display](l1,l2,l3,l1a,l2a,l3a, axes=normal,view=[-3..3,0..3],scaling=constrained); Они создают график (рис. 3.11) наглядно иллюстрирующий операцию перемножения двух комплексных чисел, представленных своими радиус-векторами.  Рис. 3.11. Иллюстрация перемножения двух комплексных чисел 3.2.17. Построение графиков функций в Maplet-окнеПри изучении графиков элементарных функций вне особенностей системы Maple полезно Maplet-приложение, окно которого представлено на рис. 3.12. Открывается это окно исполнением команды Tools→Precalcus→Standard Functions… при работе в стандартном интерфейсе Maple 9.5. 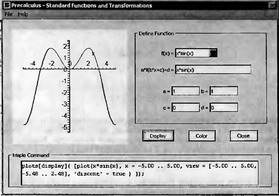 Рис. 3.12. Maplet-окно для изучения функций и построения их графиков В окне в разделе определения функций Define Function имеется список элементарных функций, графики которых можно просматривать. Однако, возможно построение и графиков простых функций более сложного вида, например x*sin(x) вместо sin(x) — это и иллюстрирует график, представленный на рис. 3.12. Maplet-окно генерирует команду на Maple-языке, которая строит график заданной функции. 3.3. Работа со специальными функциями3.3.1. Обзор специальных математических функцийСпециальные математические функции являются решениями дифференциальных уравнений, которые невозможно представить через элементарные функции. Через такие функции нередко представляются и многие интегралы. Наиболее мощные из СКМ, например Maple, широко используют специальные математические функции в ходе символьных преобразований. Рассмотрим наиболее важные специальные математические функции. Функция Эйри формирует пару линейно независимых решений дифференциального уравнения вида: 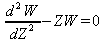 Связь между функцией Эйри и модифицированной функцией Бесселя выражается формулой: 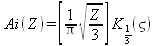 где 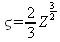 Дифференциальное уравнение вида 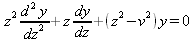 где v — неотрицательная константа, называется уравнением Бесселя, а его решения известны как функция Бесселя. J(z) и J_(z) формируют фундаментальное множество решений уравнения Бесселя для неотрицательных значений (так называемые функции Бесселя первого рода): 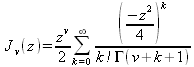 где для гамма-функции используется следующее представление: 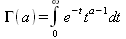 Второе решение уравнения Бесселя, линейно независимое от J(z), определяется как 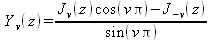 и задает функции Бесселя второго рода Y(z). Функции Бесселя третьего рода (функции Ханкеля) и функция Бесселя связаны следующим выражением: H(1)v(z) = Jv(z) + iYv(z), H(2)v(z) = Jv(z) - iYv(z). Дифференциальное уравнение вида 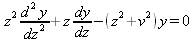 где v — неотрицательная константа — называется модифицированным уравнением Бесселя, и его решения известны как модифицированные функции Бесселя I(z) и I_(z). K(z) — второе решение модифицированного уравнения Бесселя, линейно независимое от I(z). I(z) и K(z) определяются как: 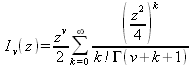 и 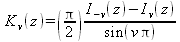 Бета-функция определяется как: 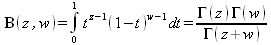 где Г(z) — гамма-функция. Неполная бета-функция определяется интегральным выражением: 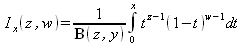 Эллиптические функции Якоби определяются интегралом: 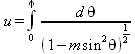 В некоторых случаях при определении эллиптических функций используются модули k вместо параметра m. Они связаны выражением: k² = m = sin² α. Полные эллиптические интегралы первого и второго рода определяются следующим образом: 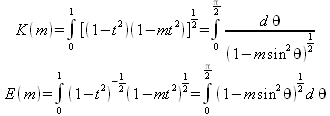 Функция ошибки (интеграл вероятности) определяется следующим образом: 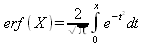 erf(X) — возвращает значение функции ошибки для каждого элемента вещественного массива X. Остаточная функция ошибки задается соотношением: 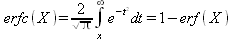 Встречается и масштабированная остаточная функция ошибки. Эта функция определяется так: eifcx(x) = еx² erfc(x)Интегральная показательная функция определяется следующим образом: 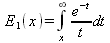 Гамма-функция определяется выражением: 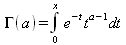 Неполная гамма-функция определяется как: 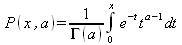 Перейдем к функциям, представляющим ортогональные полиномы. Функция Лежандра определяется следующим образом: 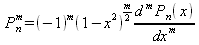 где Рn(х) — полином Лежандра степени n, определяется так: 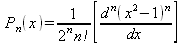 3.3.2. Специальные математические функции системы Maple 9.5Maple 9.5 имеет практически полный набор специальных математических функций: • AiryAi (Bi) — функции Эйри; • AngerJ — функция Ангера; • bernoulli — числа и полиномы Бернулли; • Bessell (J, K, Y) — функции Бесселя разного рода; • Beta — бета-функция; • binomial — биноминальные коэффициенты; • Chi — интегральный гиперболический косинус; • Сi — интегральный косинус; • csgn — комплексная сигнум-функция; • dilog — дилогарифм; • Dirac — дельта-функция Дирака; • Ei — экспоненциальный интеграл; • EllipticCE (CK, CPi, Е, F, K, Modulus, Nome, Pi) — эллиптические интегралы; • erf — функция ошибок; • erfc — дополнительная функция ошибок; • euler — числа и полиномы Эйлера; • FresneIC (f, g, S) — интегралы Френеля; • GAMMA — гамма-функция; • GaussAGM — арифметико-геометрическое среднее Гаусса; • HankelH1 (Н2) — функции Ганкеля; • harmonic — частичная сумма серии гармоник; • Heaviside — функция Хевисайда; • JacobiAM (CN, CD, CS, DN, DC, DS, NC, ND, NS, SC, SD, SN) — эллиптические функции Якоби; • JacobiTheta1 (2, 3, 4) — дзета-функции Якоби; • JacobiZeta — зет-функция Якоби; • KelvinBer (Bei, Her, Hei, Ker, Kei) — функции Кельвина; • Li — логарифмический интеграл; • InGAMMA — логарифмическая гамма-функция; • MeijerG — G-функция Мейджера; • pochhammer — символ Похгамера; • polylog — полилогарифмическая функция; • Psi — дигамма-функция; • Shi — интегральный гиперболический синус; • Si — интегральный синус; • Ssi — синусный интеграл смещения; • StruveH (L) — функции Струве; • surd — неглавная корневая функция; • LambertW — W-функция Ламберта; • WeberE — Е-функция Вебера; • WeierstrassP — Р-функция Вейерштрасса; • WeierstrassPPrime — производная Р-функции Вейерштрасса; • WeierstrassZeta — зета-функция Вейерштрасса; • WeierstrassSigma — сигма-функция Вейерштрасса; • Zeta — зета-функция Римана и Гурвица. Ввиду большого числа специальных функций и наличия множества примеров их вычисления в справочной системе Maple 9.5, ограничимся несколькими примерами вычисления наиболее распространенных специальных функций. По их подобию читатель может опробовать в работе и другие специальные функции. На рис. 3.13 даны примеры применения ряда специальных функций. Обратите особое внимание на первый пример. Он показывает, как средствами системы Maple задается определение функций Бесселя. Показано, что функции Бесселя являются решениями заданного на рис. 3.13 дифференциального уравнения второго порядка. Система Maple 9.5/10 способна вычислять производные и интегралы от специальных функций. 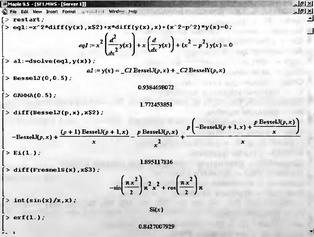 Рис. 3.13. Примеры применения специальных функций Еще несколько примеров работы со специальными функциями представлено на рис. 3.14. Как видно из приведенных примеров, на экране монитора можно получить математически ориентированное представление специальных функций, обычно более предпочтительное, чем представление на Maple-языке или в текстовом формате. Записи функций при этом выглядят как в обычной математической литературе.  Рис. 3.14. Примеры работы со специальными математическими функциями На рис. 3.14 показаны примеры разложения специальных функций в ряды и применения функции convert для их преобразования. Любопытно отметить, что в двух первых примерах рис. 3.14 вывод оказался иным, чем в предшествующих версиях Maple. Да и в них вывод для этих примеров отличался. Это говорит о непрерывной работе разработчиков над алгоритмами символьных вычислений и необходимости переработки примеров при переходе от одной версии Maple к другой. 3.3.3. Построение графиков специальных функцийМного информации о поведении специальных функций дает построение их графиков. На рис. 3.15 показано построение семейства графиков функций Бесселя BesselJ разного порядка и гамма-функции. Эти функции относятся к числу наиболее известных. Если читателя интересуют те или иные специальные функции, следует прежде всего построить и изучить их графики. 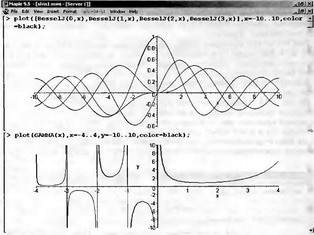 Рис. 3.15. Графики функций Бесселя и гамма-функции 3.3.4. Консультант по функциямМатематикам, серьезно работающим с функциями, большую помощь может оказать имеющийся в составе Maple 9.5 консультант по функциям, вводимый командой: FunctionAdvisor() FunctionAdvisor(topics, quiet) FunctionAdvisor(Topic, function, quiet) Здесь: topics — строковый параметр, задающий вывод тематической информации, quiet — строковый параметр, указывающий на вывод вычислительных данных, Topic — задание темы и function — задание имени функции или класса функций. Команда FunctionAdvisor() выводит правила применения консультанта по функциям (файл funcadv): > FunctionAdvisor(); The usage is as follows: > FunctionAdvisor( topic, function, ... ); where 'topic' indicates the subject on which advice is required, 'function' is the name of a Maple function, and '...' represents possible additional input depending on the 'topic' chosen. To list the possible topics: > FunctionAdvisor( topics ); A short form usage, > FunctionAdvisor(function); with just the name of the function is also available and displays a summary of information about the function. Следующие примеры показывают вывод определений функций Бесселя: > FunctionAdvisor(describe, Bessel); BesselI = Modified Bessel function of the first kind, BesselJ = Bessel function of the first kind, BesselK = Modified Bessel function of the second kind, BesselY = Bessel function of the second kind > FunctionAdvisor(describe, BesselJ); BesselJ = Bessel function of the first kind В следующем примере выводится информация о представлении функции синуса в виде ряда, представленного суммой его членов: > FunctionAdvisor(sum_form, sin); 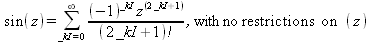 Еще один пример показывает вывод интегрального представления синусного интеграла Френеля: > FunctionAdvisor(integral form, FresnelS); 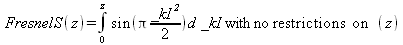 Представленные примеры дают представление лишь о малой части возможностей консультанта по функциям. С этим мощным средством получения информации о функциях можно дополнительно познакомиться по справке о нем, содержащей множество интересных примеров применения консультанта по функциям. 3.4. Работа с функциями пакетов расширения Maple3.4.1. Работа с функциями пакета комбинаторики combinatФункции комбинаторики достаточно известны из обычного курса математики. Но они применяются сравнительно редко. Поэтому они не включены в состав ядра системы, но имеются в пакете расширения combinat. При вызове пакета > with(combinat); выводится список имен его функций. Ввиду важности функций комбинаторики для некоторых специальных вычислений приведем их полные определения: • Chi(x) — гиперболический косинусный интеграл; • bell(n) — возвращает числа из решения уравнения ехр(ехр(х)-1)= sum(bell(n)/n!*x^n, n=0..infinity), причем для вычислений используется рекуррентное соотношение bell(n+1) = (bell(n)+1)^n; • binomial(n, r) — возвращает биноминальные коэффициенты, причем, если n и r — целые числа, удовлетворяющие условию 0<=r<=n, то функция возвращает C(n,r)=n!/(r!(n-r)!), а в общем случае C(n, r) = limit(GAMMA(N+1)/ GAMMA(R+1)/GAMMA(N-R+1),R=r,N=n). • composition(n, k) — возвращает списки композиций для целых неотрицательных n и k; • fibonacci(n) — возвращает числа Фибоначчи, вычисляемые по рекуррентной формуле F(n) = F(n–1)+F(n–2), где F(0) = 0 и F(1)=1; • fibonacci(n, х) —возвращает значение полинома Фибоначчи F(n, х) = х F(n–1, х) + F(n–2, х), где F(0, х)–0 и F(1, а)=1, при этом F(n)=F(n, 1); • firstpart(n) — возвращает первый член последовательности из наборов чисел, сумма которых равна n (в оригинале каноническую последовательность); • nextpart(1) — возвращает следующую часть указанной выше последовательности; • lastpart(n) — возвращает последний член последовательности, указанной для функции firstpart; • prevpart(1) — возвращает предпоследнюю часть канонической последовательности ряда; • conjpart(1) — возвращает объединенный раздел в канонической последовательности ряда; • graycode(n) — возвращает список кодов Грея для n-битовых чисел; • multinomial(n, k1, k2,…, km) — возвращает мультиномиальные коэффициенты; • numbcomb(n) и numbcomb(n, m) — возвращает число комбинаций; • numbcomp(n, k) — возвращает число различных упорядоченных наборов из к натуральных чисел, сумма которых равна n; • numbpart(n) — возвращает список всех возможных сумм, дающих n; • permute(n) и permute(n, r) — возвращает numbperm(n, r) = nops(permute(n, r)); • powerset(s) — возвращает степень множества в множестве s; • randcomb(n, m) — возвращает случайную комбинацию; • randpart(n) — возвращает случайную часть: • randperm(n) — возвращает случайную композицию; • stirling1(n, m) — возвращает число Стирлинга первого рода; • stirling2(n, m) — возвращает число Стирлинга второго рода; • subsets(L) — задает итерационную процедуру над степенями множества или списка L; • vectoint(I) — возвращает индекс вектора канонического упорядочения I; • inttovec(m, n) — возвращает вектор канонического упорядочения для неотрицательных целых чисел m и n. Следующие примеры (файл combinat) иллюстрируют применение функций комбинаторики: > choose(4,3);[[1,2,3], [1, 2, 4], [1,3,4], [2, 3, 4]] > choose([a,a,b,с],3);[[a,a,b], [a,a,с],[a,b,c]] > composition(3,2);{[2, 1], [1,2]} > decodepart(4,2);[1,1,2] > fibonacci(10);55 > seq(fibonacci(i),i=1..12);1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 > partition(5);[[1, 1, 1, 1, 1], [1, 1, 1, 2], [1, 2, 2], [1, 1, 3], [2, 3], [1, 4], [5]] > firstpart(3);[1, 1, 1] > nextpart(%);[1,2] > prevpart(%);[1, 1, 1] > lastpart(3);[3] > conjpart(%);[1, 1, 1] > multinomial(8,2,3,3);560 > numbcomp(8,5);35 > numpart(3);numpart(3) > numbperm(4);24 > numbperm([a, b]);2 > numbperm({a,b,c}, 2);6 > permute(3,2);[[1,2], [1,3], [2, 1], [2, 3], [3, 1], [3, 2]] > permute([a,a,b],2);[[a,.a], [a,b], [b,a]] > powerset([a,a,b]);[[ ], [a], [b], [a,b], [a,a], [a,a,b]] > randcomb([a,b,c,d],3);[a,c,d] > randcomb([a, b, c, d], 3);[a,b,d] > randpart(10);[2, 8] > randpart(10);[10] > stirling1(10,5);-269325 > stirling2(10, 5);42525 > S:=subsets({1,2}): > while not S[finished] do S[nextvalue]() od;{ } {1} {2} {1,2} > vectoint([1,0,0]);1 > inttovec(6,3);[1,0,1] 3.4.2. Функции пакета структур комбинаторики combstructЕще девять функций, относящихся к структурам комбинаторики, содержит пакет combstruct: > with(combstruct);[agfeqns, agfmomentsolve, agfseries, allstructs, count, draw, finished, gfeqns, gfseries, gfsolve, iterstructs, nextstruct] Эти функции служат для создания случайно однородных объектов, принадлежащих заданному комбинаторному классу. Ограничимся приведением примеров применения этих функций (файл combictruct): > allstructs(Subset({one,two)));{{ }, {one, two), {two}, {one)} > allstructs(Permutation([x,y,z]),size=2);[[x,y], [x,z], [x,y], [y,z], [z,x], [z,y]] > count(Subset({1,2,3}));8 > draw(Combination(5),size=4);{1, 3, 4, 5} > count(Permutation([a,a,b])); > it :=iterstructs(Permutation([a,a,b]),size=2);it:= table([finished = false, nextvalue = (proc(0) ... end proc)|) > draw(Partition(9));[2, 2, 2, 3] > allstructs(Composition(3), size=2);[[2, 1], [1,2]] 3.4.3. Функции пакета теории чисел — numtheoryВ обширном пакете numtheory собран ряд функций, относящихся к теории чисел. Их можно просмотреть, используя команду: > with(numtheory); Большинство функций этого пакета достаточно просты и заинтересовавшийся читатель вполне в состоянии провести их тестирование самостоятельно. 3.4.4. Пакет для работы с р-адическими числами — padicЭтот весьма специфический пакет содержит следующие функции для работы с р-адическими числами. Команда > with(padic); Выводит список имен этого пакета. Ввиду специфичности данных функций их изучение мы оставляем за читателем для самостоятельной работы — если она требует применения таких чисел. 3.4.5. Пакет для работы с гауссовыми целыми числами — GaussIntГауссово целое число — это число вида а+I*b, где а и b — любые целые рациональные числа. Таким образом они образуют решетку всех точек с целыми координатами на плоскости комплексных чисел. Пакет GaussInt содержит достаточно представительный набор функций для работы с этими числами: > with(GaussInt); Warning, the name Glgcd has been redefined[GIbasis, GIchrem, GIdivisor, GIfacpoly, GIfacset, GIfactor, GIfactors, GIgcd, GIgcdex, GIhermite, GIissqr, GIlcm, GImcmbine, GInearest, GInodiv, GInorm, GInormal, GIorder, GIphi, GIprime, Glquadres, GIquo, GIrem, GIroots, GIsieve, GIsmith, GIsqrfree, GIsqrt, GIunitnormal] Нетрудно заметить, что в этот набор входят уже известные числовые функции, к именам которых добавлены буквы GI. Например, функция GIfactor(c) раскладывает гауссово число (в том числе комплексное) на простые множители, GIgcd(c1,c2) находит наибольший общий делитель гауссовых чисел с1 и с2 и т.д. В связи с этим в особых комментариях пакет не нуждается. 3.5. Расширенные возможности Maple в работе с выражениями3.5.1. Ввод выраженийФактически Maple — это система для манипулирования математическими выражениями. Выражение в системе Maple — объект, вполне соответствующий сути обычного математического выражения. Оно может содержать операторы, операнды и функции с параметрами. Выражения в Maple могут оцениваться и изменяться в соответствии с заданными математическими законами и правилами преобразований. Например, функция упрощения выражений simplify способна упрощать многие математические выражения. Maple автоматически упрощает некоторые выражения, например, такие, как х+0, х-0, 1*х, х/1 и т.д. Но функцию можно применять и для выражений, записанных в качестве ее параметра в круглых скобках (файл expr): > simplify(sin(х)^2+cos(х)^2) ;1 > simplify((х^2-2*х*а+а^2)/(х-а));x-а Важно отметить, что один и тот же результат может быть получен от многих выражений. Поэтому получение исходного выражения по упрощенному возможно далеко не всегда, а чаще всего просто вообще невозможно. Для выполнения любых математических операций необходимо обеспечить ввод в систему исходных данных — в общем случае математических выражений. Для ввода их и текстовых комментариев служат два соответствующих типа строк ввода. Переключение типа текущей строки ввода осуществляется клавишей F5. Строка ввода математических выражений имеет отличительный символ >, а строка ввода текстов такого признака не имеет. В строке ввода может располагаться несколько выражений. Фиксаторами (указанием, что выражение окончено) их могут быть символы ; (точка с запятой) и : (двоеточие). Символ «;» фиксирует выражение и задает вывод результатов его вычисления. А символ «:» фиксирует выражение и блокирует вывод результатов его вычисления. Фиксаторы выполняют также функцию разделителей выражений, если в одной строке их несколько. Ввод выражения оканчивается нажатием клавиши Enter. При этом маркер ввода (жирная мигающая вертикальная черта) может быть в любой позиции строки. Если надо перенести ввод на новую строку, следует нажимать клавиши Shift и Enter совместно. С помощью одного, двух или трех знаков % (в реализациях до Maple V R5 это был знак прямых кавычек ") можно вызывать первое, второе или третье выражение с конца сессии (файл expr): > а:b:с: > %;с > а:b:с: > %%;b > a:b:c: > %%%;a > 2+3: > %;5 > %%+5;10 Особая роль при вводе выражений принадлежит знакам прямого апострофа (одиночного ' или двойного "). Заключенное в такие знаки выражение освобождается от одной пары (закрывающего и открывающего знаков '): > ''factor(а^2+2*а*b^2+b^2)'';'factor(a² +2 ab² +b²)' > %;factor(a² +2 ab² +b²) > factor(а^2+2*а*b+b^2);(a + b)² Некоторые другие возможности обрамления выражений апострофами мы рассмотрим позже. Наиболее важная из них — временная отмена выполненного ранее присваивания переменным конкретных значений. Для завершения работы с текущим документом достаточно исполнить команду quit, done или stop, набранную в строке ввода (со знаком ; в конце). 3.5.2. Оценивание выраженийВстречая выражение, Maple оценивает его, то есть устанавливает возможность его вычисления и, если возможно, вычисляет его. Если выражение — скалярная переменная, то ее значение будет выведено в ячейке вывода. Для переменных более сложных типов выводится не их значение, а просто повторяется имя переменной. Просто повторяются также имена неопределенных переменных. Для оценивания выражений различного типа существует группа функций, основные из которых перечислены ниже: • eval(array) — возвращает вычисленное содержимое массива array; • evalf(expr, n) — вычисляет expr и возвращает вычисленное значение в форме числа с плавающей точкой, имеющего n цифр после десятичной точки; • evalhf(expr) — вычисляет expr и возвращает вычисленное значение с точностью, присущей оборудованию данного компьютера; • evalf(int(f, x=a..b)) — оценивает и возвращает значение определенного интеграла int(f,x=a..b); • evalf(Int(f, x=a..b)) — оценивает и возвращает значение определенного интеграла, заданного инертной функцией Int(f,x=a..b); • evalf(Int(f, x=a..b, digits, flag)) — аналогично предыдущему, но возвращает значение интеграла с заданным параметром digits числом цифр после десятичной точки и со спецификацией метода вычислений flag; • evalm(mexpr) — вычисляет значение матричного выражения mexpr и возвращает его; • evalb(bexpr) — вычисляет и возвращает значения логических условий; • evalc(cexpr) — вычисляет значение комплексного выражения; • evalr(expr, ampl) — оценивает и возвращает значения интервальных выражений (функция должна вызываться из библиотеки); • shake(expr, ampl) — вычисляет интервальное выражение. Для функции evalf параметр n является необязательным, при его отсутствии полагается n=10, то есть вещественные числа по умолчанию выводятся с мантиссой, имеющей десять цифр после десятичной запятой. В выражении expr могут использоваться константы, например, Pi, ехр(1), и функции, такие как ехр, ln, arctan, cosh, GAMMA и erf. В матричном выражении mexpr для функции evalm могут использоваться операнды в виде матриц и матричные операторы &*, +, - и ^. В комплексных выражениях cexpr наряду с комплексными операндами вида (а+I*b) могут использоваться многие обычные математические функции: Sin cos tan csc sec cot Sinh cosh tanh csch sech coth Arcsin arccos arctan arccsc arcsec arccot Arcsinh arccosh arctanh arccsch arcsech arccoth Exp ln sqrt ^ abs conjugate Polar argument signum csgn Re Im Ei LambertW dilog surd Примеры применения функций оценивания даны ниже (файл eval): > А: = [[1,2],[3,4]];А:= [[1,2], [3, 4]] > eval(А);[[1,2], [3, 4]] > evalf(sin(1));.8414709848 > evalf(sin(2)^2+cos(2)^2,20);1.0000000000000000000 > evalhf(sin(1));.841470984807896505 > evalm(20*A+1); 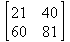 > 1<3;1<3 > evalb(1<3);true > readlib(shake) : evalr(min(2,sqrt(3) )) ;√3 > evalr(abs(x));INTERVAL(INTERVAL(, 0..∞), -INTERVAL(, -∞..0)) > shake(Pi,3);INTERVAL(3.1102..3.1730) В дальнейшем мы многократно будем применять функции оценивания для демонстрации тех или иных вычислений. 3.5.3. Последовательности выраженийMaple может работать не только с одиночными выражениями, но и с последовательностями выражений. Последовательность выражений — это ряд выражений, разделенных запятыми и завершенный фиксатором (файл expr1): > a, y+z, 12.3, cos(1.0);a, y + z, 12.3, .5403023059 Для автоматического формирования последовательности выражений применим специальный оператор $, после которого можно указать число выражений или задать диапазон формирования выражений: > f$5;f,f,f,f,f > $1..5;1, 2, 3, 4, 5 > (n^2)$5;n², n², n², n², n² > (n^2)$n=0..5;0, 1, 4, 9, 16, 25 > Vl[i]$i=1..5;Vl1, Vl2, Vl3, Vl4, Vl5 Для создания последовательностей выражений можно использовать также функцию seq: > seq(sin(х),х=0..5);0, sin(1), sin(2), sin(3), sin(4), sin(5) > seq(sin(x*1.),x=0..5);0., .8414709848, .9092974268, .1411200081, -.7568024953, -.9589242747 > seq(f1(1.),f1=[sin,cos,tan]);.8414709848, .5403023059, 1.557407725 > sin(1.0), cos(1.0), tan(1.0);.8414709848, .5403023059, 1.557407725 3.5.4. Вывод выраженийПри выполнении порой даже простых операций результаты получаются чрезвычайно громоздкими. Для повышения наглядности выражений Maple выводит их с выделением общих частей выражений и с присваиванием им соответствующих меток. Метки представлены символами %N, где N — номер метки. Помимо меток при выводе результатов вычислений могут появляться и другие специальные объекты вывода, например корни RootOf, члены вида O(x^n), учитывающие погрешность при разложении функций в ряд, и обозначения различных специальных функций, таких как интегральный синус, гамма-функция и др. Примеры такого вывода приведены ниже: > solve(х^7-х^2-1,х);½+½I√3, ½-½I√3, RootOf(_Z5 + _Z4 - _Z2 - _Z - 1, index = 1), RootOf(_Z5 + _Z4 - _Z2 - _Z - 1, index = 2), RootOf(_Z5 + _Z4 - _Z2 - _Z - 1, index = 3 ), RootOf(_Z5 + _Z4 - _Z2 - _Z - 1, index = 4), RootOf(_Z5 + _Z4 - _Z2 - _Z - 1, index = 5) > taylor(sin(x),x,5); 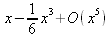 Часто встречаются также знаки ~ для отметки предполагаемых переменных, постоянные интегрирования и другие специальные обозначения. По мере упоминания в тексте таких объектов вывода они будут описаны. 3.5.5. Работа с частями выраженийВыражения (expr) или уравнения (eqn) обычно используются как сами по себе, так и в виде равенств или неравенств. В последнем случае объекты с выражениями имеют левую и правую части. Для простейших манипуляций с выражениями полезны следующие функции: • cost(a) — возвращает число сложений и умножений в выражении а (функция пакета codegen); • lhs(eqn) — выделяет левую часть eqn; • rhs(eqn) — выделяет правую часть eqn; • normal(expr) — дает нормализацию (сокращение) expr в виде дроби; • numer(expr) — выделяет числитель expr; • denom(expr) — выделяет знаменатель expr. Ввиду очевидности действия этих функций ограничимся наглядными примерами их применения: > with(codegen,cost): > cost(х^3+b^2-х);2 additions + 3 multiplications > lhs(sin(x)^2+cos(x)^2=1);sin(x)² + cos(x)² > rhs(sin(x)^2+cos(x)^2=1);1 > normal(2/4+3/6+6/12); 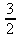 > f:=5*(a-b)^2/(а^2-2*а*b-b^2); 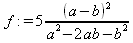 > numer(f);5 (a-b)² > denom(f);a²-2ab-b² Обратите внимание на то, что в старых версиях (до Maple 7) загрузка библиотечной функции cost выполнялась иначе — командой readlib(cost). Это обстоятельство может служить причиной неверной работы документов, созданных в старых версиях Maple, в среде последующих версий Maple. 3.5.6. Работа с уровнями вложенности выраженийВ общем случае выражения могут быть многоуровневыми и содержать объекты, расположенные на разных уровнях вложенности. Приведем две функции для оценки уровней выражений и списков: • nops(expr) — возвращает число объектов первого уровня (операндов) в выражении expr; • op(expr) — возвращает список объектов первого уровня в выражении expr; • op(n,expr) — возвращает n-й объект первого уровня в выражении expr. Ниже представлены примеры применения этих функций: > nops(а+b/с);2 > op(a+b/c); 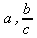 > op(1,a+b/c);а > op(2,a+b/c); 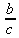 Рекомендуется просмотреть и более сложные примеры на применение этих функций в справке. 3.5.7. Преобразование выражений в тождественные формыМногие математические выражения имеют различные тождественные формы. Порою преобразование выражения из одной формы в другую позволяет получить результат, более удобный для последующих вычислений. Кроме того, различные функции Maple работают с разными формами выражений и разными типами данных. Поэтому большое значение имеет целенаправленное преобразование выражений и данных. Основной функцией для такого преобразования является функция convert: convert(expr, form, arg3,...) Здесь expr — любое выражение, form — наименование формы, arg3, … — необязательные дополнительные аргументы. convert — простая и вместе с тем очень мощная функция. Ее мощь заключается в возможности задания множества параметров. Их полный перечень (около восьмидесяти наименований) можно найти в справке по функции convert. Многие из этих параметров очевидны с первого взгляда, поскольку повторяют наименования типов чисел, данных или функций. Например, опции binary, decimal, hex и octal преобразуют заданные числа в их двоичное, десятичное, шестнадцатиричное и восьмеричное представление. Параметр vector задает преобразование списка в вектор (напоминаем, что список и вектор — разные типы данных), а параметр matrix — в матрицу. Приведем примеры применения функции convert (файл expr1): > convert(123,binary);1111011 > convert([a,b,с,d],`+`);a + b + c + d > f:=seq(x[i]^n,i=1..4);f:=x1n, x2n, x3n, x4n > x:='x'; convert(sinh(x),ехр);x:= x 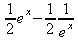 > convert(1.234567,fraction); 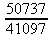 > convert(1/7,float);.1428571429 > convert(sin(I*x),exp); 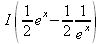 > convert(sinh(x),exp); 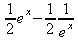 > convert(arcsinh(x),ln); 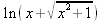 > convert(12345,list);[12345] > convert(binomial(m,n),factorial); 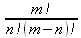 > convert([[1,2],[3,4],[5,6]],table);table([(1, 1) = 1, (2, 1) = 3, (2, 2) = 4, (3, 1) = 5, (3, 2) = 6, (1, 2) = 2]) > convert(-Pi,signum);-π > s:=taylor(sin(x),x,8); 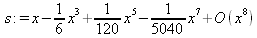 > p:=convert(s,polynom); 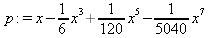 > convert(p,float);x-.1666666667x3 +.008333333333x5 -.0001984126984x7 > f:=(х^4+х)/(x^2-1); 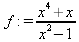 > convert(f, parfrac, x); 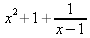 > s:=series(f,x,5);s:= -x - x3 -x4 + O(x5) > convert(s,polynom);# Удаление члена ряда, описывающего погрешность-х - х3 - х4 Из этих примеров (их список читатель может пополнить самостоятельно) следует, что функция преобразования convert является одной из самых мощных функций Maple. С ее помощью можно получить множество различных форм одного и того же выражения. 3.5.8. Преобразование выраженийЕще одним мощным средством преобразования выражений является функция combine. Она обеспечивает объединение показателей степенных функций и преобразование тригонометрических и некоторых иных функций. Эта функция может записываться в трех формах: combine(f) combine(f, n) combine(f, n, opt1, opt2,...) Здесь f — любое выражение, множество или список выражений; n — имя, список или множество имен; opt1, opt2, … — имена параметров. Во втором аргументе можно использовать следующие функции: @@ abs arctan conjugate ехр ln piecewise polylog power product Psi radical range signum trig Примеры применения функции combine представлены ниже (файл expr1): > combine(ехр(2*х)^2,ехр);е(4x) > combine(2*sin(х)^2+2*cos(х)^2);2 > combine(sin(х)*cos(х));½sin(2x) > combine(Int(х,x=a..b)-Int(х^2,x=a..b)); 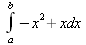 Эти примеры далеко не исчерпывают возможности функции combine в преобразовании выражений. Рекомендуется обзорно просмотреть примеры применения функции combine с разными параметрами, приведенные в справочной системе Maple. 3.5.9. Контроль за типами объектовВыражения и их части в Maple рассматриваются как объекты. В ходе манипуляций с ними важное значение имеет контроль за типом объектов. Одной из основных функций, обеспечивающих такой контроль, является функция whattype(object), возвращающая тип объекта, например string, integer, float, fraction, function и т.д. Могут также возвращаться данные об операторах. Примеры применения этой функции даны ниже (файл control): > whattype(2+3);integer > whattype(Pi);symbol > whattype(123./5);float > whattype(1/3);fraction > whattype(sin(x));function > whattype([1, 2, 3, a, b, c]);list > whattype(a+b+c);+ > whattype(a*b/c);* > whattype(a^b);^ > whattype(1+2+3=4);= С помощью функции type(object,t) можно выяснить, относится ли указанный объект к соответствующему типу t, например: > type(2+3,integer);true > type(sin(х),function);true > type(hello,string);false > type("hello",string);true > type(1/3,fraction);true При успешном соответствии типа объекта указанному (второй параметр), функция type возвращает логическое значение true, в противном случае — false. Для более детального анализа объектов может использоваться функция hastype(expr, t), где expr — любое выражение и t — наименование типа подобъекта. Эта функция возвращает логическое значение true, если подобъект указанного типа содержится в выражении expr. Примеры применения этой функции даны ниже (файл control): > hastype(2+3,integer);true > hastype(2+3/4,integer);false > hastype(2*sin(x),function);true > hastype(a+b-c/d,`+`);true Еще одна функция — has(f,x) — возвращает логическое значение true, если подобъект х содержится в объекте f, и false в ином случае: > has(2*sin(х),2);true > has(2*sin(x), `/`);false > has(2*sin(x),3-1);true Следует отметить, что соответствие подобъекта выражения указанному подобъекту понимается в математическом смысле. Так, в последнем примере подобъект «3-1», если понимать его буквально, в выражении 2*sin(x) не содержится, но Maple-язык учитывает соответствие 3-1=2, и потому функция has в последнем примере возвращает true. Функция has может использоваться для выявления той или иной математической операции, оператора или функции. Однако надо соблюдать определенные правила, поскольку выражение, анализируемое функцией has оценивается и исполняется. Внимательно проанализируете приведенные ниже примеры: > has(2*sin(2),sin);true > has(2*sin(2),'sin');true > has(2*sin(2.), 'sin');false Здесь надо учесть, что выражение 2*sin(2) после оценки и исполнения не меняется, поскольку Maple, при целочисленном аргументе функции синуса, не вычисляет ее и вычисленное выражение совпадает с исходным и содержит функцию синуса. Однако sin(2.) уже вычисляется и становится числом. Именно поэтому в последнем примере функция sin уже не обнаруживается. Подобное имеет место и в ряде других примеров с функцией интегрирования: > has('int(х^2,х)',int);true > has(int(х^2,х),int);false > int(х^2,х); 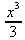 > has(int(х^2,х), х^3/3);rue Столь же поучителен пример с идентификацией функции интегрирования. Так, has(int(х^2, х), int); дает false, поскольку интеграл оценивается и вычисляется, что ведет к подмене выражения на х^3/3 уже не содержащего признаков интегрирования. Это и поясняют два последних примера, в которых вычислено значение интеграла и функция has дает значение true для значения интеграла. В тоже время заключение int(x^2,x) в апострофы позволяет найти имя функции интегрирования int, поскольку исходное выражение в этом случае представлено в неисполняемой форме и содержит обращение к этой функции. Еще одна иногда полезная функция контроля выражений depends(f,x) возвращает true, если х входит в f и false в противном случае. При этом надо также помнить, что функция (выражение) оценивается и исполняется. Следующие примеры хорошо иллюстрируют сказанное: > depends(2+2*sin(x),х);true > depends(int(х^2,х),х);true > depends(int(х^2,х=0..1), х)false В последнем примере вычисленное выражение это уже просто число, в нем х не содержится, а потому и получено значение false. 3.6. Работа с подстановками3.6.1. Функциональные преобразования подвыраженийНередко бывает необходимо заменить некоторое подвыражение в заданном выражении на функцию от этого подвыражения, т.е. осуществить подстановку. Средства для обеспечения подстановок есть во всех СКМ. Так, для этого в Maple 9.5 можно воспользоваться функцией applyop: • applyop(f, i, е) — применяет функцию f к i-му подвыражению выражения е; • applyop(f, i, е…, xk,…) — применяет функцию f к i-му подвыражению выражения е с передачей необязательных дополнительных аргументов xk. Ниже даны примеры применения этой функции (здесь и далее см. файл subs): > restart;applyop(sin,2,a+x);a + sin(x) > applyop(f,1,g,2,a+b);f(g, 2, a + b) > applyop(f,{2,3},a+x+b);a+f(x)+f(b) > applyop(f,{1,2},x/y+z); 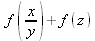 > р:=у^2-2*у-3;p:= y²-2y -3 > applyop (f, 2,p);p:= y² -2y -3 > applyop{f,[2, 3 ], p);y²+f(-2y)-3 > applyop(f,{[2,1],3},p);y² + f(-2y) + f(-3) > applyop(abs,{[2,1],3},p);y²+2y+3 3.6.2. Функциональные преобразования элементов списковЕще две функции, реализующие операции подстановки, указаны ниже: map(fcn, expr, arg2, ..., argn) map2(fcn, arg1, expr, arg3,..., argn) Здесь fcn — процедура или имя, expr — любое выражение, argi — необязательные дополнительные аргументы для fcn. Первая из этих функций позволяет приложить fcn к операндам выражения expr. Приведенные ниже примеры иллюстрируют использование функции map: > f:=х->х^2;f: = х→х² > map(f, [1,2,3]);[1, 4, 9] > map(f,[x,y,z]);[x², y², z²] > map(х->х^n, [1,2,3]);[1, 2n, 3n] > L:=[1,2,3,4];L:=[1, 2, 3, 4] > map(proc(x,y) x*y+1 end,[1, 2, 3, 4], 2);[3, 5, 7, 9] > map(int,L,x);[x, 2x, 3x, 4x] > map(F, [1, 2, 3], x, y, z);[F(3, x, y, z), F(3, x, y, z), F(3, x, у, z)] Из этих примеров нетрудно заметить, что если второй параметр функции map — список, то функция (первый параметр) прикладывается к каждому элементу списка, так что возвращается также список. Из последнего примера видно, что если за вторым параметром идет перечисление аргументов, то они включаются в список параметров функции. Функции map2 отличается иным расположением параметров. Ее действие наглядно поясняют следующие примеры: > map2(w, g, {а,b,с});{w(g, a), w(g, b), w(g, с)} > map2(op,1,[a+b+i,c+d+k, e+f+j]);[а, с, е] > map2(ор,3,[a+b+i,c+d+k,e+f+j]);[i, k, j] > map2(diff,[sin(х),cos(х),x^n],х); 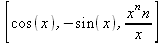 При решении некоторых задач оптимизации возникает необходимость в создании выражений с множителями Лагранжа. Для этого можно использовать список из трех элементов выражения, заключенный в угловые скобки: > е := <х^2, -sqrt(16-х^2), 5>; 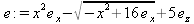 Примеры на работу с выражениями, имеющими множители Лагранжа можно найти в файле демонстрационным L4lagra.mse. 3.6.3. Подстановки с помощью функций add, mul и seqЗаметим, что операции, подобные описанным выше, Maple реализует и с рядом других функций. Ограничимся примерами на подстановки с помощью функций сложения add, умножения mul и создания последовательностей seq: > add(i,i=[a,b,c]);a + b + c > addi=[a,b,c]);a² + b² + c² > add(i^2,i=[1,2,3]);14 > mul(x-i,i=0..4);x(x - 1)(x - 2)(x - 3)(x - 4) > mul(х^i,i=0..4);x10 > seq(w(i),i={a,b,c});w(a), w(b), w(c) > seq(w(x, y, z), i={1,2,3});w(x, y, z), w(x, y, z), w(x, y, z) > seq(int(x^i,x),i={1,2,3,4}); 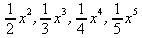 3.6.4. Подстановки с помощью функций subs и subsopПодстановки в общем случае служат для замены одной части выражения на другую. Частными видами подстановок являются такие виды операций, как замена одной переменной на другую или замена символьного значения переменной ее численным значением. Основные операции подстановки выполняют следующие функции: • subs(x=a,e) — в выражении е заменяет подвыражение х на подвыражение а; • subs(s1,…,sn,e) — в выражении е заменяет одни подвыражения на другие, выбирая их из списков s1, sn вида х=а; • subsop(eq1, eq2, …, eqi, …, eqn, e) — в выражении e заменяет указанные в eqi операнды другими, указанными в правой части равенств eqi вида ni=ei, где ni — номер операнда, ei — выражение для замены. Все эти функции возвращают измененное после подстановки выражение. Ниже показаны примеры применения функций подстановок: > subs(а=b,b^2-2*а*b-b^2);-2 b² > subs (а=2,b=1,b^2-2*а*b-b^2); 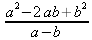 > normal(%);a-b > subs(a=x,b=y,c=z,[a,b,с]);[x, y, z] > subs({x=y,y=x),[x,y]);[y, х] > subs(a=sin(x),b=cos(x),а^2+b*b);sin(x)² + cos(x)² > simplify(%);1 > subsop(1=x,a+b+c);x + b + c > subsop(2=x,a+b+c);a + x + c > subsop(3=x,a+b+c);a + b + x > subsop(3=x,a+b/c); Error, improper op or subscript selector > subsop(1=sin(x),(1+cos(x))/b); 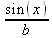 > subsop(2=sin(x),(1+cos(x))/b);(1 +cos(x))sin(x) > subsop(1=sin(x),2=sin(x),(1+cos(x))/b);sin(x)² Следует обратить внимание на то, что результат подстановок, полученный с помощью функции subop, порой может не совпадать с ожидаемым. Поэтому полезно контролировать получаемые в результате подстановок выражения на их корректность. Одним из важных применений подстановок является проверка правильности решений уравнений и систем уравнений. Ниже дан пример такой проверки: > eqs:={x+y+z=6,y/x=z-1,z-x=2}; 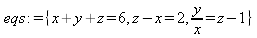 > res:=solve(eqs,{х,у,z});res: = {z = -2, у = 12, x = -4}, {y = 2, z = 3, x = 1} > subs(res,eqs);{2 = 2, 6 = 6, -3 = -3} > subs(c=a-b,(а^2-2*а*b+b^2)/с); Здесь задана система из трех нелинейных уравнений, которая затем решена функцией solve. В конце примера с помощью функции подстановки выполнена проверка правильности решения. Оно верно, поскольку у всех уравнений значение левой части совпадает со значением правой части. 3.6.5. Подстановки правил и подвыраженийДля применения некоторого правила или списка правил rule к некоторому выражению expr используется функция applyrule(rule, expr). Применение этой функции достаточно очевидно: > restart:applyrule(f(а::integer*х)=a*f(х),f(2*х)+g(х)-p*f(х));2f(x)+g(x)-pf(x) > applyrule(х^2=у,f(x^2,ln(cos(x)+2*x^2)));f(y, ln(cos(x) + 2y)) > applyrule(b+c=x,f(a+b+c+d));f(x + a + d) Эта функция более мощная, чем subs, но она не выполняет математические вычисления, подобно тому, как это делает функция algsubs(a=b, f, v, options) с необязательными двумя последними параметрами. Проанализируйте следующие примеры > algsubs(а^2=0, ехр(2-а+а^2/2-а^3/6));e(2-a) > applyrule(а^2=0, ехр(2-a+a^2/2-a^3/6));e(2-a-1/6a³) и различия между этими функциями подстановки станет ясным. 3.6.6. Функции сортировки и селекцииСортировка и селекция выражений широко используются в практике символьных преобразований. Нередко она важна в статистических расчетах, обеспечивая повышение их точности. Для выполнения сортировки служит функция sort, применяемая в одной из следующих форм: sort(L) sort(L, F) sort(A) sort(A, V) Здесь L — список сортируемых значений, F — необязательная булева процедура с двумя аргументами, А — алгебраическое выражение, V — необязательные дополнительные переменные. Примеры применения этих функций (файл sortsel) > restart; > sort([у, s,f,a,c,i] ); t([2,5,1,7,3,8]);[a, c, f, i, s, y] t([2, 5,1,7, 3, 8]) > sort([y,s,f,a,c,i]);[a, c, f, i, s, y] > sort([у,s,f,а,с,i],lexorder);[a, c, f, i, s, y] > sort(1+х^4-х^2+х);x4 - x2 + x + 1 > sort(у*х^2+х*у+у-х^2+х^4*у^5);x4 y5 + x2y - x2 + xy + у > sort((y+z+x)/(y-x-z),{x, y}); 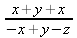 > names:= ["Peter","Anna","Vladimir", "Ivan"];names := ["Peter", "Anna", "Vladimir", "Ivan"] > sort(names);["Anna", "Ivan", "Peter", "Vladimir"] > integers:=[$10..30];integers := [10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30] Если функция сортировки меняет порядок расположения членов в выражении (или порядок расположения выражений), то другая функция — select — служит для выделения требуемого выражения: select(f, е) select(f, е, b1, ..., bn) Как бы обратной ей по действию служит функция remove, устраняющая заданные выражения: remove(f, е) remove(f, е, b1,.... bn) В этих функциях f — процедура, возвращающая логическое значение, е — список, множество, сумма, произведение или функция, b1, …, bn — необязательные дополнительные аргументы. Ниже даны примеры применения этих функций (файл sortsel): > integers := [$10..30]: > select(isprime,integers);[11, 13, 17, 19, 23, 29] > remove(isprime,integers);[10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30] > f:=2*ln(a*x)*exp(x)*ln(y);f: = 2 ln(ax)ex ln(y) > select(has,f,x);ln(ax)ex > remove(has,f,x);2 ln(y) > f:=indets(f);f: = {a, x, y, ex, ln(y), ln(ax)} > select(type,f,name);{a, x, y} > remove(type,f,name);{еx, ln(y), ln(ах)} > f:=2*ln(x)*(y+1);f:= 2 ln(x)(y + 1) > c:=remove(has,f,x);с:= 2y + 2 > f/c; 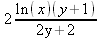 > select(has,f,x);ln(x) Maple имеет также оператор селекции А[expr]. Его действие поясняют следующие примеры (файл sortsel): > restart; > S:=[a+b*c,х^2,с,1,2,3];S:=[a+ bc, x²,c, 1, 2, 3] > S[1];a + bc > S[1..2];[a+bc, x²] > S[-2..-1];[2, 3] > S[3..3];[c] > S[3..2];[] > S[4..6];[1, 2, 3] > X:=S[];X := a + bc, x², c, 1, 2, 3 > X[1];a + bc > X[1..2];a + bc, x² > X[-2..-1];2,3 > S:={a,b,c};S:={a, b, c} > S[1];a > S[3];c > S[1..2];{a, b} > S[-2..-1];{b, c} 3.7. Символьные преобразования выражений3.7.1. Упрощение выражений — simplifyФункция simplify — одна из самых мощных в системах символьной математики. Она предназначена для упрощения математических выражений. «Все гениальное просто» — любим мы повторять, хотя это далеко не всегда так. Тем не менее, стремление представить многие математические выражения в наиболее простом виде поощряется в большинстве вычислений и нередко составляет их цель. В системе Maple функция упрощения используется в следующем виде: • simplify(expr) — возвращает упрощенное выражение expr или повторяет его, если упрощение в рамках правил Maple невозможно; • simplify(expr, n1, n2, …) — возвращает упрощенное выражение expr с учетом параметров с именами n1, n2, … (в том числе заданных списком или множеством); • simplify(expr,assume=prop) — возвращает упрощенное выражение expr с учетом всех условий, представленных равенством или списком равенств. Функция simplify — многоцелевая. Она обеспечивает упрощение математических выражений, выполняя следующие типовые действия (для простоты обозначим их как ->): • комбинируя цифровые подвыражения (3*х*5->15*х, 10*x/5->2*x); • приводя подобные множители в произведениях (х^3*а*х->а*х^4); • приводя подобные члены в суммах (5*х+2+3*х->8*х+2); • используя тождества, содержащие ноль (а+0->а, х-0->х); • используя тождества, содержащие единицу (1*х->х); • распределяя целочисленные показатели степени в произведениях ((3*х*у^3)^2->9*х^2*у^6); • сокращая expr на наибольший общий полиномиальный или иной множитель; • понижая степень полиномов там, где это возможно; • используя преобразования, способные упростить выражения. Несмотря на свою гибкость, функция simplify не всегда способна выполнить возможные упрощения. В этом случае ей надо подсказать, в какой области ищутся упрощения и где можно найти соответствующие упрощающие преобразования. С этой целью в функцию simplify можно включать дополнительные параметры. В качестве параметров могут задаваться имена специальных математических функций и указания на область действия упрощений: BesselI, BesselJ, BesselK, BesselY, Ei, GAMMA, RootOf, LambertW, dilog, exp, ln, sqrt, polylog, pg, pochhammer, trig (для всех тригонометрических функций), hypergeom, radical, power и atsign (для операторов). Полезен также параметр symbolic, задающий формальные символьные преобразования для многозначных функций, например, таких как квадратный корень (примеры из файла simplify): > g:=sqrt(х^2); 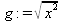 > simplify(g);csgn(x)x > simplify(g,assume=real);|x| > simplify(g,assume=positive);x > simplify(g,symbolic);x Но, чуть иначе: > g:=sqrt(х^у); 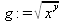 > simplify(g); 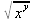 > simplify(g,assume=real); 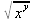 > simplify(g,assume=positive); 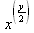 > simplify(g,symbolic); 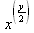 Возможно также применение функции simplify в форме simplify[<name>] где <name> — одно из следующих указаний: atsign, GAMMA, hypergeom, power, radical, RootOf, sqrt, trig. Ниже даны примеры применения функции simplify: > simplify(4^(1/2)+3);5 > simplify((х^у)^z+3^(3),power);(хy)z + 27 > simplify(sin(х)^2+cos(х)^2,trig);1 > e:=cos(х)^5+sin(х)^4+2*cos(х)^2-2*sin(х)^2-cos(2*х);е: = cos(x)5 + sin(x)4 + 2cos(x)2 - 2sin(x)2 -cos(2x) > simplify(e);cos(x)5 + cos(x)4 > simplify(GAMMA(n+4)/GAMMA(n),GAMMA);n(n+1)(n+2)(n+3) > r:=RootOf(х^2-2=0,х): > simplify(r^2,RootOf);2 > simplify(1/r,RootOf);½ RootOf(_Z² - 2) > simplify(ln(x*y),power,symbolic);ln(x) + ln(y) > е:=(-5*b^2*а)^(1/2); 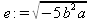 > simplify(e,radical); 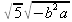 > simplify(e,radical,symbolic); 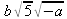 > simplify(GAMMA(n+1)/n!);1 Действие функции simplify существенно зависит от областей определения переменных. В следующем примере упрощение выражения не произошло, поскольку результат этой операции неоднозначен: > restart; > simplify(sqrt(х^4*у^2)); 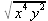 Однако, определив переменные как реальные или положительные, можно легко добиться желаемого упрощения: > simplify(sqrt(х^4*у^2),assume=positive);x² у > simplify(sqrt(х^4*у^2),assume=real);x²|y| С помощью равенств можно задать свои правила преобразования, например: > eq:=x^2+2*x*y+y^2;eq:=х² +2ху + y² > simplify(eq,{х=1));y² + 2y + 1 > simplify(eq,{х^2=х*у, у^2=1});3хy + 1 > simplify(eq,{х,у});0 Обратите внимание на то, что указание в списке равенств только левой части равенства означает, что правая часть принимается равной нулю. Если функция simplify не способна выполнить упрощение выражения expr, то она просто его повторяет. Это сигнал к применению опций, уточняющих преобразования. Сложность упрощаемых выражений зависит от объема ОЗУ и вида интерфейса. Очень большие выражения надо разбивать на подвыражения и работать с ними раздельно. 3.7.2. Расширение выражений — expandДаже в жизни мы говорим: «не все так просто». Порою упрощенное выражение скрывает его особенности, знание которых является желательным. В этом случае можно говорить о полезности расширения или раскрытия выражения. Функция expand «расширяет» выражение expr и записывается в виде expand(expr, expr1, expr2, ..., exprn) где expr — расширяемое выражение, expr1, expr2, …, exprn — необязательные подвыражения — опции. Имеется также инертная форма данной функции — Ехpand(expr). Кроме того, возможно применение операторной конструкции frontend(expans,[expr]). Функция expand раскладывает рациональные выражения на простые дроби, полиномы на полиномиальные разложения, она способна раскрыть многие математические функции, такие как sin, cos, tan, sinh, cosh, tanh, det, erf, exp, factorial, GAMMA, ln, max, min, Psi, binomial, sum, product, int, limit, bernoulli, euler, abs, signum, pochhammer, polylog, BesselJ, BesselY, BesselI, BesselK, AngerJ, Beta, Hankel, Kelvin, Struve, WeberE и функция piecewise. С помощью дополнительных аргументов expr1, expr2, …, exprn можно задать расширение отдельных фрагментов в expr. Примеры применения функции expand приведены ниже (файл expand): > expand((х+2)*(х+3)*(х+4));x³ + 9х² + 26х + 24 > expand(sin(2*х));2sin(x)cos(x) > expand(sin(х+у));sin(x)cos(y) +cos(x)sin(y) > expand([(a+b)*(a-b),tan(2*x)]); 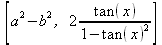 > expand((a+d)*(b+d)*(c+d));abc + abd + adc + ad² + dbc + d²b + d²с = d³ > expand((х+1)*(y+1));xy + х + у + 1 > expand((у+1),(х+1));y + 1 > expand( (х+1) *(у+z));ху + xz + y +z > expand((х+1)*(y+z), х+1);(х + 1)y +(х + 1)z > frontend(expand,[(a+b)^3]);а³ + 3a²b + 3аb²+b³ 3.7.3. Разложение целых и рациональных чисел — ifactorДля разложения целых или рациональных чисел на множители в виде простых чисел служит функция ifactor(n) или ifactor(n,method) где n — число, method — параметр, задающий метод разложения. Другая библиотечная функция, ifactors(n), возвращает результат разложения в форме вложенных списков (файл factor): > ifactor(123456789);(3)² (3803) (3607) > ifactor(30!);(2)26 (3)14 (5)7 (7)4 (11)2 (13)2 (17) (19) (23) (29) > ifactor(12!/20!); 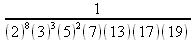 > ifactor(100/78); 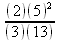 > readlib(ifactors): > ifactors(100/78);[1,[[2, 1], [5, 2], [3,-1], [13,-1]]] 3.7.4. Разложение выражений (факторизация) — factorДля алгебраических выражений функция факторизации записывается в вычисляемой и невычисляемой (инертной) формах: factor(a) Factor(a) factor(a,K) Factor(a,K) Здесь а — полином с несколькими переменными, К — необязательное алгебраическое расширение. Для получения результата от инертной формы функции факторизации надо использовать функции вычисления evala или evalgf. Главная цель факторизации — это нахождение максимального числа независимых сомножителей выражения, линейных по заданным переменным с коэффициентами наиболее простой формы. Ниже представлены примеры применения функции factor: > factor(а^2+2*а*b+b^2);(а+b)² > factor(а^2-2*а*b-b^2);а² - 2ab - b² > p:=expand((х-1)*(х-2)*(х-3)*(х-4));р: = х4 - 10х3 + 35х2 - 50х + 24 > factor(р);(х-1)(х-2)(х-3)(х-4) > factor(х^5-2,2^(1/5));(х -2(1/5))(х4 + х32(1/5) + х22(2/5) + х22(3/5) + 24/5)) > alias(alpha=RootOf(х^2-2));α > factor(х^2-2,alpha);(х + α)(х - α) > factor(х^3-у^3);(х - у)(х² + ху + y²) > factor(х^3-у^3, (-2)^(1/2));(x - y)(x² + ху + y²) > factor(х^3-у^3, (-3)^(1/2)); 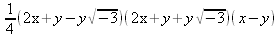 > factor(х^3-3,complex);(х+.7211247852 + 1.249024766I)(х+.7211247852 - 1.249024766I) (х - 1.442249570) 3.7.5. Комплектование по степеням — collectЕще одна функция общего назначения — collect — служит для комплектования выражения expr по степеням указанного фрагмента х (в том числе множества либо списка). Она задается в одной из следующих форм: collect(а, х) collect(а, х, form, func) Во второй форме этой функции дополнительно задаются параметры form (форма) и func (функция или процедура). Параметр form может иметь два значения: recursive (рекурсивная форма) и distributed (дистрибутивная форма). Параметр func позволяет задать имя функции, по которой будет идти комплектование expr. Примеры применения функции collect представлены ниже (файл collect): > collect(х+х^3-2*х,х);-x + x³ > collect(х+2*у^3+х+3+х^3*у,recursive, х);х(2х + 2у³ + 3 + х³y) > collect(х+2*у^3+х+3+х^3*у,distributive,у);у(2х + 2y³ + 3 + х³y) > f:=а*ехр(х)-ехр(х)*х-х;f: = аех - еx - х > collect(f,ехр(х));(а - х)ех - х > g:=int(х*(ехр(х)+ехр(-х)),х); 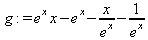 > collect(g,ехр(х)); 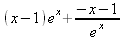 > р:=х*у+а*х*у+у*х^2-а*у*х^2+х+а*х;р:= ху + аху + уx² - аух² + х + ах > collect(р,[х,у],recursive);(1 - а)ух² + ((1 + а)у + 1 + а)х > collect(р,[х,у],distributed);(1 +а)х + (1 + а)ху + (1 - а)ух² > f:=а^3*х^2-х+а^3+а;f:= а³х² - х + а³ + а > collect(f,х);а³х² - х + а³ + а > collect(f,х,factor);а³х² - х + а(а² + 1) > p:=y/x+2*z/x+x^(1/3)-у*х^(1/3); 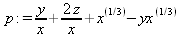 > collect(р,х); 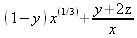 3.7.6. Работа с пакетом рациональных нормальных форм RationalNormalFormsВ Maple входит пакет рациональных нормальных форм RationalNormalForms: > with(RationalNormalForms);[AreSimilar, IsHypergeometricTerm, MinimalRepresentation, PolynomialNormalForm, RationalCanonicalForm] Этот пакет обеспечивает следующие возможности: • конструирование полиномиальных нормальных форм рациональных функций; • конструирование рациональных канонических форм для рациональных функций; • конструирование минимальных представлений для гипергеометрических термов. Ввиду очевидности названий функций этого пакета ограничимся примерами его применения (файл rnform): > F := (n^2-2)*(3*n+3)!/((n+3)!*(2*n+5)!); 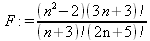 > IsHypergeometricTerm(F,n,'certificate');true > certificate; 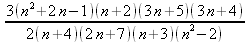 > (z,r,s,u,v) := RationalCanonicalForm[1](certificate,n); 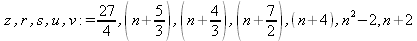 > MinimalRepresentation[1](F,n,k); 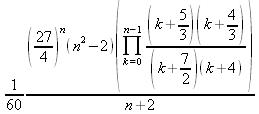 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Главная | В избранное | Наш E-MAIL | Добавить материал | Нашёл ошибку | Наверх | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
