|
||||||||
|
|
Глава 4Практика математического анализа Математический анализ — одна из самых благодатных областей применения систем компьютерной алгебры [36–46]. В этой главе описано решение с помощью СКА Maple наиболее важных задач математического анализа. Особое внимание в этой главе уделено визуализации записи исходных выражений и результатов вычислений, а также проверке последних. 4.1. Вычисление сумм последовательностей4.1.1. Основные функции для вычисления сумм последовательностейНачнем рассмотрение задач математического анализа с вычисления сумм последовательностей. Вычисление суммы членов некоторой последовательности f(k) при изменении целочисленного индекса k от значения m до значения n с шагом +1, то есть выражения 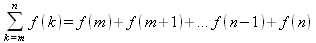 является достаточно распространенной операцией математического анализа. Для вычисляемой и инертной форм сумм последовательностей служат следующие функции: sum(f,k); sum(f,k=m..n); sum(f,k=alpha); Sum(f,k); Sum(f,k=m..n); Sum(f,k=alpha). Здесь f — функция, задающая члены суммируемого ряда, k — индекс суммирования, тип — целочисленные пределы изменения k, alpha — RootOf-выражение. Значение n может быть равно бесконечности. В этом случае для n используется обозначение ∞ или infinity. Допустимо (а зачастую рекомендуется с целью исключения преждевременной оценки суммы) заключение f и k в прямые кавычки — например, sum('f', 'k'=m..n). Рекомендуется все примеры проверять после команды restart, убирающей предыдущие определения f и k. Внимание! При вычислении сумм (и произведений) последовательностей надо строго соблюдать прямой (нарастающий) порядок задания значений индексной переменной суммы. Нарушение этого порядка чревато грубыми ошибками. Так что правила о том, что при измени порядка суммируемых или умножаемых членов последовательности сумма и произведения не меняются в данном случае не поддерживаются на программном уровне. 4.1.2. Последовательности с заданным числом членовПростейшими являются суммы последовательностей с фиксированным числом членов. Ниже даны примеры применения этих функций (файл sum): > restart;k:=2;k:= 2 > Sum(k^2,k=1..4); 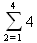 > sum(k^2,k=1..4); Error, (in sum) summation variable previously assigned, second argument evaluates to k=1..4 > sum('k^2','k'=1..4);30 > sum(1/i,i=1..100); 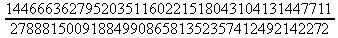 > evalf(%);5.187377518 Обратите внимание, что во втором примере система отказалась от вычисления, а в третьем даже выдала сообщение об ошибке, связанную с тем, что переменной k перед вычислением сумм было присвоено численное значение 2. После заключения выражения и переменной индекса k в прямые кавычки ошибка исчезла, поскольку такая операция означает, что переменной придается неопределенное значение. 4.1.3. Суммы с известным пределомОсобый класс образуют последовательности, у которых существует их предел в аналитическом виде. Ниже представлен ряд последовательностей, у которых переменная индекса задается как 0..n или 1..n (файл sum): > restart; > sum(k, k=1..n); 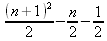 > sum(i/(i+1),i=0..n);n + 1 - Ψ(n +2) - γ > sum(k*binomial(n,k),k=0..n); 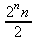 Некоторые из таких сумм выражаются через специальные математические функции. 4.1.4. Суммы бесконечных рядовМногие суммы бесконечных рядов сходятся к определенным численным или символьным значениям, и система Maple способна их вычислять. Это поясняют следующие примеры (файл sum): > restart; > sum(-exp(-k), k); 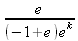 > sum(k*a^k,k); 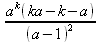 > sum(1/k!,k=0..infinity);e > Sum(1/i^2, i=1..infinity) = sum(1/i^2, i=1..infinity); 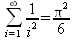 > Sum(1/n!, n=1..infinity) = sum(1/n!, n=1..infinity); 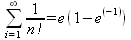 > evalf(%);1.718282828 = 1.718281828 > Sum(1/i^2, i)=sum(1/i^2, i); 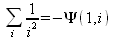 4.1.5. Двойные суммыМогут встречаться множественные суммы по типу «сумма в сумме». Ограничимся приведением примера двойной суммы, имеющей аналитическое значение (файл sum): > Sum(Sum(k^2, k = 1..m), m = 1..N); factor(simplify(value(%))); 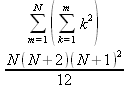 При конкретном значении N такую сумму нетрудно вычислить подстановкой: > subs(N = 100, %);8670850 Как видно из приведенных примеров, средства вычисления сумм последовательностей Maple 9.5/10 позволяют получать как численные, так и аналитические значения сумм, в том числе представляемые специальными математическими функциями. 4.1.6. Пакет вычисления специальных сумм sumtoolsВозможности вычисления специальных сумм существенно расширяются при использовании инструментального пакета вычисления специальных сумм sumtools. При его вызове выводится список функций пакета: > with(sumtools);[Hypersum, Sumtohyper, extended_gosper, gosper, hyperrecursion, hypersum, hyperterm, simpcomb, sumrecursion, sumtohyper] Назначение функций данного пакета перечислено ниже: hypersum(U, L, z, n) и Hypersum(U, L, z, n) — вычисление гиперсумм; sumtohyper(f, k) и Sumtohyper(f, k) — преобразование сумм в гиперсуммы; extended_gosper(f, k), extended_gosper(f, k=m..n) и extended_gosper(f, k, j) — реализация расширенного алгоритма Госпера; gosper(f, k) и gosper(f, k=m..n) — реализация алгоритма Госпера; hyperrecursion(U, L, z, s(n)) — реализация гиперрекурсионного алгоритма; hyperterm(U, L, z, k) и Hyperterm(U, L, z, k) — ввод гипергеометрического терма. 4.1.7. Примеры вычисления специальных суммПриведем примеры на вычисление специальных сумм с помощью функций пакета sumtools (файл sumtools): > extended_gosper(k*(k/2)!, k); 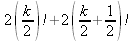 > extended_gosper(k*(k/2)!,k,2); 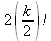 > extendedgosper(k*(k/2)!,k=1..n); 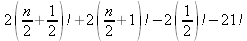 > gosper(k*(k/2)!,k);FAIL > gosper(pochhammer(k,n),k); 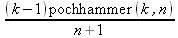 > hyperrecursion([-n,a],[b],1,f(n));(-n + a = b + 1)f(n - 1) + (n + b - 1)f(w) > Hypersum([a,1+a/2,b,c,d,1+2*a-b-c-d+n, -n], [a/2,1+a-b,1+a-c,1+a-d,1+a-(1+2*a-b-c-d+n),1+a+n],1,n);Hyperterm([1, 1+a, a-d-c+1, a+1-d-b, a-с+1-b], [1+a-d, 1+a-c, 1+a-b, a-b-c-d+1, 1, n]) > simpcomb(binomial(n,k)); 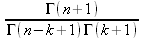 > sumrecursion(binomial(n,k)^3,k, f(n));-8(n - 1)²f(n - 2) - (7n² - 7n + 2)f(n - 1) + f(n)n² > hyperterm([a,b], [c],z,k); 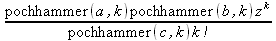 Из этих примеров применение функций данного пакета достаточно очевидно. 4.2. Вычисление произведений членов последовательностей4.2.1. Основные функции для произведения членов последовательностейАналогичным образом для произведений членов f(i) некоторой последовательности, например вида 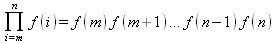 используются следующие функции: product(f, k); product(f, k=m..n); product(f, k=alpha); Product(f, k); Product(f, k=m..n); Product(f, k=alpha). Обозначения параметров этих функций и их назначение соответствуют приведенным для функций вычисления сумм. Это относится, в частности, и к применению одиночных кавычек для f и k. 4.2.2. Примеры вычисления произведений членов последовательностейПримеры применения функций вычисления произведений даны ниже (файл product): > restart; > Product(k^2,k=1..5)=product(k^2, k=1..5); 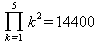 > Product(k^2, k)=product(k^2,k) 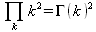 > product(а[k],k=1..5);a1 а2 а3 а4 a5 > f:= [1, 2, 3, 4, 5];f:=[1, 2, 3, 4, 5] > product(f[k],k=1..4);24 > product(n+k,k=1..4);(n + 1)(n + 2)(n + 3)(n +4) > Product(n+k,k=1..m)=product(n+k,k=1..m); 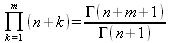 > product(k,k=RootOf(x^3-9));9 Как и в случае вычисления сумм, вычисление произведений возможно как в численной, так и в аналитической форме — разумеется, если таковая существует. Это показывают следующий пример: > Product(2/i,i=1..infinity)=product(2/i,i=1..infinity); 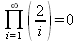 Нетрудно понять, что при i, стремящемся к бесконечности, перемножаемые члены последовательности стремятся к нулю, а потому к нулю стремится и их произведение. 4.3. Вычисление производных4.3.1. Определение производной и полного дифференциалаЕсли f(x) непрерывная функция аргумента х, то производная этой функции Как известно, значение производной геометрически характеризуется наклоном касательной к графику f(х) в точке x=0. Простейший способ наблюдать построение касательной к заданной точке функции заключается в применении функции showtangent из пакета student. Например, команды > with(student): showtangent(sin(x), x = 1.7); строят график синусоиды и касательной к ней в точке х=1.7. Помимо производной, часто встречается понятие дифференциала df(x) =f'(x)∙∆x,то есть произведения производной функции на приращение ее аргумента Δx→0. Производная от производной f(x), то есть функция f''(x) называется производной второго порядка. Могут быть производные третьего, четвертого и так далее, словом производные высшего порядка. Все математические системы способны вычислять такие производные, как и первую производную f'(x) от функции f(x). Довольно часто встречаются функции ряда переменных, например f(x, у, z, …). В этом случае может идти речь о частных производных по переменным х, у, z, …. Например, частной производной по переменной х будет выражение: 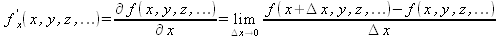 Подобные выражения нетрудно составить и для частных производных по другим переменным. Можно считать, что при вычислении частной производной по какой то переменной остальные переменные рассматриваются просто как константы. Можно также говорить о частных дифференциалах. Полный дифференциал функции многих переменных можно определить как: 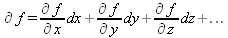 Системы символьной математики позволяют вычислять производные как символьной, так и в численной форме. Выражение (4.1) показывает, что производная f'(x) может быть найдена путем вычисления предела, записанного в (4.1). Этот популярный у математиков метод получил название Δ-метода. В СКМ он используется редко, поскольку они имеют прямые операторы или функции для вычисления производных. 4.3.2. Функции дифференцирования diff и DiffДля вычисления производных Maple имеет следующие основные функции: diff(a, x1, х2, ..., xn) diff(a, [x1, х2, ..., хn]) Diff(a, x1, х2, ..., xn) Diff(a, [x1, х2, ..., xn]) Здесь а — дифференцируемое алгебраическое выражение, в частности, функция f(x1, х2, хn) ряда переменных, по которым производится дифференцирование. Функция Diff является инертной формой вычисляемой функции diff и может использоваться для естественного воспроизведения производных в документах. Первая из этих функций (в вычисляемой и в инертной форме) вычисляет частные производные для выражения а по переменным х1, х2, …, хn. В простейшем случае diff(f(x),x) вычисляет первую производную функции f(x) по переменной х. При n, большем 1, вычисления производных выполняются рекурсивно, например, diff(f(x), х, у) эквивалентно diff(diff(f(x), х), у). Оператор $ можно использовать для вычисления производных высокого порядка. Для этого после имени соответствующей переменной ставится этот оператор и указывается порядок производной. Например, выражение diff(f(x),x$4) вычисляет производную 4-го порядка и эквивалентно записи diff(f(x),x,x,x,x). A diff(g(x,y),x$2,y$3) эквивалентно diff(g(x,y),x,x,y,y,y). Примеры визуализации и вычисления производных (файл diff): > restart; > Diff(a*x^n,x)=diff(а*х^n,х); 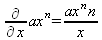 > Diff(a*sin(b*x),x)=diff(a*sin(b*x),x); 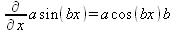 > Diff([sin(x),х^n,ехр(a*x)], x)=diff([sin(x),x^n, exp(a*x)], x); 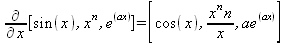 > Diff(а*х^n,x$3)=diff(а*х^n,x$3); 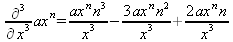 > Diff([х^2,х^3,х^n],x)=diff([х^2,х^3,х^n],x); 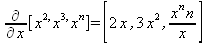 > simplify(%); 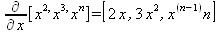 Как видно из приведенных примеров, функции вычисления производных могут использоваться с параметрами, заданными списками. Приведенные ниже примеры показывают эти возможности и иллюстрируют дифференцирование функции пользователя для двух переменных: > restart; > f(х,у):=cos(х)*у^3;f(x,y):=cos(x)y³ > Diff(f(х, y), x) = diff(f(x, y), x); 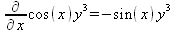 > Diff(f(x, у), y) = diff(f(x, у), y); 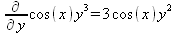 > Diff(f(x,y),x,y)=diff(f(x,у),x,y); 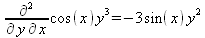 > Diff(f(x,y),x$4)=diff(f(x,y), x$4); 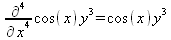 > Diff(f(х,у),y$2)=diff(f(х,у), у$2); 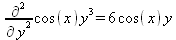 > Diff(f(х,у), х$4,у$4)=diff(f(х,у),х$3,у$2); 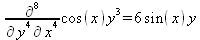 Получаемые в результате дифференцирования выражения могут входить в другие выражения. Можно задавать их как функции пользователя и строить графики производных. 4.3.3. Дифференциальный оператор DДля создания функций с производными может также использоваться дифференциальный оператор D. Порою он позволяет создавать более компактные выражения, чем функции diff и Diff. Дифференциальный оператор можно записывать в следующих формах: D(f) или D[i](f), где параметр f — выражение или имя функции, i — положительное целое число, выражение или последовательность. Оператор D(f) просто вычисляет имя производной от f, поскольку в этой форме он эквивалентен unnaply(diff(f(x),x),x). В форме D(f)(x) этот оператор подобен diff(f(x),x). Приведем примеры дифференцирования функций, заданных только именами, и функций с одним параметром (файл D): > restart; > D(cos^2);-2 sin cos > D(exp^2+cos^2+tan+GAMMA);2exp² - 2sin cos + 1 + tan² + ΨΓ > D(sin)(x)=diff(sin(x), x);cos(x) = cos(x) > D[1](sin*cos);cos² - sin² Следующий пример показывает дифференцирование функции пользователя fun с применением дифференциального оператора D и функции diff: > fun:=(x)->sin(x^2);fun:= x→sin(x²) > D(fun)=diff(fun(x),x);(x→2 cos(x²)x) = 2 cos(x²)x Дифференциальный оператор можно применять и для дифференцирования функций нескольких переменных по заданной переменной (файл D): > f := (х, у, z)->х*ехр(у)+ln(z);f: = (х, у, z) → х еу + ln(z) > D[1](f);(x,y,z) → ey > D[2](f);(x,y,z) → xey > D[3](f);(x,y,z) → ½ Пример применения дифференциального оператора для функции f, заданной программным объектом-процедурой, представлен ниже: > restart; > f:=proc(x,b,n) local i,d,s; > s:=0; > for i from n by -1 to 0 do s:=s*x+b[i] od; > s > end: -> D[1](f); proc(x, b, n) local i, s, sx; sx := 0; s := 0; for i from n by -1 to 0 do sx sx := sx×x + s; s := sx×x + b[i] end do; sx end proc Этот пример показывает реализацию схемы Горнера для полинома b степени n от переменной х. При этом применение оператора дифференцирования возвращает процедуру. Ряд интересных возможностей по вычислению производных предоставляет пакет расширения student. 4.3.4. Импликативное дифференцированиеИногда подлежащая дифференцированию зависимость задана импликативно, т.е. в виде уравнения f. Для дифференцирования таких зависимостей служит функция, используемая в виде: implicitdiff(f,у,х) implicitdiff(f,у,x1,...,xk) Примеры применения импликативного дифференцирования приведены ниже (файл impldiff): > f1 := х*у=1:implicitdiff(f1, у, x); 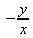 > subs(y=1/x,%); 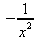 > f2:=2*х^4-3*х^2*у^2+у^4=16:implicitdiff(f2, у, х); 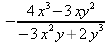 > f3:=x*cos(у)+y*cos(х)=1:implicitdiff(f3,у,x); 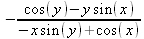 В справке по этой функции можно найти более сложные формы записи этой функции и дополнительные примеры ее применения. 4.3.5. Maplet-вычислитель производных DerivativesПри обучении основам математического анализа удобны обучающие средства на основе Maplet-технологии. Эти новые средства (их не было даже в Maple 9) размещены в позиции Tools меню системы Maple 9.5 при ее применении в стандартном виде. Команда Tools→Tutors Calculus-Single Variables→Derivatives… открывает окно Maple-вычислителя производных, показанное на рис. 4.1. 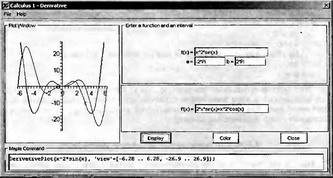 Рис. 4.1 Окно Maplet-вычислителя производных В окне можно в интерактивном режиме задать выражение для функции f(x), вычислить производную f'(x) и, нажав кнопку Dispay, получить графики заданной функции и ее производной в заданных пределах изменения х от а до b. При закрытии окна графики появляются в текущей строке вывода системы Maple 9.5. 4.3.6. Maplet-инструмент по методам дифференцированияПри изучении раздела производных в курсе математического анализа особое значение имеют навыки учащегося в пошаговом дифференцировании выражений в аналитическом виде. В то время, как инженера или научного работника часто удовлетворяет конечное выражение при дифференцировании заданного выражения, учащегося не в меньшей (а порою в куда большей) мере интересуют детали промежуточных вычислений. Такую возможность обеспечивает инструмент Differentiate Methods… по методам аналитического дифференцирования производных. Для открытия его окна надо исполнить команду Tools→Tutors Calculus-Single Variables→Differentiate Methods…. Это окно показано на рис. 4.2. 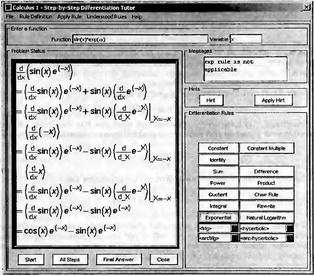 Рис. 4.2. Окно Maplet-инструмента по методам дифференцирования Окно имеет свое меню, область задания функции Function заданной переменной, область вывода функции и результатов ее преобразований и область с кнопками, позволяющими задавать правила дифференцирования и наблюдать результаты их выполнения. Можно задать выполнение всех шагов дифференцирования сразу по всем шагам (кнопка All Steps) или запустить дифференцирование раздельно по шагам (кнопка Start). С помощью кнопки Hint можно вызвать советы по дифференцированию и применить их активизацией кнопки Apply Hint. В поле Differentiate Rules (Правила дифференцирования) имеется множество кнопок, позволяющих применить те или иные правила дифференцирования заданного выражения и опробовать их эффективность. Таким образом имеется возможность выполнить дифференцирование в аналитическом виде различными методами, задаваемыми пользователем. Пример на рис. 4.2 показывает дифференцирование функции f(x)=sin(x)*exp(-х). Представлены шаги дифференцирования и конечный результат. 4.4. Вычисление интегралов4.4.1. Определение интеграловИнтегральное исчисление зародилось из практической необходимости вычисления площадей, объемов и центров тяжести различных фигур. Если есть некоторая функция f(х), то определенный интеграл вида  дает значение площади, ограниченной вертикалями а и именуемыми пределами интегрирования, кривой f(х) и осью абсцисс X. Под площадью надо понимать ее алгебраическое значение, то есть разность между площадью над осью X и под ней. В этом случае ясно, что определенный интеграл может иметь как положительные, так и отрицательные значения. Если f(x)dx есть дифференциал функции F(x), то f(x)dx = dF(x).Функцию F(x) называют первообразной функции f(х). Наиболее общий вид первообразной функции f(x) называют неопределенным интегралом и обозначают как ∫f(x)dx.Соответственно определенный интеграл определяется как:  В состав этого выражения включена некоторая постоянная интегрирования С, подчеркивающая, что для одной и той же f(х) существует масса первообразных, описываемых одной и той же линией, но смещенных по вертикали на произвольную постоянную. Например, для f(х)=sin(x) имеем ∫sin(x)dx = -sin(x) + С.Определенный интеграл представляется числом, а неопределенный — функцией. Для их вычисления используются принципиально различные методы. Так, вычисление неопределенного интеграла возможно только в системах символьной математики. А вот для вычисления определенных интегралов используются как символьные, так и численные методы интегрирования. Встречается ряд специальных видов интегралов. Один из них — интеграл с переменным верхним пределом, представленный в виде:  В данном случае верхний предел представлен функцией y(х). Следует отметить, что Maple обычно стремиться вычислить определенный интеграл в аналитическом виде, даже если он представляется числом. Если нужно найти заведомо численное значение определенного интеграла, можно воспользоваться численными методами вычисления. 4.4.2. Вычисление неопределенных интеграловДля вычисления неопределенных и определенных интегралов Maple предоставляет следующие функции: int(f,x); int(f,х=а..b); int(f,х=а..b,continuous); Int(f,x); Int(f,x=a..b); Int(f,x=a..b,continuous); Здесь f — подынтегральная функция, x — переменная, по которой выполняются вычисления, а и b — нижний и верхний пределы интегрирования, continuous — необязательное дополнительное условие. Maple старается найти аналитическое значение интеграла с заданной подынтегральной функцией. Если это не удается (например, для «не берущихся» интегралов), то возвращается исходная запись интеграла. Ниже приведены примеры визуализации и вычисления неопределенных интегралов (файл intex): > Int(a*x^n,x)=int(а*х^n,х); 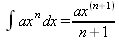 > Int(sin(х)/х,х)=int(sin(х)/х,х); 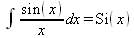 > Int(ln(х)^3,х);∫ln(x)³dx > value(%);ln(x)³x - 3х ln(x)² = 6х ln(x) - 6х > Int(х^5*ехр(-х),х);∫x4e(-x)dx > value(%);-х5 е(-x) - 5х4е(-x) - 20х3е(-x) - 60х2е(-х) - 120хе(-x) - 120е(-x) > Int(1/х,x)=int(1/х,х); 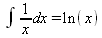 Обратите внимание, что в аналитическом представлении неопределенных интегралов отсутствует произвольная постоянная С. Не следует забывать о ее существовании. Возможно вычисление сумм интегралов и интегралов сумм, а также интегралов от полиномов. > Sum(Int(x^i,х),i=1..5); 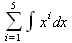 > value(%); 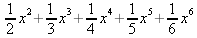 > Int(sum(х^i, i=1..5),x); 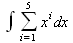 > value(%); 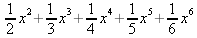 > Р(х):=а*х^3+b*х^2+с*х+d;Р(х) := ax³ + bx² + сх + d > int(Р(х),х); 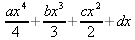 Maple 9.5 успешно берет большинство справочных интегралов. Но не всегда форма представления интеграла совпадает с приведенной в том или ином справочнике. 4.4.3. Конвертирование и преобразование интеграловВ некоторых случаях Maple не может вычислить интеграл. Тогда он просто повторяет его. С помощью функций taylor и convert можно попытаться получить аналитическое решение в виде полинома умеренной степени, что демонстрирует следующий характерный пример: > int(exp(sin(х)),х);∫esin(x)dx > convert(taylor(%,х=0,8),polynom); 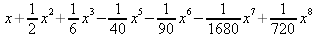 Естественно, что в этом случае решение является приближенным, но оно все же есть и с ним можно работать, например, можно построить график функции, представляющей данный интеграл. Система Maple непрерывно совершенствуется. Например, в Maple V R4 интеграл с подынтегральной функцией ехр(х^4) не брался, а системы Maple, начиная с версии Maple 7, с легкостью берут его: > Int(exp(x^4),х)=int(exp(х^4),х); 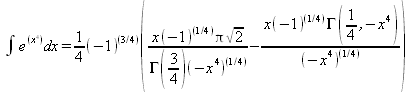 Хотя полученный результат, выраженный через гамма-функцию, нельзя назвать очень простым, но он существует и с ним также можно работать. Например, можно попытаться несколько упростить его, используя функцию simplify: > simplify(%); 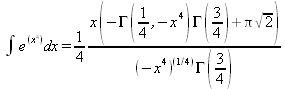 Разумеется, существует также множество иных возможностей и приемов для выполнения операции интегрирования. В дальнейшем мы неоднократно будем рассматривать и другие, более специфические функции для осуществления интегрирования и вычисления интегральных преобразований. В частности, ряд средств вычисления интегралов реализован в пакете student. 4.4.4. Вычисление определенных интеграловДля вычисления определенных интегралов используются те же функции int и Int, в которых надо указать пределы интегрирования, например. х=а..b, если интегрируется функция переменной х. Это поясняется приведенными ниже примерами: > Int(sin(x)/x,х=а..b)=int(sin(х)/х,х=а..b); 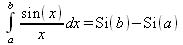 > Int(sin(х)/х,х=0..1.)=int(sin(х)/х, х=0..1.); 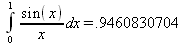 > Int(х*ln(х),х=0..1)=int(x*ln(x), х=0..1); 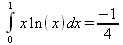 > Int(х*ехр(-х),х=0..infinity)=int(х*ехр(-х), х=0..infinity); 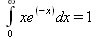 > Int(1/(х^2+6*х+12),x=-infinity..infinity); 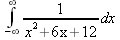 > value(%);⅓π√3 Как видно из этих примеров, среди значений пределов может быть бесконечность, обозначаемая как infinity. 4.4.5. Каверзные интегралы и визуализация результатов интегрированияРассмотрим интеграл, который встречает трудности при вычислении с ограниченным числом верных знаков в процессе вычислений. Maple 8/9/9.5 (кстати, как и Mathematica 4/5), с легкостью берут этот интеграл и позволяют сразу и без какой-либо настройки вычислить для него как точное, так и приближенное значение: > Int(х^20*ехр(-х),х=0..1)=int(х^20*ехр(-х),х=0..1); 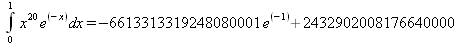 > evalf(%,30);.0183504676972562063261447542317 = .01835046770 Любопытно, что версия Maple 6 при задании погрешности по умолчанию вычисляла значение этого интеграла также как 0, тогда как Maple 9.5 «поумнел» уже настолько, что дает значение 0.01835046770 даже в этом, не очень удачном, случае. Более того Maple 9/9.5 позволяет наглядно проиллюстрировать характер промежуточных вычислений подобных интегралов: > int(х^20*ехр(-х),х);½+½I√3, ½-½I√3, RootOf(_Z5 + _Z4 - _Z2 - _Z - 1, index = 1), RoolOf(_Z5 + _Z4 - _Z2 - _Z - 1, index = 2), RootOf(_Z5 + _Z4 – _Z2 - _Z - 1, index = 3), RootOf(_Z5 + _Z4 - _Z2 - _Z - 1, index = 4), RootOf(_Z5 + _Z4 - _Z2 - _Z - 1, index = 5) Нетрудно заметить, что решение распадается на множество слагаемых, соответствующих общеизвестному интегрированию по частям. В каждом слагаемом имеются большие числа и потому принципиально необходимо применение арифметики высокой точности (или разрядности). Maple 9/9.5 такими средствами, причем превосходными, обладает. Продолжим изучение данного «каверзного» интеграла. Опробуем силы Maple на интеграле более общего вида, где конкретный показатель степени заменен на обобщенный — n. Здесь нас ожидает приятный сюрприз — Maple с легкостью выдает аналитическое решение для данного определенного интеграла: > у:=(n)->int(х^n*ехр(-х),х=0..1); 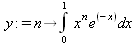 > y(n); 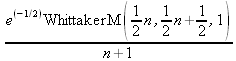 > y(20);-6613313319248080001 e(-1)+ 2432902008176640000 > evalf(%,30);.01835046770 > у(20.);0. Однако радоваться несколько преждевременно. Многие ли знают, что это за специальная функция — WhittakerM? Но хуже другое — Maple при конкретном n=20 дает грубо неверное решение — 0 (почему — уже объяснялось). Забавно, что при этом сама по себе функция WhittakerM вычисляется для n=20 без проблем: > WhittakerM(10,10.5,1);.6353509348 А теперь присмотритесь к новому результату вычисления злополучного интеграла. Оказывается, он уже не содержит больших чисел, свойственных прямому решению! Зная значение WhittakerM с погрешностью по умолчанию, можно уверенно вычислить приближенное численное значение интеграла с той же погрешностью, уже не прибегая к арифметике высокой точности: > (ехр(-.5)*WhittakerM(10,10.5,1))/21;.01835046770 На рис. 4.3 приведен график зависимости значений данного интеграла от показателя степени n при его изменении от 0 до 50. Плавный ход графика показывает, что в вычислении данного интеграла нет никаких признаков неустойчивости решения при изменении n, если соблюдать правило выбора достаточно малой погрешности вычислений. 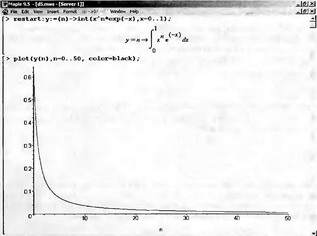 Рис. 4.3. Значение интеграла от х^nехр(-х) как функция n Наличие у функции особых (сингулярных) точек нередко затрудняет выполнение с ней ряда операций, таких как численное интегрирование. В этом случае могут помочь соответствующие параметры. Например, вычисление в Maple 8/9 следующего интеграла дает явно неудобное выражение в виде набора значений, разных для разных интервалов изменения a: > int(1/(х+а)^2,х=0..2); 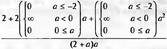 Этот интеграл расходится, поскольку при x=-a подынтегральная функция устремляется в бесконечность, что и показывает приведенное выражение. График зависимости значения интеграла от параметра а имеет подозрительный вид. Это как раз тот случай, когда надо обратить особое внимание на результаты полученные системой Maple. А теперь покажем, как выглядит этот пример при его решении в системе Maple 9.5 — рис. 4.4. Обратите внимание на «провал» графика в средней части. 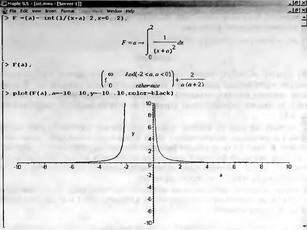 Рис. 4.4. Построение графика зависимости значений интеграла с подынтегральной функцией 1/(х+а)^2 от параметра a Интересно, что если в нашем случае, применить параметр continuous (в апострофах) при вычислении интеграла, можно получить более простое выражение: > int(1/(х+а)^2,х=0..2,`continuous`); 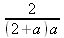 Рис. 4.5 показывает это решение с двумя важными дополнениями — оно представляется функцией пользователя, а ее график строится при изменении а от -10 до 10. «Провал» в средней части графика уже отсутствует. 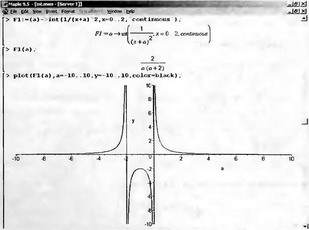 Рис. 4.5. Зависимость значения интеграла с подынтегральной функцией 1/(х+а)^2 и пределами от 0 до 2 от параметра а Приведем еще один пример «каверзного» интеграла довольно простого вида: > int(1/х^3,х=-1..2);undefined Этот интеграл не берется вообще, так что Maple совершенно справедливо об этом и сообщает. Но введение параметра CauchyPrincipalValue позволяет получить численное значение интеграла: > int(1/х^3,х=-1..2,`CauchyPrincipalValue`);⅜ Возьмем еще один наглядный пример — вычисление интеграла от синусоидальной функции при произвольно больших пределах, но кратных 2π! Очевидно, что при этом (учитывая равность площадей положительной и отрицательной полуволн синусоиды) значение интеграла будет равно 0. Например: > int(sin(х),x=-1000*pi..1000*pi);0 Однако распространение этого правила на бесконечные пределы интегрирования является грубейшей ошибкой. Интеграл такого рода уже не сходится и Maple дает соответствующий результат: > int(sin(х),x=-infinity..infinity);undefined Во многих областях техники часто употребляются математически неточные выражения «затухающая синусоида» или «нарастающая синусоида». Возьмем, к примеру, широко распространенную функцию: у(t)=exp(-t)sin(2π). Построим ее график и вычислим определенный интеграл от этой функции с пределами от 0 до ∞ (рис. 4.6). 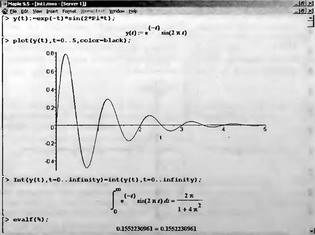 Рис. 4.6. График «затухающей синусоиды» и интеграл от нее с пределами от 0 до ∞ С первого взгляда на график видно, что каждая положительная полуволна функции (затухающей «синусоиды») явно больше последующей отрицательной полуволны. К тому же осцилляции функции быстро затухают и через десяток-другой периодов значение функции становится исчезающе малым. Вот почему Maple уверенно вычисляет интеграл с такой подынтегральной функцией. Ее свойство — неопределенность при t→∞ просто исчезает. А теперь возьмем антипод этой функции — «синусоиду с экспоненциально нарастающей до стационарного значения 1 амплитудой». Такая функция записывается следующим образом: Y(t) = (1 - ехр(-t)) sin(2πt).Ее график и попытки вычисления интеграла с такой подынтегральной функцией приведены на рис. 4.7. 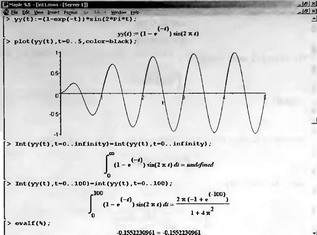 Рис. 4.7. График «экспоненциально нарастающей синусоиды» и интеграл от нее с пределами от 0 до ∞ Обратите внимание на то, что здесь прямое вычисление интеграла к успеху не привело, хотя из графика функции видно, что каждая положительная полуволна в близкой к t=0 области явно больше по амплитуде, чем последующая отрицательная полуволна. Однако, в отличие от предыдущей функции, при больших значениях аргумента данная функция вырождается в обычную синусоиду с неизменной (и равной 1) амплитудой. Вот почему Maple честно отказывается вычислять не сходящийся интеграл от такой «коварной» функции. 4.4.6. Вычисление несобственных интегралов первого родаНесобственными интегралами называют интегралы, у которых хотя бы один из пределов или подынтегральная функция устремляются в бесконечность. Соответственно различают несобственные интегралы первого и второго родов. Вычисления таких интегралов требует повышенного внимания и порой использования специальных методов. Из-за этого в старых реализациях Maple нередко такие интегралы просто не вычислялись, хотя на самом деле их решения (порою в виде специальных функций) существовали. Последние версии Maple существенно продвинулись в направлении решения многих несобственных интегралов. Это видно из благополучного решения ряда таких несобственных интегралов первого рода, о которых спотыкались старые версии Maple и которые требуют специальных решений (файл intspec): > Int(sin(х)/х^2,х=1..infinity); 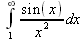 > value(%);evalf(%);sin(1) - Ci(1) 0.5040670619 > Int(sin(x)^2,х=0..infinity); 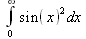 > value(%);∞ > Int(exp(-t^2)*sin(t^2),t=0..infinity); 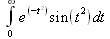 > value(%);evalf(%); 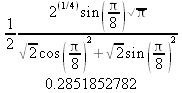 > r:=Int(cos(x)/sqrt(х+х^2),x=0..infinity); 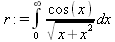 > value(r);evalf(r11); 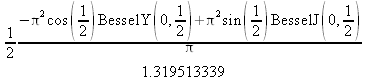 > Int(ехр(-t^2), t=-infinity..infinity); 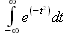 > value(%);√π > Int(exp(-t^2)*t*2, t=-infinity..infinity); 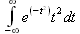 > value(%); 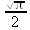 > Int(exp(-t)/t^(1/3), t=0..infinity); 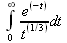 > value(%); 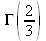 > Int(exp(-t)*ln(t),t=0..infinity); 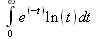 > value(%);-γ > Int(exp(-t)*ln(t)/t=1..infinity); 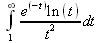 > value(%);  > evalf(%);0.0506523094 > Int(exp(-x)*cos(x),x=0..infinity); 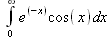 > value(%);½ Для подавляющего большинства интегралов результат вычислений с применением функций Int и int оказывается абсолютно идентичным. Однако есть и исключения из этого правила. Например, следующий интеграл благополучно очень быстро вычисляется функцией Int с последующей evalf: > Int(cos(х)/(x^4+x+1),x=-infinity..infinity); 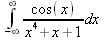 > evalf(%);1.878983562 Однако в Maple 9 функция int вместо числа возвращает «страшное» выражение: > int(cos(х)/(х^4+х+1),x=-infinity..infinity); 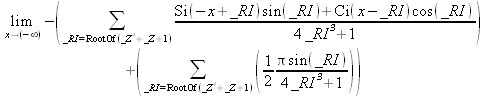 Увы, но функция evalf(%), примененная после него, к более простому выражению не приводит — она просто повторяет выражение в выходной строке. Maple 9.5 при вычислении этого интеграла просто «завис» и спустя минуту так и не выдал результат. Построив график подынтегрального выражения (проделайте это сами) можно убедиться в том, он представляет собой сильно затухающую волну с узким высоким пиком в точке x=1. Попытаемся выполнить интегрирование в достаточно больших, но конечных пределах, где волна почти полностью затухает: > int(cos(х)/(х^4+х+1),х=-1000..1000); 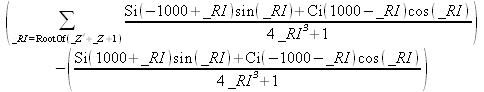 > evalf(%);1.878983561 +0.I На сей раз результат получен (Maple 9.5 затратил на это около секунды). Он очень близок к полученному функцией Int, но все же имеет подозрительную мнимую часть с вроде бы нулевым значением. Он показывает, что не все здесь благополучно и что «пенки» в вычислении некоторых интегралов в Maple 9.5 все же возможны. 4.4.7. Вычисление несобственных интегралов второго родаК несобственным интегралам второго рода относятся интегралы, имеющие в пределах интегрирования особенности подынтегральной функции. При этом сами пределы могут быть и конечными. Некоторые интегралы не имеют в среде Maple 9.5 общего решения, но исправно вычисляются для частных случаев (см. ниже для n неопределенного и конкретного n=6): > Int(1/sqrt(1-х^n),х=0..1); 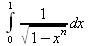 > value(%); Definite integration: Can't determine if the integral is convergent. Need to know the sign of —> n Will now try indefinite integration and then take limits. 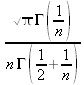 > Int(1/sqrt(1-х^6),х=0..1)=evalf(int(1/sqrt(1-х^6) , х=0..1)); 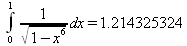 Приведем тройку примеров, требующих для вычислений «вручную» заметных умственных усилий, но прекрасно выполняемых системой Maple: > Int((х-1)/ln(х),х=0..1)=int((х-1)/ln(х),х=0..1); 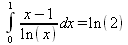 > Int(ln(1-х)/x,x=0..1)=int(ln(1-х)/x,x=0..1); 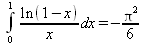 > Int(exp(-x)*sin(x)/x,x=0..infinity)=int(exp(-x)*sin(x)/x, x=0..infinity); 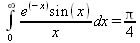 Однако не стоит думать, что всегда «коту масленица». Следующий интеграл дает весьма подозрительный результат: > Int(1/(х^2*(sqrt(х^2-9))),х=0..infinity); 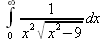 > value(%);–∞I Это наглядный пример, когда Maple 9.5 «нагло врет», несмотря на заверения его создателей о том, что эта система прошла полную сертификацию на вычисления интегралов. Выполнив некоторые преобразования, найдем интеграл в системе Maple 8: > Int(1/(t^2*(sqrt(t^2-9))), t=3..x) = int(1/(t^2*(sqrt(t^2-9))), t=3..x); 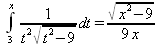 Увы, Maple 9.5 вычислять данный интеграл не желает — он его просто повторяет. Но, и в Maple 8 и в Maple 9.5 нужное значение определяется пределом этого выражения при х, стремящемся к бесконечности: > Int(1/(x^2*(sqrt(х^2-9))),х=0..infinity) = value(Limit(rhs(%),x=infinity)); 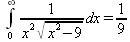 Этот пример наглядно показывает, что иногда полезны аналитические преобразования, выполняемые «вручную», то бишь с помощью своей головы. К сожалению, с подобными «фокусами» иногда приходится встречаться. Приведенные примеры говорят о том, что и новые реализации Maple не лишены отдельных недостатков, возможно и привнесенных в их доработанное ядро. В общем, как говорят у нас в армии «Доверяй, но — проверяй!». Интегралы, представляемые через специальные математические функции, Maple 9.5/10 нередко вычисляет хуже, чем система Mathematica 4.5/5. 4.4.8. Интегралы с переменными пределами интегрированияК интересному классу интегралов относятся определенные интегралы с переменными пределами интегрирования. Если обычный определенный интеграл представлен числом (или площадью в геометрической интерпретации), то интегралы с переменными пределами являются функциями этих пределов. На рис. 4.8 показано два примера задания простых определенных интегралов с переменным верхним пределом (сверху) и обоими пределами интегрирования (снизу).  Рис. 4.8. Примеры интегралов с переменными пределами интегрирования На этом рисунке построены также графики подынтегральной функции (это наклонная прямая) и функции, которую задаёт интеграл. 4.4.9. Вычисление кратных интеграловФункции int и Int могут использоваться для вычисления кратных интегралов, например, двойных и тройных. Для этого функции записываются многократно (файл intm): > restart; > Int(int(1/(x*y),x=4.0..4.4),y=2.0..2.6);  > value(%);.02500598527 > Int(Int(Int((х^2+у^2)*z, x=0..a), y=0..a), z=0..a);  > value(%);  > Int(Int(2-х-у, x=sqrt(у)..у^2), у=0..1); 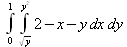 > value(%); 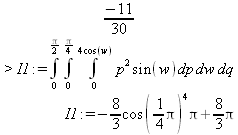 > evalf(I1);-2.666666667 cos(.2500000000 π)4 + 2.666666667 π Обратите внимание на нечеткую работу функции evalf в последнем примере. Эта функция уверенно выдает значение evalf(Pi) в форме вещественного числа с плавающей точкой, но отказывается вычислить значение интеграла, в которое входит число Pi. Этот пример говорит о том, что отдельные недостатки у Maple все же есть, как и поводы для ее дальнейшего совершенствования. В пакете расширения student имеются дополнительные функции интегрирования, которые дополняют уже описанные возможности. В частности, в этом пакете есть функции для вычисления двойных и тройных интегралов. 4.4.10. О вычислении некоторых других интеграловMaple открывает большие возможности в вычислении криволинейных, поверхностных и объемных интегралов. Нередко такие интегралы довольно просто заменяются на интегралы с переменными пределами интегрирования, что и иллюстрируют приведенные ниже примеры. Пусть требуется вычислить объем фигуры, ограниченной координатными плоскостями и плоскостью х+у+z=1. Он, с учетом равенства z=1-х-у, задается интегралом: 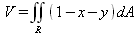 который заменяется следующим интегралом: > Int(Int(1-х-у,у=0..1-х),х=0..1)=int(int(1-х-у,у=0..1-х),х=0..1); 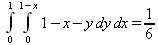 Последний, как видно, легко вычисляется. Теперь вычислим массу указанной фигуры, которая задается тройным интегралом: 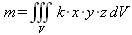 Здесь k — константа, характеризующая удельную площадь вещества. Этот интеграл также сводится к легко решаемому в Maple 9.5: > m=Int(Int(Int(k*x*y*z,z=0..1-x-y),y=0..1-х),x=0..1); 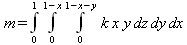 > value(%); 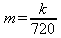 Специальные средства для вычисления подобных интегралов имеет пакет расширения VectorCalculus, который описывается в конце этой главы. 4.4.11. Maplet-демонстрация построения графика первообразнойВ составе самоучителей Maple 9.5 есть раздел Antiderivative, который иллюстрирует технику построения первообразной функции при интегрировании. Для доступа к окну этого инструмента (рис. 4.9) достаточно исполнить команду Tools→Tutors→Calculus-Single Variables→Antiderivative…. 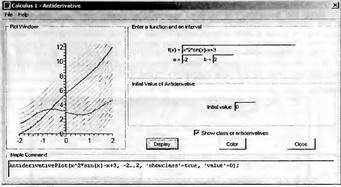 Рис. 4.9. Окно Maplet-демонстрации графиков функций и первообразных Окно Maplet-демонстрэции интегрирования позволяет задать подынтегральную функцию и построить ее график и график первообразной функции, представляющей неопределенный интеграл. В окне а и b это не пределы интегрирования, а пределы изменения х при построении графиков. Опция Show class of antiderivatives позволяет построить графики множества первообразных, с выделением графика первообразной функции для заданного начального значения Initial Value. По завершении работы с окном демонстрации графики выводятся в документ Maple 9.5 — рис. 4.10. 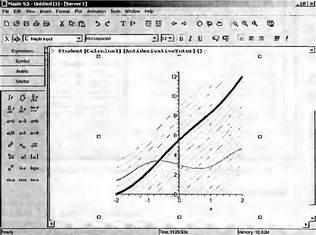 Рис. 4.10. Графики исходной функции и первообразных в окне документа Maple 9 5 4.4.12. Maplet-демонстрация методов интегрированияДля демонстрации методов пошагового интегрирования имеется Maplet-инст-румент Step-by-step Integration Tutor. Для вызова его окна (рис. 4.11) нужно исполнить команду (в стандартном варианте интерфейса): Tools→Tutors→Calculus-Single Variables→Antiderivative…. 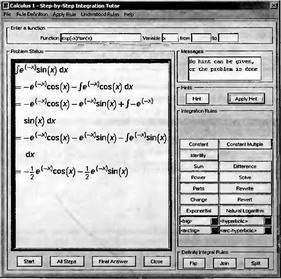 Рис. 4.11. Окно Maplet-демонстрации методов пошагового интегрирования Нетрудно заметить, что это окно практически аналогично окну для демонстрации методов пошагового дифференцирования, описанному в разделе 4.3.4 (рис. 4.2). В связи с этим подробное описание средств этого инструмента можно опустить. Отметим лишь, что он позволяет задавать подынтегральную функцию и пределы интегрирования и по шагам (автоматически или вручную) вычислять интегралы. По окончании работы с окном соответствующий интеграл и результат его вычисления появляется в окне документа — рис. 4.12. 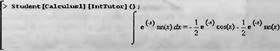 Рис. 4.12. Пример вывода результата работы с Maplet-инструментом по методам интегрирования 4.4.13. Численное вычисление определенных интеграловДля численного вычисления определенных интегралов используется функция evalf в сочетании с функциями Int или int: evalf(Int(f, x=a..b, …)) evalf(Int(f, a..b, …)) evalf(Int(f, list-of-equations, …)) evalf(Int(f, list-of-ranges, …)) evalf(int(f, x=a..b)) Вместо многоточия могут использоваться различные опции, например, для задания метода вычислений. Могут использоваться комбинированные методы (аналитический с численным), ряд Maple-методов повышенной точности, методы предложенные группой NAG, метод Монте-Карло и др. Детали задания методов можно найти в справке. Ограничимся несколькими примерами вычисления определенных интегралов в численном виде (файл intnum): > Int(х^2,х=1..2)=evalf(Int(х^2,х=1..2)); 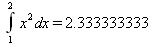 > Int(sin(x)/x,х=0..Pi)=evalf(int(sin(х)/х,х=0..Pi)); 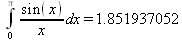 > Digits:=15;Int(sin(x)/x,x=0..Pi)=evalf(int(sin(x)/x, x=0..Pi, method = _NCrule));Digits := 15 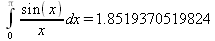 > expr := x*exp(-x): Int(expr, x=1..infinity) = evalf[40](Int(expr, x=1..infinity, method=_Gquad)); 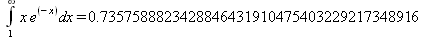 В двух последних примерах показано вычисление интегралов с повышенной точностью в 15 и 40 верных знаков. Аналогичным образом могут вычисляться и кратные интегралы. На время и возможность вычисления определенных интегралов большое значение оказывает выбранный метод вычислений. Нередко его стоит указывать явно. Ниже приведены примеры этого с оценкой времени интегрирования (файл intmet): > restart: t:=time(): int((1-ехр(-z^2))/(BesselJ(1, z)^2+ BesselY(1,z)^2)/z^3,z=0.0..infinity); time()-t;1.979213867 72.375 > t:=time(): evalf(Int((1-ехр(-z^2))/(BesselJ(1, z)^2+ BesselY(1,z)^2)/z^3,z=0..infinity, Gquad)); time()-t;1.979213867 2.579 > t: =time(): evalf(Int((1-exp(-z^2))/(BesselJ(1, z)^2+ BesselY(1,z)^)/z^3,z=0.. infinity,_CCquad)); time()-t;1.979213867 2.578 > t:=time(): evalf(Int((1-ехр(-z^2))/(BesselJ(1,z)^2+ BesselY(1,z)^2)/z^3,z=0..infinity,_Sinc)); time()-t;1.979213867 3.876 > t:=time(): evalf(Int((1-ехр(-z^2))/(BesselJ(1, z)^2+ BesselY(1,z)^2)z^3,z=0..infinity,_Dexp)); time()-t;1.979213867 1.531 В данном случае лучшим оказался метод _Dexp (адаптивный двойной экспоненциальный метода). Разумеется, для других интегралов более целесообразным может оказаться применение другого метода. Приведенные значения времен интегрирования могут заметно отличаться при реализации вычислений на разных ПК. Данные выше приведены для ПК с процессором Pentium 4 НТ с рабочей частотой 2,6 ГГц. 4.5. Вычисление пределов функций4.5.1. Определение предела функцииПределом функции f(х) называют то ее значение b, к которому функция неограниченно приближается в точке х=а (предел в точке) или слева или справа от нее. Пределы обозначается как:
При этом подразумевается, что функция f(x) определена на некотором промежутке, включающем точку х=а и во всех точках, близких к ней слева и справа. В последнем случае предел вычисляется для х=а-h или x=a+h при h стремящемся к нулю. Пределом может быть число, математическое выражение и положительная или отрицательная бесконечность. Последнее соответствует расширенному представлению о пределах. 4.5.2. Функции вычисления пределов в Maple 9.5Для вычисления пределов функции f в точке х=а используются следующие функции: limit(f,x=a); limit(f,x=a,dir); Limit(f,x=a); Limit(f,x=a,dir); Здесь f — алгебраическое выражение, z — имя переменной, dir — параметр, указывающий на направление поиска предела (left — слева, right — справа, real — в области вещественных значений, complex — в области комплексных значений). Значением а может быть бесконечность (как положительная, так и отрицательная). Примеры применения этих функций для вычисления пределов в точке приведены ниже (файл limit): > restart: Limit(f(х),х=а); 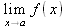 > Limit(1-ехр(-х), x=infinity)=limit(1-exp(-x), x=infinity); 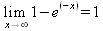 > Limit(exp(x),x=infinity) = limit(exp(x),x=infinity); 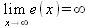 > Limit(exp(-x),x=infinity)=limit(exp(-x),x=infinity); 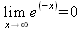 > Limit((x-sin(x))/x^3, x=0)=limit((x-sin(x))/х^3,х=0); 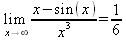 > Limit((Pi-2*x)*tan(x),x=Pi/2)=limit(tan(x)*(Pi-2*x), x=Pi/2); 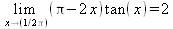 Обратите внимание на то, что в первом примере фактически дано обозначение предела в самом общем виде. Приведем еще пример вычисления предела функции в виде дроби, имеющей неопределенность 0/0: > Limit((x-sin(х)) / (exp(2*х)-1-2*х-2*х^2),x=0) = limit((х-sin(x))/(exp(2*х)-1-2*х-2*х^2),х=0); 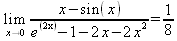 Как видно из этого примера, Maple «понимает» особенности функций при вычислении пределов. 4.5.3. Вычисление пяти замечательных пределовПроверим возможности Maple при вычислении пяти замечательных пределов (файл limit5 — второй предел дан в двух вариантах): > Limit(sin(х)/х,х=0)=limit(sin(х)/х,х=0); 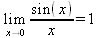 > Limit((1+х)^(1/х),х=0)=limit((1+х)^(1/х),х=0); 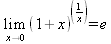 > Limit((1+1/х)^х,x=infinity)=limit((1+1/х)^х,x=infinity); 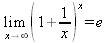 > Limit(ln(1+x)/х,x=0)=limit(ln(1+х)/x,x=0); 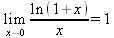 > Limit((exp(х)-1)/х,х=0)=limit((exp(х)-1)/х,х=0); 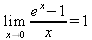 > Limit(((1+х)^а-1)/х,х=0)=limit(((1+х)^а-1)/х,х=0); 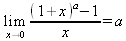 Все пять замечательных пределов вычислены верно. 4.5.4. Графическая иллюстрация вычисления пределов с двух сторонРисунок 4.13 показывает вычисление пределов функции tan(x) в точке x=π/2, а также слева и справа от нее. Для указания направления используются опции right (справа) и left (слева). Видно, что в самой точке предел не определен (значение undefined), а пределы справа и слева уходят в бесконечность. 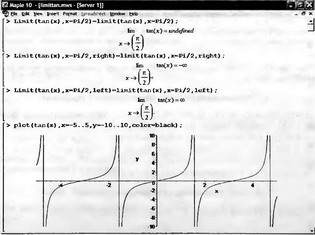 Рис. 4.13 Пример вычисления пределов функции tan(x) и построение ее графика Показанный на рис. 4.13 график функции tan(x) наглядно подтверждает существование пределов справа и слева от точки x=π/2 и отсутствие его в самой этой точке, где функция испытывает разрыв от значения +∞ до -∞. 4.5.5. Maplet-инструмент для иллюстрации методов вычисления пределовДля демонстрации методов пошагового вычисления пределов имеется Maplet-инструмент Step-by-step Limit Tutor. Для вызова его окна (рис. 4.14) нужно исполнить команду (в стандартном варианте интерфейса): Tools→Tutors→Calculus-Single Variables→Limit…. 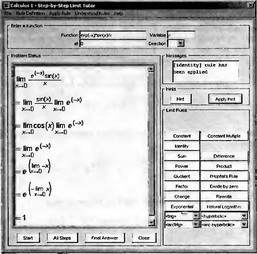 Рис. 4.14. Окно Maplet-демонстрации методов пошагового вычисления пределов Нетрудно заметить, что это окно практически аналогично окну для демонстрации методов пошагового дифференцирования, описанному в разделе 4.3.4 (рис. 4.2). В связи с этим подробное описание средств и этого инструмента можно опустить. Отметим лишь, что он позволяет задавать функцию и значение x и по шагам (автоматически или вручную) вычислять пределы. По окончании работы с окном соответствующий предел и результат его вычисления появляется в окне документа — рис. 4.15.  Рис. 4.15. Пример вывода результата работы с Maplet-инструментом по методам вычисления пределов 4.6. Разложение функций в ряды4.6.1 Определение рядов Тейлора и МаклоренаОгромное разнообразие функций давно заставляло математиков задумываться над возможностями их приближенного, но единообразного представления. К таким представлениям относятся различные ряды, сходящиеся к значениям функций в окрестности заданной точки. Очень часто желательно представление тех или иных функций f(х) в достаточно простом и единообразном виде. Эта задача решается методами аппроксимации, которые мы рассмотрим позже. Пока же зададимся более простой задачей — представления функций в виде степенного многочлена F(x) в окрестности заданной на оси абсцисс точки х=х0. Такое разложение было впервые получено Тейлором и получило название ряда Тейлора [68, 69]: 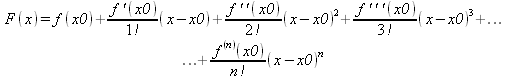 Если разложение выполняется относительно точки х=0, его принято называть рядом Маклорена: 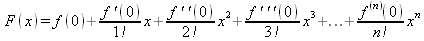 4.6.2. Разложение в степенной рядДля разложения функции или выражения expr в обычный степенной ряд в системе Maple служат функции: series(expr, eqn) и series(expr, eqn, n) Здесь expr — разлагаемое выражение, eqn — условие (например, в виде х=а) или имя переменной (например, х) и n — необязательное и неотрицательное целое число, задающее число членов ряда (при его отсутствии оно по умолчанию берется равным 6, но может переустанавливаться системной переменной Order). Если в качестве eqn задано имя переменной, то это соответствует разложению по этой переменной в области точки с ее нулевым значением. Задав eqn в виде x=x0 можно получить разложение по переменной х в окрестности точки x=х0. Разложение получается в форме степенного многочлена, коэффициенты которого задаются рациональными числами. Остаточная погрешность задается членом вида O(х)^n. При точном разложении этот член отсутствует. В общем случае для его удаления можно использовать функцию convert. Ниже представлены примеры разложения различных выражений в ряд (файл series): > series(sinh(х), х=0); 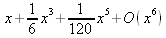 > series(sinh(х),х=1,3); 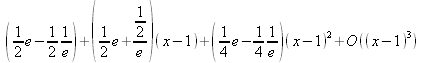 > series(sinh(х),х=1.0,3);1.175201193 + 1.543080635(х-1.0) + .5876005967(х-1.0)² + O((х-1.0)³) > series(2*х^2-х+1,х=1,10);2 +3(x - 1) +2(х - 1)² > f(х):=sin(х)/х; 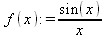 > series(f(х),х=0,10); 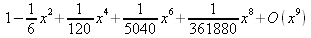 > convert(%,polynom); 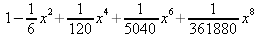 > s:=series(ln(х),х=2, 4); 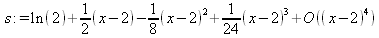 > evalf(convert(s,polynom));-.3068528194 + .5000000000x - .1250000000(x-2.)² + .04166666667(x-2.)³ Здесь видно, что член, обозначающий погрешность, отсутствует в тех разложениях, которые точны — например, в разложениях степенных многочленов. 4.6.3. Разложение в ряды Тейлора и МаклоренаДля разложения в ряд Тейлора используется функция taylor(expr, eq/nm, n). Здесь expr — разлагаемое в ряд выражение, eq/nm — равенство (в виде х=а) или имя переменной (например, х), n — необязательный параметр, указывающий на порядок разложения и представленный целым положительным числом (при отсутствии указания порядка он по умолчанию принимается равным 6). При задании eq/nm в виде x=a разложение производится относительно точки x=a. При указании eq/nm в виде просто имени переменной разложение ищется в окрестности нулевой точки, то есть фактически вычисляется ряд Маклорена. Ниже представлены примеры применения функции taylor (файл taylor): > taylor(1-ехр(х), х=1, 4); 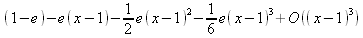 > convert(%,polynom); 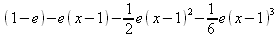 > taylor(sinh(x), x, 10); 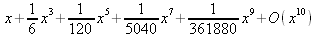 > taylor(int(sin(x)/x,x),x); 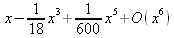 > taylor(erf(х),х); 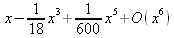 Не все выражения (функции) имеют разложение в ряд Тейлора. Ниже дан пример такого рода: > taylor(1/х+х^2,х,5); Error, does not have a taylor expansion, try series() > series(1/х+х^2,x,10);x-1 + x2 > taylor(1/х+х^2,x=1,5);2 + x-1 + 2(x-1)2 - (x-1)3 + (x-1)4 +O((x-1)5) Здесь Maple 9.5 отказался от вычисления ряда Тейлора в окрестности точки х=0 (по умолчанию) и предложил воспользоваться функцией series. Однако эта функция просто повторяет исходное разложение. В то же время в окрестности точки х=1 ряд Тейлора вычисляется. Для разложения в ряд Тейлора функций нескольких переменных используется библиотечная функция mtaylor: mtaylor(f, v) mtaylor(f, v, n) mtaylor(f, v, n, w) Здесь f — алгебраическое выражение, v — список имен или равенств, n — необязательное число, задающее порядок разложения, w — необязательный список целых чисел, задающих «вес» каждой из переменных списка v. Эта функция должна вызываться из библиотеки Maple 9 с помощью команды readlib: > readlib(mtaylor); mtaylor(sin(х*у),[х,у],10,[2,1]);proc() ... end proc x y - ⅙ x³ y³ > mtaylor(exp(-x)*sin(y),[x,y],5); 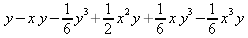 Для получения только коэффициента при k-м члене ряда Тейлора можно использовать функцию coeftayl(expr,var,k). Если expr — функция нескольких переменных, то k должен задаваться списком порядков коэффициентов. 4.6.4. Пример документа — разложения синуса в рядПолезно сочетать разложение выражений (функций) в ряд Тейлора с графической визуализацией такого разложения. Рассмотрим документ, в котором наглядно показаны возможности представления функции рядами Тейлора и Маклорена. На рис. 4.16 показана первая часть документа. Она дает пример разложения в ряд Тейлора функции sin(x) с построением ее графика и графика по разложению в ряд. 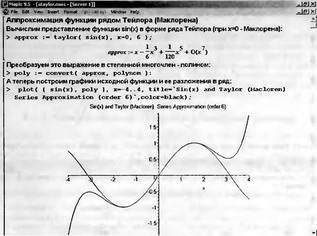 Рис. 4.16. Разложение функции sin(x) в ряд Маклорена шестого порядка и построение ее графика Поскольку выбрано разложение относительно точки х=0, то полученный ряд является рядом Маклорена. Это хороший пример визуализации результатов математических вычислений — здесь наглядно видно, что при малых значениях x график ряда практически повторяет разлагаемую функцию, но затем начинает сильно от нее отходить. Обратите внимание на следующее — несмотря на то, что мы задали шестой порядок ряда, последний член имеет только пятый порядок. Это связано со спецификой данного разложения — в нем просто отсутствуют члены четного порядка. Можно буквально в считанные секунды попробовать изменить число членов ряда или диапазон изменения переменной х, что и показано на рис. 4.17 (вторая часть документа). При этом легко убедиться в том, что при больших x поведение ряда не имеет ничего общего с поведением разлагаемой в ряд функции — в частности, нет и намека на периодичность разложения, которая присуща тригонометрической функции sin(x). 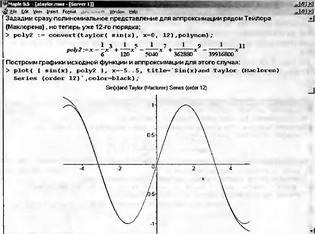 Рис. 4.17. Разложение функции sin(x) в ряд Маклорена 12-го порядка и построение ее графика В заключительной (третьей) части этого документа (рис. 4.18) представлено уже истинное разложение синуса в ряд Тейлора в окрестности смешенной от нуля точки х=1. При смещении точки, относительно которой ведется разложение, выражение для ряда Тейлора существенно изменяется. В нем, во-первых, появляются члены четных степеней, а во-вторых, фигурирует аргумент вида (х-1)n. 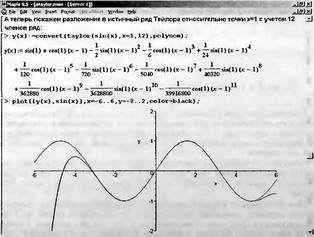 Рис. 4.18. Разложение функции sin(x) в ряд Тейлора 12-го порядка относительно точки x=1 и построение ее графика Нетрудно заметить, что даже при представлении такой «простой» функции, как sin(x), приемлемая погрешность представления одного периода достигается при числе членов ряда Тейлора порядка 10 и более. Однако существенное повышение порядка ряда нецелесообразно из-за резкого возрастания вычислительных погрешностей. Впрочем, если задать достаточно большое число верных цифр результатов, то в Maple можно использовать ряды с гораздо большим числом членов. Кроме того, серьезным недостатком аппроксимации рядом Тейлора является непредсказуемое поведение полинома вдали от точки, относительно которой задается представление. Это хорошо видно на всех трех приведенных примерах. Помимо указанных выше разложений в ряд Maple имеет множество функций для иных разложений. Например, в пакете numapprox имеется функция laurent(expr,var,n), позволяющая получить разложение в ряд Лорана, функция chebyshev(expr, eq/nm, eps) дает разложение в форме полиномов Чебышева и т.д. 4.6.5. Пакет вычисление степенных разложений powseriesСтепенные разложения часто используются в математических расчетах для приближенного представления разнообразных функций и обеспечения единообразия такого представления. В пакете powseries сосредоточены расширенные средства по реализации таких разложений. Пакет загружается командой: > with(powseries): Ниже представлено определение функций этого пакета: compose(a.b) — объединяет ряды а и b; evalpow(expr) — вычисляет выражение expr и возвращает его в виде ряда; inverse(p) — инвертирует ряд р; multconst(p,const) — умножает ряд p на константу const; multiply(a,b) — умножает ряд а на ряд b; negative(p) — возвращает аддитивный обратный по отношению к р ряд; powadd(a,b,…) — складывает ряды а, b, …; powcreate(expr) — создает ряд для выражения expr; powpoly(pol,var) — создает ряд для полинома pol по переменной var; powsolve(sys) — создает ряд для решения дифференциальных уравнений sys; quotient(a.b) — возвращает частное для а и b в виде ряда; reversion(a) — дает обратное к композиции разложение ряда а; subtract(a.b) — дает разность рядов а и b. В выражении expr могут использоваться операторы +, -, *, / и ^. С ними могут комбинироваться встроенные функции и функции пользователя, например fig). Кроме того, могут использоваться следующие функции: Powexp powinv powlog povmeg powrev Powdiff powint powquo powsub powcos Powtan powsec powcsc powcot powsinh Powcosh powtanh powsech powcsch powcoth Powsqrt powadd multiply 4.6.6. Примеры выполнения степенных разложенийНазначение большинства этих функций очевидно из их названий — они возвращают соответствующую функцию (указанную после слова pow в имени) в виде разложения в ряд или полинома. Например, powexp раскладывает выражения с экспоненциальными функциями в ряд. Получаемые функциями ряды представляются в специальном формате. Поэтому для их применения в обычном виде необходимо использовать функцию tpsform в следующих видах: tpsform(p, var, order) — преобразует ряд p в обычную форму с заданием порядка order; tpsform(p, var) — преобразует ряд p в обычную форму с порядком, заданным переменной Order. Здесь p — имя степенного ряда, var — переменная, относительно которой записан ряд, order — порядок ряда. Если параметр order не указан, используется значение глобальной переменной Order. Ниже даны примеры, иллюстрирующие технику работы со степенными разложениями (файл pseries): > p1:=powexp(sin(х));p1:= proc(powparm) … end proc > p2:=powexp(cos(x));p2 := proc(powparm) … end proc > tpsform(p1,x); 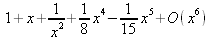 > tpsform(p2,x); 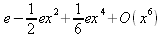 > a := powseries[powexp](x): > b := powseries[tpsform](a, x, 5); 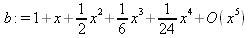 > с := powadd(powpoly(1+x^2+x,x), powlog(1+x)): > d := tpsform(c, x, 6); 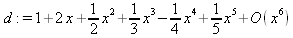 4.6.7. Maplet-иллюстрэция аппроксимации рядом Тейлора в рядДля демонстрации разложения аналитической функции в ряд имеется Maplet-инструмент Taylor Approximation. Для вызова его окна (рис. 4.19) нужно исполнить команду (в стандартном варианте интерфейса): Tools→Tutors→Calculus-Single Variables→Taylor Approximation…. 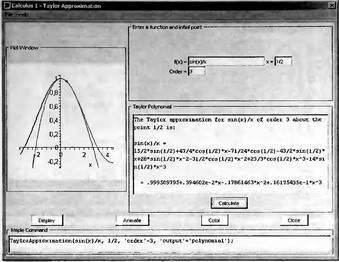 Рис. 4.19. Окно Maplet-демонстрации аппроксимации функции рядом Тейлора Нетрудно заметить, что это окно практически аналогично окну для демонстрации методов пошагового дифференцирования, описанному в разделе 4.3.4 (рис. 4.2). В связи с этим подробное описание средств и этого инструмента можно опустить. Отметим лишь, что он позволяет задавать функцию и значение x в точке разложения. По окончании работы с окном соответствующий предел и результат его вычисления появляется в окне документа. Можно просматривать постепенное улучшение приближения по мере увеличения порядка метода в режиме анимации. 4.7. Визуализация приложений математического анализаЛюбая СКМ имеет возможности для визуализации различных приложений математического анализа. Особое внимание этому уделено в системе Maple 9.5, где с помощью Maplet-средств созданы самоучители, обеспечивающие наглядное представление приложений математического анализа. 4.7.1. Суммы Римана и приближение интеграловЕсть два основных способа вычисления определенных интегралов в численном виде: • на основе сумм Римана (варианты метода прямоугольников); • на основе приближения подынтегральной функции той или иной зависимостью. Оба метода реализуются Maplet-инструментом Approximate Integration. Для вызова окна этого инструмента (рис. 4.20) нужно исполнить команду (в стандартном варианте интерфейса): Tools Tutors→Calculus-Single Variables→Approximate Integration…. Совершенно аналогичное окно выводит команда Tools→Tutors→Calculus-Single Variables→Rieman summs…. 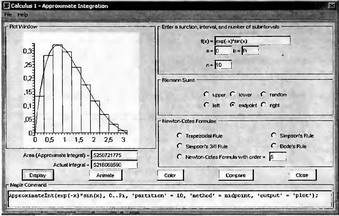 Рис. 4.20. Пример приближения интеграла суммой Римана (10 прямоугольников с центральным расположением) В правой части окна размещены панели: • ввода функции f(х), пределов а и b и числа интервалов разбиения • задания расположения прямоугольников, которые образуют сумму Римана; • методов Ньютона-Котеса; Относительно каждой ординаты прямоугольник может быть ориентирован сверху или снизу, справа или слева, посередине или даже случайным образом. При реализации формул приближения Ньютона-Котеса возможно применение метода трапеций, двух вариантов метода Симпсона (квадратичное приближение), метода Боде и известных формул Ньютона-Котеса заданного порядка (по умолчанию 5). В функциях численного интегрирования Maple тот или иной вид приближения можно задать явно, но по умолчанию метод выбирается автоматически. После выбора метода можно получить его графическую иллюстрацию (рис. 4.20), нажав мышью кнопку Display. Данный инструмент позволяет наблюдать в анимации повышение точности вычислений по мере увеличения числа прямоугольников — см. рис. 4.21. Для пуска анимации достаточно нажать мышью кнопку Animate. На рис. 4.21 показан промежуточный кадр анимации. В конце анимации закраска области интегрирования становится сплошной, после чего анимация циклически повторяется. 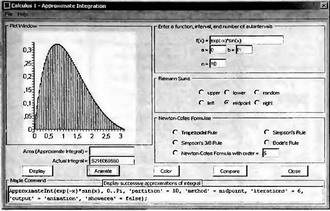 Рис. 4.21. Промежуточный кадр анимации, демонстрирующей приближение интеграла суммами Римана Приближение суммами Римана относится к довольно медленным методам интегрирования. Значительно повысить скорость интегрирования при заданной погрешности позволяют методы интегрирования повышенного порядка на основе формул Ньютона-Котесса. На рис. 4.22 показан пример приближения определенного интеграла на основе формулы Симпсона (параболического приближения подынтегральной функции). Из рисунка хорошо видно, что в этом случае (в отличие от рис. 4.20 при интегрировании методом прямоугольников) исходная подынтегральная функция и ее приближение отрезками парабол практически совпадают и на глаз их отличия выявить трудно. 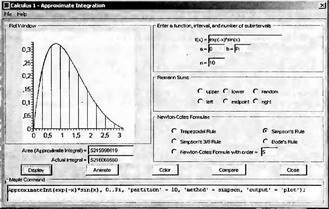 Рис. 4.22. Пример приближения интеграла методом Симпсона Кнопка Compare позволяет вывести таблицу с данными сравнения результатов интегрирования различными методами. Окно с этой таблицей представлено на рис. 4.23. Хорошо видно, что по мере повышения порядка метода интегрирования погрешность интегрирования уменьшается. 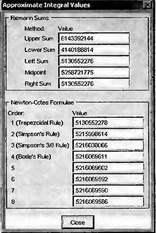 Рис. 4.23. Окно с результатами сравнения интегрирования различными методами 4.7.2. Вычисление длины дугиЕсли f(x) непрерывная на отрезке от а до b функция, то длина дуги этой функции (длина спрямленного отрезка) определяется известным выражением: 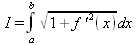 Для демонстрации вычисления длины дуги заданной аналитической функции имеется Maplet-инструмент ArcLench. Для вызова его окна (рис. 4.24) нужно исполнить команду (в стандартном варианте интерфейса): Tools→Tutors→Calculus-Single Variables→ArcLench…. 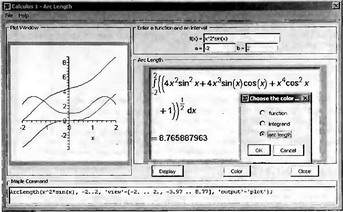 Рис. 4.24 Окно Maplet-инструмента для вычисления длины дуги Данный инструмент по заданной функции f(x) и значениям а и b вычисляет длину дуги, выводит ее значение и вид интеграла, а также строит график функции, ее производной и зависимости длины дуги, начинающейся в точке а от текущего значения х, меняющегося от а до b. Соответствующие графики, отличающиеся цветом кривых, показываются в левой части окна инструмента. Кнопка Color открывает окно выбора цвета из списка, который представлен окном Choose the color…, показанным внутри окна инструмента (см. рис. 4.24). Выбрав цвет нужной кривой нажатие кнопки OK можно вызвать панель выбора цветов Select a color, показанную на рис. 4.25. По завершении выбора цвета нужная кривая будет отображена в новом цвете.  Рис. 4.25 Панель выбора цвета 4.7.3. Иллюстрация теоремы о среднемПервая теорема о среднем гласит, что если f(x) интегрируемая функция, непрерывная на отрезке [a, b], то существует по крайней мере одно значение х=ξ в интервале [a, b], при котором 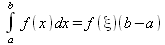 Иными площадь, определяемая интегралом может быть вычислена как площадь прямоугольника с основанием — отрезком ab и высотой f(ξ). Для иллюстрации этого положения служит Maplet-инструмент Mean Value Theorem. Его окно (рис. 4.26) открывается исполнением команды Tools→Tutors Calculus-Single Variables→Mean Value Theorem… Работа с окном вполне очевидна. На графике строится кривая функции, отрезок, проходящий через ее концевые точки, точка со значением х=с=ξ и касательная к ней. Главный результат — значение с=ξ . 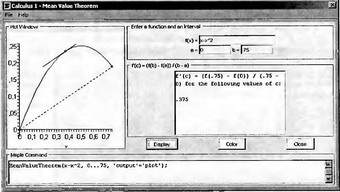 Рис. 4. 26. Окно Maplet-инструмента для иллюстрации первой теоремы о среднем 4.7.4. Построение касательной к заданной точке кривойДля построения касательной к заданной точке на кривой f(x) служит Марlet-инструмент Tangent. Его окно (рис. 4.27) открывается исполнением команды Tools→Tutors→Calculus-Single Variables→Tangent…. Работа с окном вполне очевидна. На графике строится кривая функции и касательная к заданной точке х. Наклон касательной определяется значением первой производной f'(x), значение которой Slope и уравнений касательной вычисляются.  Рис. 4.27. Окно Maplet-инструмента для иллюстрации построения касательной к заданной точке 4.7.5. Построение касательной к заданной точке кривой и секущих линийВ некоторых случаях, например при реализации метода Ньютона решения нелинейных уравнений, помимо построения касательной к заданной точке кривой f(x) нужно строить секущие линии и определять их точки пересечения с f(x). Для этого служит Maplet-инструмент Tangent and Secant. Его окно (рис. 4.28) открывается исполнением команды Tools→Tutors Calculus-Single Variables→Tangent and Secant…. Работа с окном вполне очевидна. На графике строится кривая функции и касательная к заданной точке х. Дополнительно строится ряд секущих. Возможно построение с применением анимации. 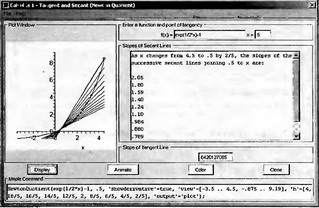 Рис. 4.28. Окно Maplet-инструмента для иллюстрации построения касательной к заданной точке и секущих линий 4.7.6. Вычисление поверхности вращения кривойПусть отрезок кривой f(х), при х в интервале [а,b] вращается вокруг оси 0х. Тогда площадь полученной фигуры вращения равна: 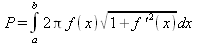 Для вычисления этой площади служит Maplet-инструмент Surface of Revolution. Его окно (рис. 4.29) открывается исполнением команды Tools Tutors→Calculus-Single Variables→Surface of Revolution…. Работа с окном вполне очевидна. На графике строится кривая функции и поверхность вращения этой кривой в 3D прямоугольной системе координат. Вычисляется значение площади. Вычисления возможны и при вращении отрезка кривой вокруг оси 0у. 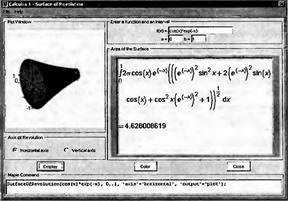 Рис. 4.29. Окно Maplet-инструмента для иллюстрации вычисления площади фигуры, полученной вращением отрезка кривой 4.7.7. Вычисление объема фигуры, полученной вращением отрезка кривойПусть отрезок кривой f(х), при х в интервале [a, b], вращается вокруг оси 0х. Тогда объем полученной фигуры вращения равен:  Для вычисления этого объема служит Maplet-инструмент Volume of Revolution. Его окно (рис. 4.30) открывается исполнением команды Tools→Tutors→Calculus-Single Variables→Volume of Revolution…. Работа с окном вполне очевидна. На графике строится кривая функции и поверхность вращения этой кривой в 3D прямоугольной системе координат. Вычисляется значение объема полученной фигуры. Вычисления возможны и при вращении отрезка кривой вокруг оси 0у. 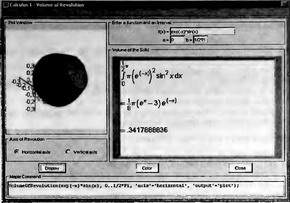 Рис. 4.30. Окно Maplet-инструмента для иллюстрации вычисления объема фигуры, полученной вращением отрезка кривой 4.8. Решение уравнений и неравенств4.8.1. Основная функция solveОдиночное нелинейное уравнение, например трансцендентное, можно задать в одной из двух форм: F(x) = 0 или f(x) = expr, expr — выражение. Второе уравнение всегда можно представить в виде F(x)=f(x)-expr=0, то есть в форме первого уравнения. При наличии аналитического решения оно находится путем поиска в ядре необходимых формул, описывающих такое решение. Но далеко не всегда нелинейные уравнения имеют аналитическое решение. В этом случае решение возможно численными методами. Maple 9.5 имеет мощные средства для решение линейных и нелинейных уравнений и неравенств. Так, для решения линейных и нелинейных уравнений в аналитическом виде используется достаточно универсальная и гибкая функция solve(eqn, var) или solve({eqn1,eqn2,...},{var1,var2,...}) где eqn — уравнение, содержащее функцию ряда переменных, var — переменная, по которой ищется решение. Если при записи eqn не используются знак равенства или знаки отношения, считается, что solve ищет корни уравнения eqn=0. Если eqn полином, то solve вычисляет все корни полинома — как действительные, так и комплексные. Характер решений можно изменить с помощью глобальных системных переменных: _EnvExplicit — при значении true выдает решение без применения конструкции RootOf; _EnvAllSolutions — при значении true задает выдачу всех решений; _SolutionsMayBeLost — при значении true дает решение, которое при обычном применении функции solve возвращает значения NULL; _MaxSols — задает максимальное число решений; _EnvTryHard — при значении true может дать компактное решение, но это может потребовать увеличения времени вычислений. В решениях могут встречаться следующие обозначения: _NN — указывает на неотрицательные решения; _В — указывает на решения в бинарной форме; _Z — указывает на то, что решение содержит целые числа; %N — при текстовом формате вывода задает общие члены решения и обеспечивает более компактную форму его представления. В форме solve[subtopic] возможны параметры subtopic функции solve следующих типов: floats functions identity ineq linear radical scalar series system При решении систем уравнений они и список переменных задаются как множества, то есть в фигурных скобках. При этом и результат решения получается в виде множества. Чтобы преобразовать его к обычному решению, нужно использовать функцию assign, которая обеспечивает присваивание переменным значений, взятых из множества. Функция solve старается дать решение в аналитическом виде. Это не означает, что ее нельзя использовать для получения корней уравнений в численном виде. Просто для этого придется использовать функции evalf или convert. Если результат решения представлен через функцию RootOf, то зачастую можно получить все корни с помощью функции allvalues. 4.8.2. Решение одиночных нелинейных уравненийРешение одиночных нелинейных уравнений вида f(х)=0 легко обеспечивается функций solve(f(x),x). Это демонстрируют следующие примеры (файл solve): > solve(х^3-2*х+1,х); 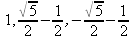 > solve(х^(3/2)=3,х);3(2/3) > evalf(%);2.080083823 > solve(sqrt(ln(х))=2,х);e4 > evalf(%);54.59815003 Если уравнение записывается без правой части, то это означает, что она равна нулю. Часто бывает удобно представлять уравнение и его решение в виде отдельных объектов, отождествленных с определенной переменной (файл solve): > eq:=(2*х^2+х+3=0);eq := 2x²+x+3 = 0 > s: = [solve(eq,x)]; 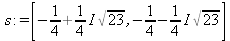 В частности, это позволяет легко проверить решение (даже если оно не одно, как в приведенном примере) подстановкой (subs): > subs(x=s[1],eq); 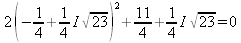 > subs(x=s[2],eq); 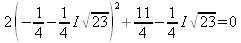 > evalf(%);0. + 0.I = 0. Сводящиеся к одному уравнению равенства вида f1(х)=f2(x) также решаются функцией solve(f1(x)=f2(x),x): > solve(х^4=-х-1,х);RootOf(_ Z4 + _Z + 1, index = 1), RootOf (_Z4 + _Z + 1, index = 2), RootOf(_Z4 + _Z + 1, index = 3), RootOf(_ Z4 +_Z + 1, index = 4) > evalf(%);.7271360845 + .9340992895 I, -.72711360845 + .4300142883 I, -.7271360845 - .4300142883 I, .7271360845 - .9340992895 I > solve({exp(x)=sin(x)},x);{x = RootOf(_ Z-ln(sin(_Z)))} > evalf(%);{x = .3627020561 - 1.133745919I} > solve(x^4=2*x,x); 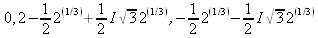 > evalf(%);0., 1.259921050, -.6299605250 + 1.091123636 I, -.6299605250 - 1.091123636 I Обратите внимание в этих примерах на эффективность применения функции evalf, позволяющей получить решения, выраженные через функцию RootOf, в явном виде. Некоторые даже с виду простые уравнения могут дать неожиданные для многих пользователей результаты. Пример такого рода приведен ниже (файл solve): > restart;eq:=ехр(-х)=х;sol:=solve(exp(-х)=х,х);eq := е(-х) = х sol = LambertW(1) > evalf(sol);0.5671432904 В данном случае решение получено через значение специальной функции Ламберта. Впрочем, с помощью функции evalf его можно представить в численном виде. 4.8.3. Решение тригонометрических уравненийФункция solve может использоваться для решения тригонометрических уравнений: > solve (sin (х) =.2, х);.2013579208 > solve(sin(х)-1/2,х); 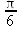 > solve(cos(х)=.5, х);1.047197551 Однако из приведенных примеров видно, что при этом найдено только одно (главное) решение. Оно ищется в интервале [-π, π]. Периодичность тригонометрических функций и связанная с этим множественность решений оказались проигнорированы. Однако можно попытаться найти все периодические решения, выполнив следующую команду: > _EnvAllSolutions:=true;_EnvAllSoIutions := true Указанная в ней системная переменная отвечает за поиск всех периодических решений, когда ее значение равно true, и дает поиск только главных решений при значении false, принятом по умолчанию. Так что теперь можно получить следующее: > solve(sin(х)=1/2,х); 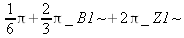 Здесь вспомогательные переменные _ВI~ и _ZI~ могут иметь только целочисленные значения (знак ~ означает, что на них наложено ограничение — в нашем случае в виде целочисленности возможных значений). На рис. 4.31 показан более сложный случай решения нелинейного уравнения вида f1(х)=f2(x), где f1(х)=sin(x) и f2(х)=cos(x)-1. Решение дано в графическом виде и в аналитическом для двух случаев — нахождения главных значений корней и нахождения всех корней. Обратите внимание на команду _EnvAllSolutions:=true задающую поиск всех корней. 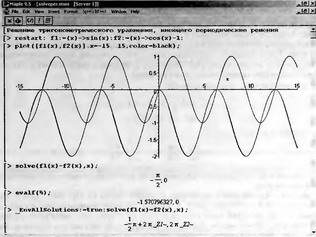 Рис. 4.31. Пример решения уравнения, имеющего периодические решения В подобных решениях встречаются переменные _В1~ и означающие ряд натуральных чисел. Благодаря этому через них можно представить периодически повторяющиеся решения. Примеры решения уравнений с обратными тригонометрическими функциями показаны ниже: > eqns := 2*arcsin(x) — arccos(5*x);eqns := 2 arcsin(x) - arccos(5x) > solve(eqns, {x}); 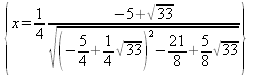 > eqns := arccos(x) — arctan(x/2);eqns := arccos(x) - arctan(½x) > solve(eqns, {x}); 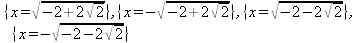 4.8.4. Решение систем линейных уравненийДля решения систем линейных уравнений созданы мощные матричные методы, которые будут описаны отдельно в Главе 6. Однако функция solve также может успешно решать системы линейных уравнений, причем в символьном (аналитическом) виде. Такое решение в силу простоты записи функции может быть предпочтительным. Для решения система уравнений и перечень неизвестных задаются в виде множеств (см. приведенный ниже пример): > eq1:=а*х+b*у=е; eq2:=c*x+d*y=f;eq1 := ах + by = е eq2 := cx + dу = f > solve({eq1,eq2},{x,y});  В данном случае решение системы из двух линейных уравнений представлено в символьном виде. Рисунок 4.32 дает еще два примера решения систем из двух линейных уравнений на этот раз в численном виде. В первом примере функция solve возвращает решение в виде значений неизвестных x и у, а во втором отказывается это делать. 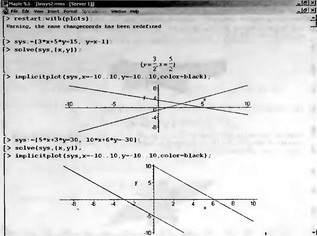 Рис. 4.32. Примеры решения системы из двух линейных уравнений с графической иллюстрацией В чем дело? Оказывается, в том, что во втором случае система просто не имеет решения. Импликативная графика пакета расширения plots дает прекрасную возможность проиллюстрировать решение. Так, нетрудно заметить, что в первом случае геометрическая трактовка решения сводится к нахождению точки пересечения двух прямых, отображающих два уравнения. При этом имеется единственное решение, дающее значения x и у для этой точки. Во втором случае решения и впрямь нет, ибо уравнения задают параллельно расположенные прямые, которые никогда не пересекаются. Рекомендуем читателю самостоятельно проверить и третий случай — бесконечного множества решений. Он имеет место, если оба уравнения описывают одну и ту же зависимость и их графики сливаются в одну прямую. Решение систем из трех линейных уравнений также имеет наглядную геометрическую интерпретацию — в виде точки, в которой пересекаются три плоскости, каждая из которых описывается функцией двух переменных. Для наглядности желательно представить и линии пересечения плоскостей. Это позволяет сделать функция импликативной трехмерной графики implicitplot3d, что и показано на рис. 4.33. Для объединения графиков площадей использована функция display.  Рис. 4.33. Пример решения системы из трех линейных уравнений с графической иллюстрацией решения Некоторые проблемы с решением систем из трех линейных уравнений иллюстрируют примеры, приведенные на рис. 4.34. В первом примере решения вообще нет. График показывает, в чем дело — линии пересечения плоскостей идут параллельно и нигде не пересекаются. Во втором примере все три плоскости пересекаются по одной линии.  Рис. 4.34. Графическая иллюстрация особых случаев решения системы из трех линейных Следующий пример показывает решение системы из четырех линейных уравнений: > sys := { 4*x1 + 7*х2 - х3 + 3*х4 = 11, -2*х1 + 2*х2 - 6*х3 4+ х4 = 4, x1 - 3*х2 + 4*x3 - х4 = -3, 3*х1 - 5*х2 - 7*х3 + 5*х4 = 8 }: > solve(sys, {x1, х2, х3, х4}); 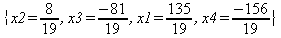 Эта система имеет решение, но его простая графическая иллюстрация уже невозможна. Случай решения неполной системы уравнений (уравнений — 3, а неизвестных — 4) иллюстрирует следующий пример: > sys := { x1 + 2*х2 + 3*х3 + 4*х4 = 51, x1 - 3*х2 + 4*х3 + х4 = 32, х1 + 2*х2 - 6*х3 + х4 = -23 }: > solve(sys, {x1, х2, х3, х4 }); 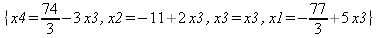 Как видно из приведенных примеров, функция solve неплохо справляется с решением систем линейных уравнений. 4.8.5. Решение систем нелинейных и трансцендентных уравненийФункция solve может использоваться для решения систем нелинейных и трансцендентных уравнений. Для этого система уравнений и перечень неизвестных задаются в виде множеств. Ниже приведены примеры решения уравнений (файл solvenl): > restart; > solve{{х*у=а,x+y=b},{х,у});у = RootOf(_Z² - _Zb + а), х = -RootOf(_Z² -_Zb + a)+b) > allvalues(%); 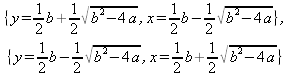 > s:=solve({x*y=2,x+y=3},{x,y});s:={y = 1, x = 2}, {y = 2, x = 1} > assign(s); x; y;1 2 > unassign('x'); y:= 'y';y:= y > [x, y];[x,y] В этих примерах хорошо видна техника работы с функциями solve и assign. В конце примеров показано восстановление неопределенного статуса переменных х и у с помощью функции unassign и снятие определения переменных с помощью заключения их в прямые апострофы. Приведем еще один пример решения системы нелинейных уравнений с проверкой правильности решения с помощью функции eval: > eqs: = {2*х+4*у=6,у+1/х=1}; 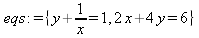 > r:=solve(eqs, {х, у});r:= {y = 2, х = -1}, {у = ½, х = 2} > eval(eqs,r[1]);{1 = 1, 6 = 6} > eval(eqs,r[2]);{1 = 1, 6 = 6} Для проверки всех решений можно использовать также функции map и subs: > map(subs,[r],eqs);[{1 = 1, 6 = 6}, {1 = 1, 6 = 6}] Maple имеет и еще ряд возможностей для проверки решений, но представленных обычно вполне достаточно для такой проверки. Ее следует принять за правило при выполнении решений уравнений. 4.8.6. Функция RootOfВ решениях уравнений нередко появляется функция RootOf, означающая, что корни нельзя выразить в радикалах. Эта функция применяется и самостоятельно в виде RootOf(expr) или RootOf(expr, х), где expr — алгебраическое выражение или равенство, х — имя переменной, относительно которой ищется решение. Если переменная х не указана, ищется универсальное решение по переменной _Z. Когда expr задано не в виде равенства, решается уравнение expr=0. Для получения решений вида RootOf в явном виде может использоваться функция allvalues. Примеры применения функции RootOf (файл RootOf): > RootOf(х^2+1=0,х);RootOf (_Z² + 1) > allvalues(%);I, -I > RootOf(а*b^2+а/b,b);RootOf(_Z³ + 1) > allvalues(%);-1, ½ +½I√3, ½-½I√3 > RootOf(x^3-1,x) mod 7;RootOf(_Z³ + 6) > allvalues(%);-6(1/3), ½6(1/3) - ½I√3 6(1/3), ½6(1/3) + ½I√3 6(1/3) > evalf(%);-1.817120593, .9085602965-1.573672596 I, .908560296+1.573672596 I > RootOf(х^2-2*х+1,х) mod 5;1 Итак, функция RootOf является эффективным способом представления решения в компактном виде. Как уже отмечалось, наряду с самостоятельным применением она часто встречается в составе результатов решения нелинейных уравнений. 4.8.7. Решение уравнений со специальными функциямиК важным достоинствам Maple относится возможность решения уравнений, содержащих специальные функции как в записи исходных выражений, так и в результатах решения. Приведем несколько примеров такого рода (файл solvesf): > restart:eqn := Psi(3*x-99) - Psi(3*x-100) + 3/х^2=0; 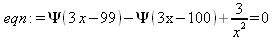 > r:=solve(eqn, {х}); 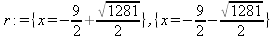 > eqn := max(x,3*x-12)=min(10*x+8, 22-x);eqn := max(x, - 12 + 3x) = min(10x + 8, 22 - x) > r:=solve(eqn, {x}); 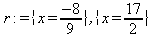 > map(subs,[r],eqn); 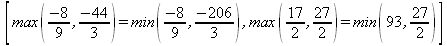 > eqn := LambertW(3*x)=ln(x);eqn := LambertW(3x) = ln(x) > r:=solve(eqn, {x});r:= {x = e³} > map(subs, [r], eqn);[LambertW(3e³) = ln(e³)] > evalf(map(subs,[r], eqn));[3.000000000 = 3.000000000] Полезно обратить внимание на не вполне обычную проверку правильности решений. Иногда при этом выводятся значения левой и правой частей уравнения, требующие осмысления полученных результатов. 4.8.8. Решение неравенствНеравенства в математике встречаются почти столь же часто, как и равенства. Они вводятся знаками отношений, например > (больше), < (меньше) и т.д. Решение неравенств существенно расширяет возможности функции solve. При этом неравенства задаются так же, как и равенства. Приведенные на рис. 4.35 примеры поясняют технику решения неравенств. 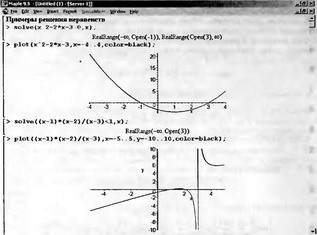 Рис. 4.35. Примеры, иллюстрирующие решение неравенств Из приведенных примеров очевидна форма решений — представлены критические значения аргумента, вплоть до не включаемых значений области действия неравенства (они указываются словом Open). Всегда разумным является построение графика выражения, которое задает неравенство — это позволяет наглядно убедиться в правильности решения. Приведем еще несколько примеров решения неравенств в аналитической форме (файл solveu): > solve(5*х>10,х);RealRange(Open(2), ∞) > solve(5*х>=10,х);RealRange(2, ∞) > solve(ln(х)>2,х);Rea1Range(Open(e²), ∞) > solve(ехр(х)>10, х);RealRange(Open(ln(10)), ∞ > solve(a*x>b,{х}); 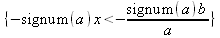 > eqn := abs(z)^2/(z+1) < ехр(2)/(ехр(1)-1); 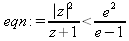 > solve(eqn, {z}); 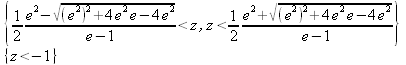 > eqn := ехр(х)*х^2 >= 1/2; 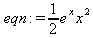 > solve(eqn, {x}); 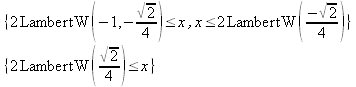 > eqns := abs((z+abs(z+2))^2-1)^2 = 9;eqns := |(z +|z + 2|)² - 1|² = 9 > solve(eqns, {z});{z = 0 }, { z ≤ -2} > eqns := { х^2<1, у^2<=1, х+у<1/2 };eqns:={х² < 1, y² ≤ 1, х + y < ½} > solve(eqns, {x, у});{y ≤ 1, -1 ≤ y, x+y < ½, -1 < x, x < 1} В последнем примере показано решение системы неравенств. При этом выдаются области определения нескольких переменных. 4.8.9. Решение функциональных уравненийРешение функционального уравнения, содержащего в составе равенства некоторую функцию f(х), заключается в нахождении этой функции. Для этого можно использовать функцию solve, что демонстрируют приведенные ниже примеры (файл solvefe): > A:=solve(f(х)^2-х+1,f);А := proc(x) RootOf(_Z^ 2 -х + 1, label =_L7) end proc > convert(A(x),radical); 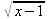 > allvalues(%); 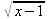 > B:=solve(f(x)*x=ln(x^2),f);В := proc(x) ln(x^2)/x end proc > convert(B(x),radical); 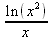 > C:=solve(f(x)*х^2=а*х^2+b*х+с, f);C := proc(x) (ax×x^2 + bx×x + c)/x^2 end proc > convert(C(x),radical); 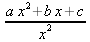 4.8.10. Решение уравнений с линейными операторамиMaple позволяет решать уравнения с линейными операторами, например, с операторами суммирования рядов и дифференцирования. Ограничимся одним примером такого рода (файл solvefo): > S := sum((a+b*exp(x[i])-y[i])^2, i=0..n); 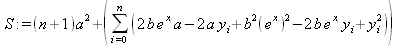 > eqns := {diff(S, a), diff(S,b)}; 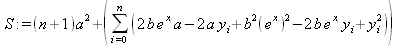 > solve(eqns, {a, b}); 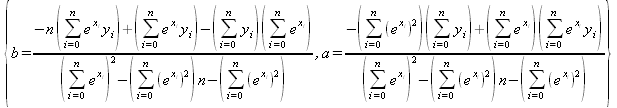 4.8.11. Решение в численном виде — функция fsolveДля получения численного решения нелинейного уравнения или системы нелинейных уравнений в формате вещественных чисел удобно использовать функцию fsolve(eqns, vars, options) Эта функция может быть использована со следующими параметрами: complex — находит один или все корни полинома в комплексной форме; fulldigits — задает вычисления для полного числа цифр, заданного функцией Digits; maxsols=n — задает нахождение только n корней; interval — задается в виде а..b или х=а..b или {x=a..b, y=c..d, …} и обеспечивает поиск корней в указанном интервале. Функция fsolve дает решения сразу в форме вещественных или комплексных чисел, что и показывают следующие примеры (файл fsolve): > fsolve(sin(х)=Pi/4,х);.9033391108 > fsolve(sin(х)=1/2,х=4..8);6.806784083 > fsolve(2*х^2+х-1=10,x);-2.608495283, 2.108495283 > fsolve(х^5-х,x);-1., 0., 1.000000000 > fsolve(х^5-х,x,complex);-1.000000000, -1.000000000 I, 0., 1.000000000 I, 1.000000000 > eqns := abs(x)*x+exp(x) > 0;eqns:= 0 <|x|x +ex > solve(eqns, {x});{-2 LambertW(½)<x} > f := sin(x+y) — exp(x)*y = 0: g := x^2 - у = 2: fsolve{{f,g},{x,y},{x=-1..1,y=-2..0});{x = -.6687012050, у = -1.552838968} Заметим, что локализация поиска корней в заданном интервале позволяет отыскивать такие решения, которые не удается получить с помощью функций solve и fsolve в обычном применении. В последнем из приведенных примеров дается решение системы нелинейных уравнений, представленных уравнениями f и g. Чтобы еще раз показать различие между функциями solve и fsolve, рассмотрим пример решения с их помощью одного и того же уравнения erf(x) = 1/2: > solve(erf(х)=1/2,х);RootOf(2 erf(_Z) -1) > fsolve(erf(x)=1/2);.4769362762 Функция solve в этом случае находит нетривиальное решение в комплексной форме через функцию RootOf, тогда как функция fsolve наводит обычное приближенное решение. Мы уже отмечали, что функция solve дает решение уравнения ехр(-х) = х в форме специальной функции Ламберта. Нетрудно заметить, что функция fsolve дает результат сразу в форме числа с плавающей точкой: > restart;eq:=exp(-х)=х;sol:=fsolve(ехр(-х)=х,х);eq: = e(-x) = х sol: =0.5671432904 4.8.12. Решение рекуррентных уравнений — rsolveФункция solve имеет ряд родственных функций. Одну из таких функций — fsolve — мы рассмотрели выше. В справочной системе Maple можно найти ряд и других функций, например rsolve для решения рекуррентных уравнений, isolve для решения целочисленных уравнений, msolve для решения по модулю m и т.д. Здесь мы рассмотрим решение уравнений важного класса — рекуррентных. Напомним, что это такие уравнения, у которых заданный шаг решения находится по одному или нескольким предшествующим шагам. Для решения рекуррентных уравнений используется функция rsolve: rsolve(eqns, fens) rsolve{eqns, fens, 'genfunc'(z)) rsolve(eqns, fens, 'makeproc') Здесь eqns — одиночное уравнение или система уравнений, fens — функция, имя функции или множество имен функций, z — имя, генерирующее функциональную переменную. Ниже представлены примеры применения функции rsolve (файл rsolve): > restart; > rsolve(f(n)=-2*f(n-1)-f(n-2), f(k));(-f(0) -f(1))(k + 1)(-1)k +(f(1) +2f(0))(-1)k > rsolve({f(n)=-3*f(n-1)-2*f(n-2),f(1..2)=1), {f});{f(w) = -3(-1)n +(-2)n} > rsolve({y(n)=n*y(n-1), y(0)=1),y);Г(n + 1) > rsolve((y(n)*y(n-1)+y(n)-y(n-1)=0,у(0)=a},y); 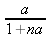 > rsolve({F(n)=F(n-1)+F(n-2),F(1..2)=1),F, 'genfunc'(x)); 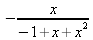 > rsolve({y(n+1)+f(n)=2*2^n+n, f(n+1)-y(n)=n-2^n+3, y(k=1..5)=2^k-1,f(5)=6), {y, f});{f(n)=n+1, y(n) = 2n - 1} А теперь приведем результат вычисления функцией rsolve n-го числа Фибоначчи. Оно задается следующим выражением: > eq1 := (f(n+2) = f(n+1) + f(n), f(0) = 1, f(1) = 1};eq1 := {f(n+2) = f(n+1)+f(n), f(0) = 1, f(1) = 1} В нем задана рекуррентная формула для числа Фибоначчи — каждое новое число равно сумме двух предыдущих чисел, причем нулевое и первое числа равны 1. С помощью функции rsolve в Maple 9.5 можно получить поистине ошеломляющий результат: > a1:=rsolve(eq1, f); 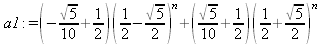 Числа Фибоначчи — целые числа. Поэтому представленный результат выглядит как весьма сомнительный. Но на самом деле он точный и с его помощью можно получить числа Фибоначчи (убедитесь в этом сами). Любопытно отметить, что решение в Maple8 заметно отличается от приведенного выше для Maple 9.5. Но только по форме, а не по сути. 4.8.13. Решение уравнений в целочисленном виде — isolveИногда бывает нужен результат в форме только целых чисел. Для этого используется функция isolve(eqns, vars), дающая решение в виде целых чисел. Приведем примеры ее применения (файл isolve): > isolve({2*х-5=3*y});{x=4 + 3_Z1, у = 1+2_Z1} > isolve(y^4-z^2*y^2-3*х*z*y^2-х^3*z); 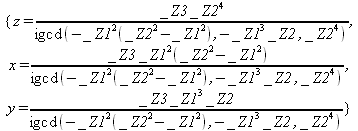 Здесь вывод представлен с помощью вспомогательных переменных _Z1. 4.8.14. Функция msolveФункция msolve(eqns,vars,m) или msolve(eqns,m) обеспечивает решение вида Z mod m (то есть при подстановке решения левая часть при делении на m дает остаток, равный правой части уравнения). При отсутствии решения возвращается объект NULL (пустой список). Ниже даны примеры использования функции msolve (файл msolve): > msolve{{3*х-4*y=1,7*х+y=2},12);{y = 5, х = 3} > msolve(2^i=3,19);{i = 13 + 18 _ZI~} > msolve(8^j=2,х,17);{j = 3 + 8х} На этом мы завершаем рассмотрение функций системы Maple 9.5 для решения уравнений, неравенств и систем с ними. 4.9. Применение пакета расширения student4.9.1. Функции пакета studentПакет student — это, несомненно, один из пакетов, наиболее привлекательных для студентов и аспирантов. В нем собраны наиболее распространенные и нужные функции, которые студенты университетов и иных вузов обычно используют на практических занятиях, при подготовке курсовых и дипломных проектов. Пакет вызывается командой: > with(student); Ниже представлено назначение функций этого пакета, включая некоторые функции из его более ранних версий: D — дифференциальный оператор; Diff — инертная форма функции вычисления производной; Doubleint — инертная форма функции вычисления двойного интеграла; Int — инертная форма функции интегрирования int; Limit — инертная форма функции вычисления предела limit; Lineint — инертная форма функции вычисления линейного интеграла lineint; Point — тестирование объекта на соответствие типу точки (point); Product — инертная форма функции вычисления произведения членов последовательности; Sum — инертная форма функции вычисления суммы членов последовательности; Tripleint — инертная форма функции вычисления тройного интеграла; changevar — замена переменной; combine — объединение подобных членов; completesquare — вычисление полного квадрата (многочлена); distance — вычисление расстояния между точками; equate — создание системы уравнений из списков, таблицы, массивов; extrema — вычисление экстремума выражения; integrand — вывод подынтегрального выражения из под знака инертного интеграла; intercept — нахождение точки пересечения двух кривых; intparts — интегрирование по частям; isolate — выделение подвыражения; leftbox — графическая иллюстрация интегрирования методом левых прямоугольников; leftsum — числовое приближение к интегралу левыми прямоугольниками; makeproc — преобразование выражения в процедуру Maple; maximize — вычисление максимума функции; middlebox — графическая иллюстрация интегрирования метолом центральных прямоугольников; middlesum — числовое приближение к интегралу центральными прямоугольниками; midpoint — вычисление средней точки сегмента линии; minimize — вычисление минимума функции; powsubs — подстановка для множителей выражения; rightbox — графическая иллюстрация интегрирования методом правых прямоугольников; rightsum — числовое приближение к интегралу правыми прямоугольниками; showtangent — график функции и касательной линии; simpson — числовое приближение к интегралу по методу Симпсона; slope — вычисление и построение касательной к заданной точке функции; trapezoid — числовое приближение к интегралу методом трапеций; value — вычисляет инертные функции. В Maple 8/9 число функций этого пакета было несколько сокращено в сравнении с Maple 7, так что надо быть внимательным при его использовании в практических вычислениях — некоторые документы с функциями этого пакета, подготовленные в среде Maple 7, могут не работать в среде Maple 8/9/9.5. 4.9.2. Функции интегрирования пакета studentВ ядре и в пакетах расширения Maple 8/9/9.5 можно найти множество специальных функций для вычисления интегралов различного типа. Например, в пакете student имеются следующие функции: Int(expr,x) — инертная форма вычисления неопределенного интеграла; Doubleint(expr,x,у,Domain) — вычисление двойного интеграла по переменным х и у по области Domain; Tripleint(expr,x,y,z) — вычисление тройного интеграла; intparts(f,u) — интегрирование по частям. Ниже дан пример применения функции Tripleint пакета student: > Tripleint(f(х,у,z),х,у,z);∫∫∫(x,y,z)dxdydz > Tripleint(х*у*z^2,x=0..2,y=0..3,z=0..5); 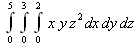 > evalf(%);375.0000000 > int(int(int(x*y*z^2,x=0..2),y=0..3),z=0..5);375 4.9.3. Иллюстративная графика пакета studentПакет student имеет три графические функции для иллюстрации интегрирования методом прямоугольников: leftbox(f(x), x=a..b, о) или leftbox(f(x), x=a..b, n, 'shading'=<color>, о); rightbox(f(x), x=a..b, о) или rightbox(f(x), x=a..b, n, o); middlebox(f(x), x=a..b, о) или middlebox(f(x), x=a..b, n, o); Здесь f(x) — функция переменной x, x — переменная интегрирования, a — левая граница области интегрирования, b — правая граница области интегрирования, n — число показанных прямоугольников, color — цвет прямоугольников, о — параметры (см. ?plot,options). В этих функциях прямоугольники строятся соответственно слева, справа и посередине относительно узловых точек функции f(х), график которой также строится. Кроме того, имеется функция для построения касательной к заданной точке х=а для линии, представляющей f(x): showtangent(f(х), х=а) Рисунок 4.36 показывает все эти возможности пакета student. Четыре отмеченных вида графиков здесь построены в отдельных окнах. 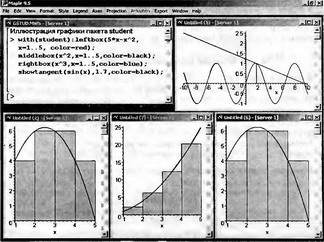 Рис. 4.36. Примеры иллюстративной графики пакета student Графические средства пакета student ограничены. Но они предоставляют как раз те возможности, которые отсутствуют в основных средствах построения графиков. В Maple 9/9.5 функции пакета резко расширены и мы вернемся к их рассмотрению в Главе 9. 4.9.4. Визуализация методов численного интегрированияПакет Student обеспечивает визуализацию ряда методов численного интегрирования: методов прямоугольников с различным расположением их, метода трапеций и метода парабол (Симпсона). Это возможно в символьном виде, например (файл intvis): > with(student): middlesum(x*exp(-x), x=a..b); 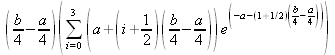 Ниже представлено несколько примеров такой визуализации (для метода прямоугольников со средним расположением их, метода трапеций и метода Симпсона): > with(student): middlesum(х*exp(-x), x=0..4); 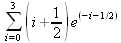 > trapezoid(х*ехр(-х), x=0..4); 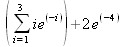 > simpson(x*sin(-х), х=1..4); 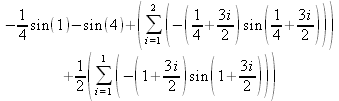 > evalf(%)-1.5719966508305 В последнем примере показано вычисление по представлению методом Симпсона. 4.10. Работа с алгебраическими кривыми4.10.1. Пакет для работа с алгебраическими кривыми algcurvesДля работы с алгебраическими кривыми служит пакет расширения algcurves. Он загружается командами: > restart;with(algcurves); Ввиду важности функций пакета приведем полную форму записи и назначение наиболее важных функций этого пакета: Weierstrassform(f,x,y,x0,y0,opt) — вычисление нормальной формы для эллиптических или гиперболических алгебраических кривых; differentials(f, x, у, opt) — голоморфные дифференциалы алгебраических кривых; genus(f,x,y,opt) — подлинность алгебраической кривой; homogeneous(f,x,y,z) — создание полинома двух переменных, гомогенного в трех переменных; homology(f, х, у) — находит канонический гомологический базис по алгоритму Треткоффа; integral_basis(f, х, у, S) — интегральный базис алгебраического поля функции; is_hyperelliptic(f, х, у) — тестирует кривую на ее принадлежность к гиперболической; j_nvariant(f,x,y) — j-инвариант алгебраической кривой; monodromy(f, х, у, opt) — вычисляет монодромию алгебраической кривой; parametrization(f,x,y,t) — находит параметризацию для кривой с родом (даваемым функцией genuc), равным 0; periodmatrix(f, х, у, opt) — вычисляет периодическую матрицу кривой; plot_knot(f,x,y,opt) — строит узел — несамопересекающуюся замкнутую кривую в трехмерном евклидовом пространстве; puiseux(f,x=p,y,n,T) — определяет Пуизе-расширение алгебраической функции (может иметь и более простые формы записи); singularities(f,x,y) — анализирует кривую на сингулярность. 4.10.2. Примеры работы с алгебраическими кривымиПриведем также примеры применения функций пакета Algcurves (файл algcurve): > Weierstrassform((y^2-1)^2+x*(x^2+1)^2, x,y,x0,y0); 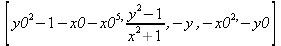 > f:=у^3+х^3*у^3+х^4;f := y3 + y3x3 + x4 > differentials(f, х, у); 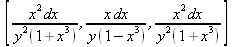 > differentials(f,x,у,skip_dx);[x², yx, yx²] > nops(%);3 > genus(f, x, y);3 > homogeneous(f, x, y, z);x4z2 +y3x3 +у3x3 > g := y^3-х*y^2+2*2^(1/2)*y^2+х^2-2*2^(1/2)*х+2+y^6;g := y3 - xy2 + 2√2 у2 + x2- 2√2x + 2 + y6 > integral_basis(g,x,y); 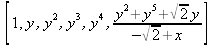 > is_hyperelliptic(f, x, y);false > f1:=у^2+х^5+1:is_hyperelliptic(f1, x, y);true > j_invariant(g,x,y); 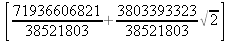 > parametrization(х^4+y^4+а*х^2*y^2+b*y^3,х,y,t); 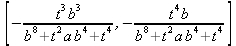 > Z := periodmatrix(f1,х,у,Riemann); 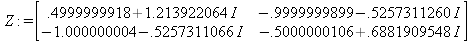 4.10.3. Построение алгебраических кривых класса knotФункция plot_knot позволяет строить одну или несколько алгебраических кривых — узлов. Пример построения целого семейства узлов показан на рис. 4.37.  Рис. 4.37. Семейство узлов Для лучшего обзора таких кривых рекомендуется воспользоваться возможностью вращения трехмерных фигур мышью для уточнения угла, под которым рассматривается фигура — в нашем случае семейство алгебраических кривых. Начиная с версии Maple 7 в пакет расширения Algcurves добавлена новая функция импликативной графики plot_real_curve. Она строит алгебраическую кривую для действительной части полиномиального выражения и записывается в виде: plot_real_curve(р, х, у, opt) Функция имеет следующие параметры: p — полиномиальное выражение переменных x и у задающее алгебраическую кривую; opt — параметр, который может быть записан в форме приведенных ниже выражений: showArrows=true или false — задает показ стрелок касательных или перпендикулярных к точкам вдоль кривой (по умолчанию false); arrowIntervalStep=posint — задает число точек, пропускаемых до показа очередной пары стрелок (по умолчанию 10); arrowScaleFactor=positive — задает масштаб для длины стрелок (по умолчанию 1); colorOfTangentVector=с — задает цвет касательных стрелок, по умолчанию заданный как зелёный, COLOR(RGB,0,1.0); colorOfNormalVector=с — задает цвет перпендикулярных стрелок, по умолчанию заданный как красный, COLOR(RGB,1,0,0); colorOfCurve=с — задает цвет кривой, по умолчанию заданный как синий, COLOR(RGB, 0, 0, 1); eventTolerance=positive — задает погрешность при представлении сингулярных точек (по умолчанию 0,01). NewtonTolerance=positive — задает погрешность при выполнении ньютоновских итераций в ходе построений. Функция plot_real_curve вычисляет и строит алгебраическую кривую по точкам. Применение функции plot_real_curve показывает рис. 4.38.  Рис. 4.38. Примеры применения функции plot_real_curve 4.11. Векторные вычисления и функции теории поля4.11.1. Пакет векторных вычислений VectorCalculusВ Maple 8 были существенно расширены возможности вычислений над векторами (пространственными объектами) и поверхностями. Для этого введен пакет VectorCalculus, который, при вызове, открывает доступ ко многим командам и функция векторного анализа, теории поля и приложений дифференциального исчисления [67, 68] (файл vc): > restart; with(VectorCalculus); interface(showassumed=0); Warning, the assigned names <,> and <|> now have a global binding Warning, these protected names have been redefined and unprotected: *, +, Vector, diff, int, limit, series[&x, *, +, ., <, >, <|>, AddCoordinates, ArcLength, BasisFormat, Binormal, CrossProduct, Curl, Curvature, Del, DirectionalDiff, Divergence, DotProduct, Flux, GetCoordinateParameters, GetCoordinates, Gradient, Hessian, Jacobian, Laplacian, LineInt, MapToBasis, Nabla, PathInt, PrincipalNormal, RadiusOfCurvature, ScalarPotential, SetCoordinateParameters, SetCoordinates, SurfaceInt, TNBFrame, Tangent, TangentLine, TangentPlane, TangentVector, Torsion, Vector, VectorField, VectorPotential, Wronskian, diff, evalVF, int, limit, series] Нетрудно заметить, что данный пакет после загрузки видоизменяет многие операторы, команды и функции, встроенные в ядро системы. При этом меняется их математический и физический смысл. Поэтому пользоваться пакетом надо с известной осторожностью. Для восстановления роли функций можно использовать команду restart. Пакет VectorCalculus ориентирован в первую очередь на решение задач математической физики, использующих методы теории поля и приложения дифференциального исчисления. Он оперирует такими привычными для физиков (разумеется, и для математиков) понятиями, как поток векторного поля, градиент, тор-сион, векторный потенциал и др. Приведенный ниже материал поясняет применение большинства функций этого пакета. Полезно просмотреть и файл VectorCalculus.mws, содержащий примеры его применения. В Интернете можно найти целую серию уроков по векторному анализу и теории поля в виде пакета Calculus IV или V (разработчик проф. J. Wagner). 4.11.2. Объекты векторных вычисленийВектор в геометрическом представлении в данном пакете по умолчанию задается в прямоугольной системе координат: > v := Vector( [x,y,z]);v := хех + yey + zez Здесь ех, еу и еz — проекции единичного вектора е на оси координат х, у и z. Тип координатной системы (по умолчанию — прямоугольная) можно определить следующим образом: > attributes(v);coords = cartesian Для создания векторного поля служит функция VectorField(v, с) где v — вектор и с — опционально заданный параметр в форме name[name, name,...], задающий тип координатной системы. Можно изменить систему координат, например, задав (с помощью функции установки координат SetCoordinates) полярную систему координат: > SetCoordinates(polar);polar > w := <r,theta>;w: = r er + θ e0 > attributes(w);coords = polar Аналогично можно задать вектор в сферической системе координат: > SetCoordinates(spherical[r,phi,theta]);sphericalr,φ,θ > F := VectorField(<r,0,0>);F.= rēr > attributes(F);vectorfield, coords = sphericalr,φ,θ Можно также сменить формат представления вектора и выполнить с ним некоторые простейшие векторные операции: > BasisForrnat(false);true > v := <a,b,c>; 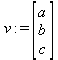 > BasisFormat(true);false > v;aer + bеφ +ceθ > SetCoordinates(polar);polar > MapToBasis(<r,theta>, 'cartesian');r cos(θ)ex + r sin(θ)ey > SetCoordinates(spherical);spherical > MapToBasis(<r,phi,theta>, 'cartesian');r sin(φ)cos(θ)ex + r sin(φ)sin(θ)ey + r cos(φ)еz > SetCoordinates(spherical[r,phi,theta]);sphericalr,φ,θ > MapToBasis(VectorField(<r,0,0>), 'cartesian'[x,y,z]);хēх + yēy + zēz Пакет VectorCalculus предусматривает возможность задания новой системы координат с помощью команды: AddCoordinates(newsys, eqns, owrite) где newsys — спецификация новой системы координат в виде symbol[name, name, …]; eqns — соотношения между координатами новой системы и прямоугольной системы координат, представленные в виде list(algebraic); owrite — заданное опционально равенство. 4.11.3. Основные операции с векторамиВ данном пакете переопределены некоторые основные операции над векторами. Прежде всего, это операции сложения (+) и скалярного умножения (*), которые поясняются следующими примерами (файл vop) : > SetCoordinates(cartesian);cartesian > <x,y,z> + m*<x1,y1,f1>;(x + m x1)ex + (у + m y1)ey + (z + m f1)ez > (<r(a+h),s(a+h),t(a+h)> - <r(a),s(a),t (a)>) / h; 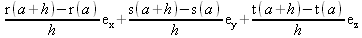 > limit(%,h=0);D(r)(a)ex + D(s)(a)ey + D(t)(a)ez Обратите внимание на вычисление предела в конце этих примеров. Далее можно отметить операцию точечного умножения, которая иллюстрируется следующими вполне очевидными примерами: > <a,b> . <c,d>;ac+bd > SetCoordinates(polar);polar > <a,b> . <c,d>;a cos(b) c cos(d) +a sin(b) c sin(d) > combine(%,trig);a c cos(b-d) > SetCoordinates(cartesian[x,y,z]);cartesianx, y, z > Del . VectorField(<х^2,у^2,z^2>);2x +2y + 2z > Del . Del;VectorCalculus: - Laplasian > (Del . Del) (f(x,y,z)); 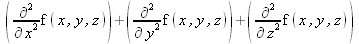 > L := VectorField( <x,y,z> ) . Del;L:= e→vectorCalculus:-`.`(Vector[column](3,[...],datatype = anything, storage = rectangular, order = Fortran_order, attributes = [vectorfield, coords = cartesian[x,y,z]], shape = [],)VectorCalculus:-Del(e)) > L(f(x,y,z)); 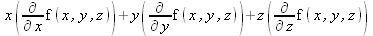 Определена также операция кросс-умножения: > <a,b,c> &х <d,e,f>;(bf - ce)ex + (cd - af)ey +(ae - bd)ez > SetCoordinates(cylindrical);cylindrical > <a,b,c> &x <d,e,f>; 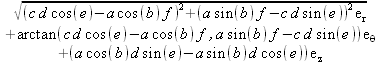 > SetCoordinates(cartesian[x,y,2]);cartesianx, y, z > Del &x VectorField( <y,-x,z> );(-2)ēz > L := VectorField(<x,y,z>) &x Del;L: = e→vectorCalculus:-`&x`(Vector[column](3,[...],datatype = anything, storage = rectangular, order = Fortran_order, attributes = [vectorfield, coords = cartesian[x, y,z]], shape = []), VectorCalculus:-Gradient(e)) > L(f(x,y,2)); 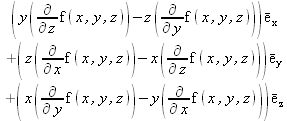 > L := Del &x Del;L := (VectorCalculus:-Curl) @ (VectorCalculus:-Gradient) > L(f(x,y,z));0ēx 4.11.4. Операции с кривымиВ пакете векторных операций определен ряд типовых операций с кривыми. Ниже представлено задание эллиптической кривой и вычисление в аналитической форме нормали и радиуса кривизны (файл vopcurves): > SetCoordinates(cartesian);cartesian > assume(t::real); > ell := <2*cos(t),sin(t)>;ell := 2 cos(t)ex + sin(t)ey > nv := simplify(PrincipalNormal(ell,t));  > len := simplify(LinearAlgebra:-Norm(nv, 2));  > r := simplify(RadiusOfCurvature(ell));  Теперь можно представить саму кривую (эллипс) и ее эволюту (рис. 4.39): > ev := simplify(ell + r * nv / len); 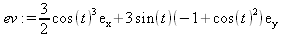 > plot([[ell[1], ell[2], t=0..2*Pi], [ev[1], ev[2], t=0..2*Pi]]);  Рис. 4.39. Графики кривой — эллипса и ее эволюты Нетрудно заметить, что для эллипса эволюта представляет собой удлиненную астроиду. Для вычисления кривизны кривой С используется функция Curvature(C, t) в которой параметр t может и отсутствовать: > Curvature(<cos(t),t,sin(t)>, t); 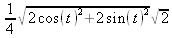 > с := Curvature(t -> <t,t^2,t^4>): > simplify(c(t)) assuming t::real; 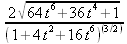 > SetCoordinates('polar');polar > Curvature(<exp(-t^2), t>): > simplify(%) assuming t::real; 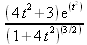 4.11.5. Интегрирование в пакете VectorCalculusВ аспекте практических приложений векторного анализа и теории поля особый интерес представляют приложения интегрирования пакете VectorCalculus. Так, видоизмененная функция int(f, dom) задает вычисление интеграла от функции f по области dom, например (файл vecint): > restart:with(VectorCalculus): > int(х^2+у^2, [x,y] = Circle(<0,1>, r)); 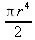 > int(sin(х)*cos(у)*tan(z), [x,y,z] = Parallelepiped(0..Pi, 0..Pi/3, 0..Pi/4));½√3 ln(2) Функция PathInt(f, dom) вычисляет интеграл пути для функции f с Rn до R: > PathInt(х^2, [х,y] = Line(<0,0>, <1,2>)); 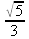 > PathInt(х^2+y^2, [х,y] = Circle(<0,0>, 3/2)); 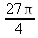 > PathInt(1, [х,y] = Ellipse(х^2+y^2/2-1));  Другая функция LineInt(F, dom), где F — вектор или процедура задания векторного поля, dom — параметр, характеризующий направление интегрирования, задает вычисление линейного интеграла в пространстве Rn: > SetCoordinates(cartesian[х,y]);cartesianx, у > LineInt(VectorField(<х,y>), Line(<0,1>, <2,-5>));14 > LineInt(VectorField(<y,-х>), Circlet<0,0>, r));-2 r² π > LineInt(VectorField(<y,-х>), Ellipse(х^2/4+y^2/9-1));-12π > LineInt(VectorField(<y,-х>), Arc(Ellipse(х^2/4+у^2/9-1), 0, Pi/2));-3π Функция ArcLength(C,dom) задает вычисление длины дуги С по известному интегральному выражению для нее: > ArcLength(<r*cos(t),r*sin(t)>, t=0..Pi) assuming r>0;πr > ArcLength(t -> <t,t^2>, 0..2);√17-¼ln(-4+√17) > evalf(%);4.646783762 Рекомендуется просмотреть различные варианты задания области интегрирования dom в справке по этому пакету. 4.11.6. Задание матриц специального типаПакет VectorCalculus позволяет для заданной функции f задавать несколько матриц специального вида, которые часто используются при решении задач теории поля: Hessian(f, t) — создание матрицы гессиана; Jacobian(f, v, det) — создание матрицы якобиана; Wronskian(f, t) — создание матрицы вронскиана. Примеры задания таких матриц приведены ниже (файл vecmatrix): > Hessian(ехр(х*y), [х,y]); 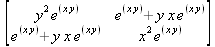 > Hessian(а/(х^2+y^2+z^2), [х, y, z]); 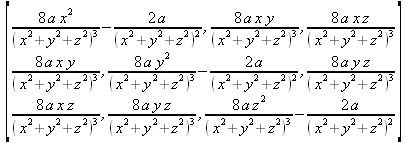 > Н := unapply(%, [a,x,y,z]): > Н(1/2, 0.3, 0.7, 0.1); 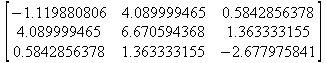 > Jacobian([r*cos(t), r*sin(t)], [r,t]); 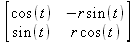 > Jacobian([r*cos(t), r*sin(t)], [r,t], 'determinant'); 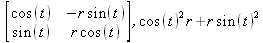 > Wronskian([exp(t),ln(t),sin(t)], t); 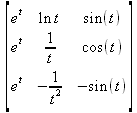 > Wronskian([t, t^2, t^3], t) 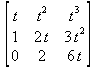 4.11.7. Функции теории поляК основным функциям теории поля относятся: Curl(F) — вычисляет вихрь векторного поля в R³; Divergence(F) — вычисляет дивергенцию векторного поля; Flux(f, dom) — вычисляет поток векторного поля в R³; Gradient(f, с) — вычисляет градиент функции f в пространстве от Rn до R; Del(f, с) и Nabla(f, с) — векторные дифференциальные операторы; Laplacian(f, с) или Laplacian(F) — вычисляет лапласиан функции f или векторного определения (процедуры) F; ScalarPotential(v) — вычисляет скалярный потенциал векторного поля; Torsion(C, t) — вычисляет торсион в R³; VectorPotential(v) — вычисляет векторный потенциал в R³; Довольно громоздкие определения этих функций, основанные на использовании криволинейных и поверхностных интегралов, имеются в учебной литературе. Не приводя их, ограничимся приведенными ниже примерами применение указанных выше функций (файл vecft): > restart:with(VectorCalculus): SetCoordinates('cartesian'[x,y,z]);cartesianx, у, z > F := VectorField( <-y,x,0> );F:=-yēx +хēу > Curl(F);2ēz > Del &x F;2ēz > Nabla &x F;2ē > CrossProduct(Del, F);2ēz > F := VectorField(<х^2,y^2,z^2>);F:=-x²ēх + y²ēу + z²ēz > Divergence(F);2х + 2у + 2z > Flux(VectorField(<x,y,z>, cartesian[x,y,z]), Sphere(<0,0,0>, r));4r³ π > Gradient(х^3/3+у^2, [x,y]);x²ēx + 2yēу 0ēх > Del(х^2+у^2+z^2);2xēx + 2уēу + 2zēz > Nabla(х^2+у^2+z^2);2xēx + 2уēу + 2zēz > Del . %;6 > Laplacian(х^2+у^2+z^2, [x,y,z]);6 > Laplacian(f(r,theta,z)); 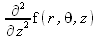 > SetCoordinates('cylindrical' [r, theta, z])cylindricalr, θ, z > Laplacian(f(r, theta, z)); 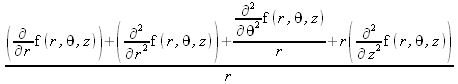 > SetCoordinates('cartesian'[x,y,z]);cartesianx, y, z > v := VectorField(<x,y,-z>);v := xēx + уēу - zēz > ScalarPotential(v); 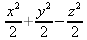 > v := VectorField(<-y,0,z>);v := -yēx + zēz > ScalarPotential(v); den := х^2 + y^2 + z^2;den := x² + y² + z² > ScalarPotential((x,y,z) -> <x,y,z>/den);(x,y,z)→½ ln(x² + y² + z²) > SetCoordinates('spherical'[r,phi,theta]);sphericalr, φ, θ > v := VectorField(<r,0,0>);v:= r ēг > ScalarPotential(v); 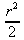 > restart:with(VectorCalculus): simplify( Torsion(<t,t^2,t^3>)) assuming t::real; 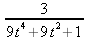 > Torsion(t -> <2*t,sin(t),cos(t)>);  > SetCoordinates('cartesian'[x,y,z]); v := VectorField(<y,-x,0>);cartesianx, y, z v:= уēx - хēу > VectorPotential(v);-xzēx - yzēу > SetCoordinates('cylindrical'[r,theta,z]);cylindricalr, θ, z > v := VectorField(<r,0,-2*z>);v:= rēr -2zēz > VectorPotential(v);(-r sin(θ)² z - r cos(θ)² z) ēθ > simplify(Curl(%));rēr - 2zēz Обратите внимание на то, что для гарантии правильного выполнения этих команд и отсутствия «зависания» компьютера может потребоваться команда restart и перезагрузка пакета VectorCalculus. 4.11.8. Приближение площади сложной поверхности суммами РиманаОдним из важнейших приложений пакета VectorCalculus является вычисление длин дуг и площадей сложных поверхностей на основе применения линейных и поверхностных интегралов. Иногда это встречает большие трудности и требует специальных подходов. Примером может служить поверхность, заданная рис. 4.40. Эта поверхность построена с имитацией ее освещения от внешнего источника света.  Рис. 4.40 Сложная поверхность с эффектами ее освещения внешним источником света Применим обычную процедуру вычисления площади поверхности. Для этого вычислим для нее матрицу якобиана и удалим из нее столбец с нулевыми элементами (файл vecrim): > J := Jacobian(f, [х, у, z]); 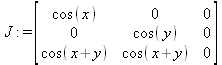 > J := DeleteColumn(J, [3]); 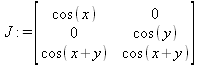 Тогда площадь поверхности вычисляется следующим образом: 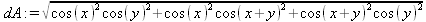 > Int(Int(dA, x=0..2*Pi), y=0..2*Pi); 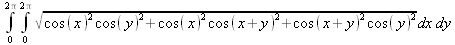 К сожалению, этот двойной интеграл Maple не вычисляет из-за сложности подынтегрального выражения, график которого представлен на рис. 4.41.  Рис. 4.41. График подынтегрального выражения Для приближенного вычисления площади можно разбить поверхность на достаточное число сегментов и использовать замену интегралов суммами Римана. Оценка нижней и верхней сумм Римана для четверти поверхности (ее одного квадранта) представлена ниже: > for s from 1 to 8 do F := (k, t)->subs({x=k*Pi/(10*s), y=t*Pi/(10*s)}, dA): A||s := evalf((Pi/<10*s))^2*sum(sum(F(p, q), p=0..10*s-1), q=0..10*s-1)): print(A||s); end do:7.408455387 7.429353779 7.429810700 7.429973244 7.430045037 7.430081583 7.430102033 > for s from 1 to 8 do F := (k, t)->subs({x=k*Pi/(10*s), y=t*Pi/(10*s)}, dA): Alls := evalf((Pi/(10*s))^2*sum(sum(F(p, q), p=1..10*s), q=1..10*s)): print(A||s) end do:7.408455386 7.427471278 7.429353778 7.429810700 7.429973260 7.430045062 7.430081587 7.430102036 Поскольку эти суммы явно сходятся, то можно считать применение сумм Римана приемлемым и принять, что площадь данной поверхности приближенно равна: > Area := 4*7.43;Area:= 29.72 4.11.9. Вычисление поверхностных интеграловПриведенный выше пример иллюстрирует трудности вычислений поверхностных интегралов. Разумеется, далеко не всегда Maple требует специальных подходов к вычислению подобных интегралов и многие из них благополучно вычисляются. Для этого используется функция: SurfaceInt(f, dom, inert) где f — алгебраическое выражение, задающее интегрируемую зависимость, dom — спецификация поверхности в виде list(name)=surface и inert — имя, задаваемое как опция. Примеры применения данной функции представлены ниже (файл surint): > with(VectorCalculus): > SurfaceInt(1, [x,y,z] = Surface(<r,s,t>, s=0..Pi/2, t=0..Pi, coords=spherical)) assuming r>0;π r² >SurfaceInt(x+y+z, [x,y,z] = Surface(<s,t,4-2*s-t>, [s,t] = Triangle(<0.0>,<1,0>,<1,1>))); 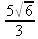 > SurfaceInt(2*y^2, [x,y,z] = Sphere(<0,0,0>, r)); 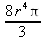 |
|
||||||
| Главная | В избранное | Наш E-MAIL | Добавить материал | Нашёл ошибку | Наверх | ||||||||
|
|
||||||||

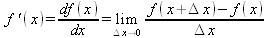 (4.1)
(4.1)