|
||||
|
|
Глава 5Анализ функциональных зависимостей и обработка данных Аналитические функции и степенные многочлены (полиномы) широко используются в математике и физике. В этой главе описана работа с функциями и полиномами, включающая в себя традиционный анализ функций, выявляющий их особенности и обеспечивающий различные преобразования функций, вычисление и преобразование полиномов в том числе ортогональных и техника приближения (аппроксимации) функций и табличных данных полиномами и сплайнами. Все эти вопросы имеют исключительно важное значение в практике научно-технических расчетов. 5.1. Анализ функциональных зависимостей5.1.1. Понятие о функциональных зависимостяхГоворят, что y(x) есть функция, если известно правило, согласно которому каждому значению аргумента x соответствует некоторое значение у. Мы уже сталкивались с элементарными и специальными математическими функциями, которые имеют свои уникальные имена. Возможны и функции двух и более переменных, например функции Бесселя разного порядка. Здесь мы под функциональной зависимостью будем понимать не только зависимости, заданные отдельными элементарными или специальными функциями, но и любые зависимости какой либо величины от ряда других величин — переменных. Такие выражения могут содержать ряд элементарных или специальных математических функций. Например, sin(x) и cos(x) это просто элементарные функции, а f(х)=2*sin(x)*cos(x) это уже функциональная зависимость f от х. Любое математическое выражение, содержащее переменные х, y, z, … можно рассматривать как функциональную зависимость f(x, y, z, …) от этих переменных. Функциональная зависимость или функция f(х) даже от одной переменной может быть достаточно сложной, содержать корни (значения x при которых f(х)=0), полюса (значения х при которых f(х)→∞), максимумы и минимумы, разрывы, асимптотические значения, точки перегиба и т.д. Часто эти особенности видны на графике зависимости f(х), но анализ функциональной зависимости предполагает, что эти особенности могут быть точно идентифицированы и определены по математическому выражению, представляющему зависимость. Например, поиск корней сводится к решению уравнения f(х)=0 в заданном интервале, поиск экстремумов полагает нахождение значений x в точках экстремумов и значений f(х) в них и т.д. К сожалению, пока нет средств, сразу выявляющих все особенности функциональных зависимостей, поскольку даже средства, решающие частные задачи анализа функций, довольно сложны и специфичны. Достаточно отметить проблему поиска экстремумов функций (особенно функций нескольких переменных). Поэтому функции приходится анализировать индивидуально. 5.1.2. Поиск экстремумов функций по нулям первой производнойС помощью функции fsolve системы Maple легко находятся значения независимой переменной x функций вида f(x), при которых f(х)=0 (корни этого уравнения). При этом данная функция позволяет (в отличие от функции solve) изолировать корни функции f(х) указанием примерного интервала их существования. Для простых функций одной переменной f(х) поиск экстремумом часто сводят к нахождению точек, в которых первая производная f(х) обращается в нуль. Для этого можно использовать также функцию fsolve (иногда и solve, но она дает вывод в более сложной форме). Приведем пару примеров (файл extrem): > у:=expand((х-3)*(х-1)*х*(х+2));y := х4 - 2х3 - 5х2 + 6х > dy:=simplify(diff(y,х));dy := 4х³ - 6х² - 10х + 6 > plot({y,dy},х=-3..3,-10..10,color=black,thickness=[2,1]); > extrem:=fsolve(dy=0,х);extrem := -1.302775638, 0.5000000000, 2.302775638 В этом примере создан полином y с корнями 3, 1, 0 и -2 и найдена его производная dy. На рис. 5.1 построены графики функции и ее производной (жирная кривая). Из него видно, что полином p имеет экстремумы в точках, лежащих в промежутках между корневыми точками. Их значения и найдены как значения переменной extrem, для которых вторая производная равна 0. Рекомендуется проверить вид вывода, если fsolve заметить на solve. 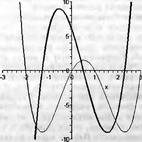 Рис. 5.1. График функциональной зависимости — полинома и ее производной Возьмем еще один пример для поиска экстремумов выражения sin(x)/x. Это выражение имеет бесконечное число экстремумов слева и справа от х=0 (в этой точке расположен главный максимум со значением 1). Ограничимся поиском трех экстремумов в интервале изменения x от 3 до 12: > f:=sin(х)/x:df:=diff(f,x); 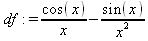 > plot({ f, df},x=0..12,color=black,thickness=[2,1]): > [fsolve(df,x=3..6),fsolve(df,x=7..9),fsolve(df,x=9..12)];[4.493409458, 7.725251837, 10.90412166] Тут уже приходится искать каждый экстремум поодиночке, задавая поиск в соответствующем интервале изменения х. Для просмотра графика функциональной зависимости и ее производной достаточно в конце второй строки ввода заменить знак «:» на «;». 5.1.3. Поиск экстремумов в аналитическом видеФункция solve нередко позволяет найти экстремумы в аналитическом виде как нули первой производной. Приведем примеры этого (файл extrem): > restart:y:=ехр(-а*х)-exp(-b*x);dy:=diff(y,х);у = e(-ax) - е(-bx) dy := -ae(-ax) + bе(-bх) > solve(dy,x); 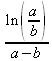 > restart:y:=а*х*ехр(-b*x);dy:=diff(y,х);y := axe(-bx) dy := ae(-bx) - axbe(-bx) > solve(dy,x); 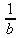 Этот метод иногда можно распространить на случай ряда переменных. Ниже представлен такой пример для функции двух переменных: > restart: > z:=(х,y)-> а*х^2 + b*х*y + с*y^2 + d*(х-y);z := (х,у)→aх² + bху + су² + d(x-y) > xy:=solve({diff(z(x,y),x) = 0, diff(z(x,y),y) = 0},{х,y}); 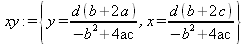 > z(rhs(xy[2]),rhs(xy[1])); 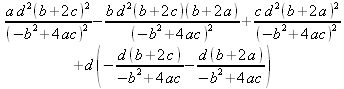 > simplify(%); 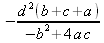 Разумеется, подобное решение возможно далеко не всегда, хотя и частные решения данной задачи представляют значительный практический интерес. 5.1.4. Поиск максимума амплитудно-частотной характеристикиОдной из практически важных задач может служить нахождение пика амплитудно-частотной характеристики слабо демпфированной системы с массой m и частотой собственных колебаний ω0. Эту характеристику можно представить следующим известным выражением (файл afc): > restart; > A:=A0/sqrt(m^2* (omega0^2-omega^2)^2+gamma^2*omega^2); 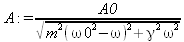 Найдя ее производную и, вычислив корни последней, получим: > dA:=diff(A,omega); 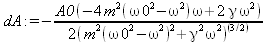 > ss:=solve(dA=0,omega); 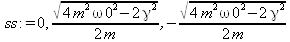 Из этих трех частот только одна физически реальна — средняя. Остальные могут быть отброшены. А теперь приведем пример с конкретными числовыми данными: > AA:=subs(А0=5,omega0=10,m=1, gamma=1, А); 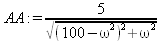 > AAprime :=diff(АА, omega); 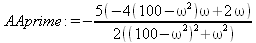 > ss1:=solve(AAprime=0,omega); 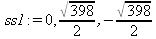 > evalf(ss1);0., 9.974968670 , -9.974968670 Нетрудно подметить, что частота пика амплитудно-частотной характеристики чуть меньше частоты собственных колебаний системы. 5.1.5. Поиск экстремумов с помощью функции extremaРяд функций служит специально для вычисления экстремумов, максимумов и минимумов функций, а также для определения их непрерывности. Одна из таких функций extrema позволяет найти экстремумы выражения expr (как максимумы, так и минимумы) при ограничениях constrs и переменных vars, по которым ищется экстремум: extrema(expr, constrs) extrema(expr, constrs, vars) extrema(expr, constrs, vars, 's') Ограничения contrs и переменные vars могут задаваться одиночными объектами или списками ряда ограничений и переменных. Найденные координаты точки экстремума присваиваются переменной 's'. При отсутствии ограничений в виде равенств или неравенств вместо них записывается пустой список {}. Эта функция в предшествующих версиях Maple находилась в стандартной библиотеке и вызывалась командой readlib(extrema). Но начиная с Maple 7 ее можно использовать без предварительного объявления. В этом убеждают приведенные ниже примеры (файл extrema): > restart: > z:=(х,y)-> а*х^2 + b*x*y + с*y^2 + d*(х-y);z:= (х,у)→ах² + bxy + су² + d(х - y) > extrema(z(х,y),{},{х,y},'s'); 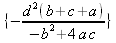 > s; 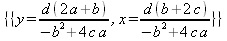 > extrema(а*х^2+b*х+с,{},x,'s');s; 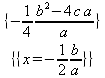 > extrema(х*ехр(-х),{}, х, 's'); s;{e(-1)} {{x = 1}} > extrema(sin(x)^2,{},x,'s');s;{0,1} {{x=0}, {х=½π}} > extrema(х+у/z,х^2+у^2+z^2=1,{x,y,z},'s');s;{max(1 - RootOf(_Z4 + 1)2, - 1 + RootOf(_Z4 + 1)2), min(1 - RootOf(_Z4 + 1)2, -1 + RootOf(_Z4 + 1)2)} {{z = RootOf(_ Z4 + 1), x = -1, у = RootOf(_Z4 + 1)3}, {x = 1, z = RootOf(_ Z4 + 1), у = - RootOf(_ Z4 + 1)3}} > evalf(%);{{x = -1., у = -0.7071067812+0.7071067812 I, z = 0.7071067812+0.7071067812 I}, {z = 0.7071067812+0.7071067812 I, x = 1., у = 0.7071067812-0.7071067812 I}} Как видно из приведенных примеров, функция extrema возвращает как значения экстремумов, так и значения аргументов, при которых экстремумы наблюдаются. Обратите внимание, что в первом примере результат вычисления экстремума функции z(x,y) оказался тем же, что и в предшествующем разделе. Это говорит в пользу применения функции extrema. Для проверки оптимизационных алгоритмов существует ряд тестовых функций. Одна из таких функций — функция двух переменных Розенброка. В представленном ниже примере она задана как rf(x,y): > rf:= (x,у)->100*(у-х^2)^2+(1-х)^2;rf:=(x,.y)→100(y-x²)²+(1-x)² > extrema(rf(х,у),{х,у},'s');s;{{y = -RootOf f(_ Z4 + 1)3, х = 1, z = RootOf(_Z4 + 1)}, {x = -1, у = RootOf(_Z4 + 1)3, z = RootOf(_Z4 + 1)}} > evalf(%);{{y = 0.7071067812-0.7071067812, x = 1., z =0.7071067812+0.7071067812 I}, {z = 0.7071067812+0.7071067812 I, x = -1.,y = -0.7071067812+0.7071067812 I}} Как нетрудно заметить, минимум этой функции при значениях x=у=1, равный 0, функцией extrema явно не обнаружен. Однако это не недостаток данной функции, а просто неудачное ее применение. Функция Розенброка имеет минимум значения и для его обнаружения надо использовать функцию minimize, описанную ниже. Функция extrema дает неплохие результаты при поиске экстремумов простых аналитических функций, не имеющих особенностей. Однако при анализе сложных функций, содержащих функции со сравнением аргумента (например, abs(x), signum(x) и др.) функция extrema часто отказывается работать и просто повторяет запись обращения к ней. 5.1.6. Поиск минимумов и максимумов аналитических функцийЧасто нужно найти минимум или максимум заданной функции. Для поиска минимумов и максимумов выражений (функций) expr служат функции стандартной библиотеки: minimize(expr, opt1, opt2, ..., optn) maximize(expr, opt1, opt2, ..., optn) Эти функции могут разыскивать максимумы и минимумы для функций как одной, так и нескольких переменных. С помощью опций opt1, opt2, …, optn можно указывать дополнительные данные для поиска. Например, параметр 'infinity' означает, что поиск минимума или максимума выполняется по всей числовой оси, а параметр location (или location=true) дает расширенный вывод результатов поиска — выдается не только значение минимума (или максимума), но и значения переменных в этой точке. Примеры применения функции minimize приведены ниже (файл minmax): > minimize(х^2-3*х+y^2+3*y+3); 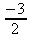 > minimize(х^2-3*х+y^2+3*y+3, location); 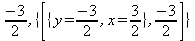 > minimize(х^2-3*х+y^2+3*y+3, х=2..4, y=-4..-2, location);-1, {[{х = 1, y = -2}, -1]} > minimize(х^2+y^2,х=-10..10,y=-10..10);0 > minimize(х^2 + y^2,х=-10..10,y=-10..10, location);0, {[y = 0, х = 0},0]} > minimize(abs(х*ехр(-х^2)-1/2), х=-4..4);½-½√2 е(-1/2) > minimize(abs(х*ехр(-х^2)-1/2), х=-4..4, location=true); 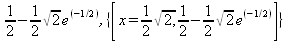 Приведем подобные примеры и для функции поиска максимума — maximize: > maximize(х*ехр(-х));е(-1) > maximize(х*ехр(-х),location);е(-1), {[{х=1}, е(-1)] } > maximize(sin(х)/х,х=-2..2,location);1, {[{x=0}, 1]} > maximize(exp(-х)*sin(y),х=-10..10,y=-10..10, location); 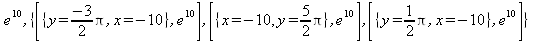 Обратите внимание на то, что в предпоследнем примере Maple 9.5 выдал верный результат, тогда как Maple 8 в этом примере явно «оскандалился» и вместо максимума функции sin(x)/x, равного 1 при x=0, выдал результат в виде бесконечности: ∞, {[{x =0}, ∞]}Эта ситуация кажется более чем странной, если учесть, что в этом примере еще Maple 6 давал правильный результат. Это еще один пример, показывающий, что в отдельных случаях Maple может давать неверные результаты. Применим функцию minimize для поиска минимума тестовой функции Розенброка. Рис. 5.2 показывает, что minimize прекрасно справляется с данной задачей. На рис. 5.2 представлено также построение функции Розенброка, хорошо иллюстрирующее ее особенности. 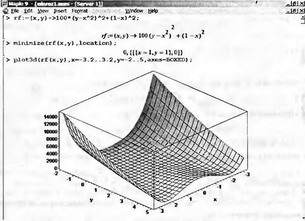 Рис. 5.2. Поиск минимума функции Розенброка и построение ее графика Трудность поиска минимума функции Розенброка связана с ее характерными особенностями. Из рис. 5.2 видно, что эта функция представляет собой поверхность типа «глубокого оврага с почти плоским дном», в котором и расположена точка минимума. Такая особенность этой функции существенно затрудняет поиск минимума. То, что система Maple 9.5 справляется с данной тестовой функцией, вовсе не означает, что трудности в поиске минимума или максимума других функций остаются позади. 5.1.7. Поиск минимума функций с ограничениями методом выпуклого программированияЧасто необходимо найти минимум некоторой функции при наличии ограничений на значения независимых переменных. Ниже рассматривается нетривиальная задача такого рода, решаемая методом выпуклого программирования (разновидность нелинейного программирования) — файл minp. Пусть надо найти минимум функции f:=х1^2+(х2–1)^2 при следующих ограничениях: 2x1+х2>=7, x1+2*х2>=5, x1>=0 и х2>=0. Составим на основе этого функцию Лагранжа: > F:=x1^2+(х2-1)^2+y1*(7-2*х1-х2)+y2*(5-х1-2*х2);F:= x1² + (х2-1)² + у1(7-2х1-х2) + у2(5-х1-2х2) и найдем ее частные производные: > F1:=diff(F,x1);F1:=2x1-2y1-y2 > F2:=diff(F,x2);F2:=2x2 -2-y1-2y2 > F3:=dxff(F,y1);F3:=7-2x1-x2 > F4:=diff(F,y2);F4:=5-x1-2x2 Соберем воедино все равенства и неравенства этой задачи: > eq:={Fl=u1,F2=u2,x1*F1,x2*F2,F3+v1,F4+v2,y1*F3,y2*F4, x1>=0,x2>=0,y1>=0,y2>=0,u1>=0,u2>=0,v1>=0,v2>=0};eq := {2x1-2y1-y2=u1, 2x2-2-y1-2y2=u2, 7-2x1-x2+v1, 5-x1-2x2+v2, y1(7-2x1-x2), y2(5-x1-2x2), x1(2x1-2y1-y2), x2(2x2-2-y1-2y2), 0≤x1, 0≤x2, 0≤y1, 0≤y2,0≤u1,0≤v1, 0≤v2, 0≤u2} Первые шесть равенств соответствуют теореме Куна-Такера о том, что в точке минимума существуют целые неотрицательные числа u1, u2, v1 и v2 для которых выполняются эти шесть равенств (обратите внимание на то, что запись только левой части равенства означает, что она приравнивается к 0). Теперь с помощью функции solve можно найти решение данной задачи: > solve(eq,{x1,х2,y1,y2,u1,u2,v1,v2}); 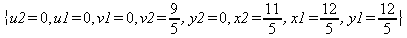 Таким образом, на указанном множестве функция достигает минимума в точке (12/5, 11/5). 5.1.8. Анализ функций на непрерывностьДля исследования функций на непрерывность (отсутствие разрывов) Maple имеет функцию iscont, записываемую в ряде форм: iscont(expr, х = а..b) iscont(expr, х = а..b, 'closed') iscont(expr, х = а..b, 'open') Она позволяет исследовать выражение expr, заданное в виде зависимости от переменной х, на непрерывность. Если выражение непрерывно, возвращается логическое значение true, иначе — false. Возможен также результат типа FAIL. Параметр 'closed' показывает, что конечные точки должны также проверяться, а указанный по умолчанию параметр 'open' — что они не должны проверяться. Работу функции iscont иллюстрируют следующие примеры (файл fanal): > iscont(1/х^2,х=-1..1);false > iscont(1/х^2,х=-1..1,'closed');false > iscont(1/x,х=0..1);true > iscont(1/x,x=0..1,'closed');false > iscont(1/(x+a),x=-1..1);FAIL Рекомендуется внимательно присмотреться к результатам этих примеров и опробовать свои собственные примеры. 5.1.9. Определение точек нарушения непрерывностиФункции, не имеющие непрерывности, доставляют много хлопот при их анализе. Поэтому важным представляется анализ функций на непрерывность. Начиная с Maple 7, функция discont(f,x) позволяет определить точки, в которых нарушается непрерывность функции f(x). Она вычисляет все точки в пределах изменения х от –∞ до +∞. Результаты вычислений могут содержать особые экстрапеременные с именами вида _Zn~ и _NNn~. В частности, они позволяют оценить периодические нарушения непрерывности функций. Примеры применения функции discont приведены ниже (файл fanal): > discont(1/(х-2),х);{2} > discont(1/((х-1)*(х-2)*(х-3)),х);{1, 2, 3} > discont(GAMMA(х/2),х);{-2_NN1~} Весьма рекомендуется наряду с применением данной функции просмотреть график анализируемой функции. Еще раз полезно обратить внимание на то, что в ряде примеров в выводе используются специальные переменные вида _NameN~, где Name — имя переменной и N — ее текущий номер. После выполнения команды restart отсчет N начинается с 1. Если вывод с такими переменными уже применялся, то их текущие номера могут казаться произвольными. Специальные переменные часто используются для упрощения выводимых выражений. 5.1.10. Нахождение сингулярных точек функцииМногие операции, такие как интегрирование и дифференцирование, чувствительны к особенностям функций, в частности, к их разрывам и особым точкам. Напомним, что разрыв характеризуется двумя значениями y(x) в точке разрыва на оси абсцисс xр. Возможны разрывы с устремлением функции к бесконечности с той или иной стороны от точки хр. Функции могут иметь один разрыв или конечное число разрывов. Функция singular(expr, vars) позволяет найти особые (сингулярные) точки выражения expr, в которых она испытывает разрывы. Дополнительно в числе параметров может указываться необязательный список переменных. Примеры применения этой функции приведены ниже (файл fanal): > singular(ln(х)/(x^2-a));{а = а, х = 0}, {а = x², x = x} > singular(tan(х));{x = _Z22~ π + ½π} > singular(1/sin(х));{x=π_Z21~} > singular(Psi(х*y),{х,y}); 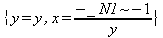 > singular(x+y+1/x,{х,у});{у=у, x=0}, {у=у, x=-∞}, {y=∞, x=x}, {y=–∞, x=x}, {x=∞,y=y} 5.1.11. Вычисление асимптотических и иных разложенийВажным достоинством системы Maple является наличие в ней ряда функций, позволяющих выполнять детальный анализ функций. К такому анализу относится вычисление асимптотических разложений функций, которые представляются в виде рядов (не обязательно с целыми показателями степени). Для этого используются следующая функция: asympt(f,x) asympt(f,х,n) Здесь f — функция переменной х или алгебраическое выражение; х — имя переменной, по которой производится разложение; n — положительное целое число (порядок разложения, по умолчанию равный 6). Ниже представлены примеры применения этой функции (файл fanal): > asympt(х/(1-х^2),х); 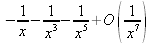 > asympt(n!,n,3); 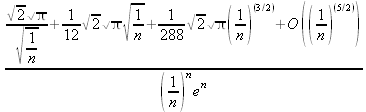 > asympt(exp(x^2)*(1-exp(x)), x); 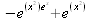 > asympt(sqrt(Pi/2)*BesselJ(0,x), x, 3); 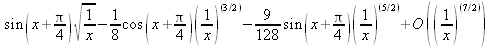 5.1.12. Пример анализа сложной функцииНиже мы рассмотрим типичный анализ достаточно «сложной» функции, имеющей в интересующем нас интервале изменения аргумента х от -4 до 4 нули, максимумы и минимумы. Определение функции f(x), ее графики и график производной df(x)/dx даны на рис. 5.3. Этот рисунок является началом полного документа, описываемого далее (файл analizf). 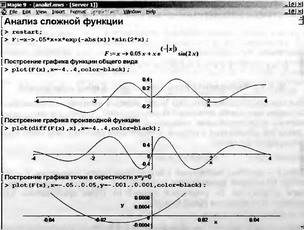 Рис. 5.3. Задание функции F(x) и построение графиков функции и ее производной Функция F(x), на первый взгляд, имеет не совсем обычное поведение вблизи начала координат (точки с х=у=0). Для выяснения такого поведения разумно построить график функции при малых x и у. Он также представлен на рис. 5.2 (нижний график) и наглядно показывает, что экстремум вблизи точки (0,0) является обычным минимумом, немного смешенным вниз и влево от начала координат. Теперь перейдем к анализу функции F(x). Для поиска нулей функции (точек пересечения оси х) удобно использовать функцию fsolve, поскольку она позволяет задавать область изменения х, внутри которой находится корень. Как видно из приведенных ниже примеров, анализ корней F(x) не вызвал никаких трудностей, и все корни были уточнены сразу: > fsolve(F(х),х,-2...-1);-1.462069476 > fsolve(F(x),х,-.01..0.01);0. > fsolve(F(х),х,-.05..0);-.02566109292 > fsolve(F(x),х,1..2);1.710986355 > fsolve(F(x),x,2.5..3);2.714104921 Нетрудно заметить, что функция имеет два очень близких (но различных) корня при x близких к нулю. Анализ функции на непрерывность, наличие ее нарушений и сингулярных точек реализуется следующим образом: > iscont(F(x),x=-4..4);true > discont(F(x),x);{ } > singular(F(x));{x = ∞}, {x = -} Этот анализ не выявляет у заданной функции каких-либо особенностей. Однако это не является поводом для благодушия — попытка найти экстремумы F(x) с помощью функции extrema и минимумы с помощью функции minimize завершаются полным крахом: > extrema(F(x),{},х,'s');s;s > minimize(F(х),х=-.1...1);minimize( .05x +xe(-|x|) sin(2x), x=-.1..1) > minimize(F(x),x=-2.5..-2);minimize(.05x + xe(-|x|) sin(2x), x = -2.5 .. -2) Приходится признать, что в данном случае система Maple ведет себя далеко не самым лучшим способом. Чтобы довести анализ F(x) до конца, придется вновь вспомнить, что у функции без особенностей максимумы и минимумы наблюдаются в точках, где производная меняет знак и проходит через нулевое значение. Таким образом, мы можем найти минимумы и максимумы по критерию равенства производной нулю. В данном случае это приводит к успеху: > fsolve(diff(F(х),х)=0,х,-.5.. .5);-.01274428224 > xm:=%;xm:=-.0003165288799 > [F(xm),F(xm+.001),F(xm-.001)];[-.00001562612637, .00003510718293, -.00006236451216] > fsolve(diff(F(x),x)=0,x,-2.5..-2);-2.271212360 > fsolve(diff(F(x),x)=0,x, 2..2.5);2.175344371 Для случая поиска максимумов: > maximize(F(х),х=-1..-.5);maximize( .05 x + xe(-x|) sin(2 x), x =-1..-.5) > fsolve(diff(F(x), x), x,-1.. -.5);-.8094838517 > fsolve(diff(F(x),x),x,.5..2);.8602002115 > fsolve(diff(F(x),x),x, -4..-3);-3.629879137 > fsolve(diff(F(x), x), x, 3..4); Итак, все основные особые точки данной функции (нули, минимумы и максимумы) найдены, хотя и не без трудностей и не всегда с применением специально предназначенных для такого поиска функций. 5.1.13. Maplet-инструмент по анализу функциональных зависимостейДля анализа функциональных зависимостей Maple 9.5 имеет специальный Maplet-Инструмент. Он вызывается командой Tools→Tutors→Calculus-Single Variable→Curve Analysis…. Она открывает окно инструмента, показанное на рис. 5.4. 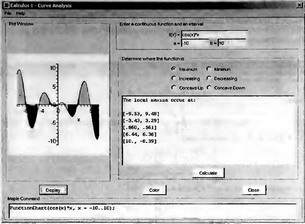 Рис. 5.4. Окно Maplet-инструмента анализа функциональных зависимостей В верхней правой части окна имеются панели для ввода функциональной зависимости f(x) и границ а и b изменения аргумента х. Под ними имеется набор опций для задания того или иного параметра кривой, например ее максимумов Maximum, минимумов Minimum и др. После нажатия клавиши Calculate вычисляются координаты характерных точек или области определения тех или иных особенностей кривой. График анализируемой кривой появляется в левой части окна. В нем строятся точки корней, перегибов и экстремумов зависимости. Цветом выделяются участки, на которых зависимость нарастает или падает. Кнопка Display порождает запись команды, которая строит полученный рисунок. 5.2. Работа с функциями из отдельных кусков5.2.1. Создание функций из отдельных кусковДля создания функций, составленных из отдельных кусков — кусочных функций, Maple 9.5 располагает интересной и по своему уникальной функцией: piecewise(cond_1,f_1, cond_2,f_2, ..., cond_n,f_n, f_otherwise) где f_i — выражение, cond_i — логическое выражение, f_otherwise — необязательное дополнительное выражение. В зависимости от того или иного условия эта функция позволяет формировать соответствующую аналитическую зависимость. К кусочным функциям (подчас в скрытой форме) приводят функции с элементами сравнения аргумента, например abs, signum, max и др. Поэтому в Maple 8 введен достаточно мощный аппарат обработки и преобразований таких функций по частям. 5.2.2. Простые примеры применения функции piecewiseРис. 5.5 показывает задание функции f(х), содержащей три характерных участка. По определенной через функцию пользователя зависимости f(х) можно, как обычно, построить ее график.  Рис. 5.5. Пример задания и применения функции, составленной из отдельных кусков Важно отметить, что созданная с помощью функции piecewise зависимость может участвовать в различных преобразованиях. Например, на рис. 5.3 показано, что она легко дифференцируется и интегрируется, так что можно построить графики производной этой функции и ее интегрального значения. При этом каждая часть функции обрабатывается отдельно. 5.2.3. Работа с функциями piecewiseС функциями типа piecewise можно работать как с обычными функциями. При этом необходимые операции и преобразования осуществляются для каждой из частей функции и возвращаются в наглядной форме. Ниже приведен пример задания функции f в аналитической форме (файл piecewi): > restart; > f := max(х^2 - 2, x-1);f := max(x²-2, x-1) Для выявления характера функции воспользуемся функцией convert и создадим объект g в виде кусочной функции: > g := convert(f, piecewise); 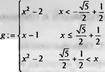 Выполним дифференцирование и интегрирование функции: > fprime := diff(f, х); 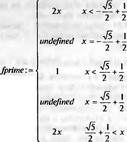 > Int(g,х)=int(g,х); 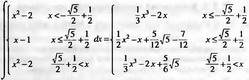 Как нетрудно заметить, результаты получены также в виде кусочных функций. Можно продолжить работу с функцией f и выполнить ее разложение в степенной ряд: > series(f, х);-1+x+O(x6) Чтобы убрать член с остаточной погрешностью, можно выполнить эту операцию следующим образом: > series(g, х);-1+х Обратите внимание на то, что поскольку разложение в ряд ищется (по умолчанию) в окрестности точки х=0, то при этом используется только тот кусок функции, в котором расположена эта точка. 5.3. Операции с полиномами5.3.1. Определение полиномовК числу наиболее известных и изученных аналитических функций относятся степенные многочлены — полиномы. Графики полиномов описывают огромное разнообразие кривых на плоскости. Кроме того, возможны рациональные полиномиальные выражения в виде отношения полиномов. Таким образом, круг объектов, которые могут быть представлены полиномами, достаточно обширен, и полиномиальные преобразования широко используются на практике, в частности, для приближенного представления других функций. Под полиномом в СКМ сумма выражений с целыми степенями. Многочлен для ряда переменных — многомерный полином. К одномерным полиномам относятся степенной многочлен р(х) = аn хn + аn-1 xn-1 + ... a1 x + а0,а также отдельная переменная х и константа. Большое достоинство полиномов состоит в том, что они дают единообразное представление многих зависимостей и для своего вычисления требуют только арифметических операций (их число значительно сокращается при использовании хорошо известной схемы Горнера). Производные от полиномов и интегралы с подынтегральными функциями-полиномами легко вычисляются и имеют простой вид. Есть и достаточно простые алгоритмы для вычисления всех (в том числе комплексных) корней полиномов на заданном промежутке. 5.3.2. Выделение коэффициентов полиномовДля выделения коэффициентов полиномов в Maple служат следующие функции: coeff(p, х) — возвращает коэффициент при х полинома p; coeff(p, x, n) — возвращает коэффициент для члена со степенью n полинома p; coeff(p, x^n) — возвращает коэффициенты при x^n полинома p; coeffs(p, х, 't') — возвращает коэффициенты полинома нескольких переменных, относящиеся к переменной x (или списку переменных) с опцией 't', задающей имя переменной; collect(p, x) — возвращает полином, объединяя коэффициенты при степенях переменной х. Ниже даны примеры применения этих функций (файл coefcoll): > р:=а4*х^4+а3*х^3+а2*х^2+а1*х+а0;р:= а4х4 + a3x3 + а2 х2 + a1 x + а0 > coeff(р,х);а1 > coeff(р,х^3);а3 > coeff(р,х,4);а4 > coeffs(p,x);a0, a4, a1, a3, a2 > q:=x^2+2*y^2+3*x+4*y+5;q:= x² +2 y² + 3x + 4y +5 > coeffs(q);5, 2, 3, 4, 1 > coeffs(q,y);x² +3x +5, 2, 4 > coeffs(q,x,y);5+2y²+4y, 3, 1 > collect(q,x);x² + 2(1,x²,x)² + 3x + (4,4x²,4x)+5 > collect(q,x,y);y(1)x² + y(3)x + y(5+2y²+4у) Дополнительные примеры на применение функции collect можно найти в файле collect. 5.3.3. Оценка коэффициентов полинома по степенямПолином может быть неполным, то есть не содержать членов со степенями ниже некоторой. Функция lcoeff возвращает старший, а функция tcoeff — младший коэффициент полинома нескольких переменных. Эти функции задаются в виде: lcoeff(р) tcoeff(р) lcoeff(р, х) tcoeff(р, х) lcoeff(р, х, 't') tcoeff(р, х, 't') Функции lcoeff и tcoeff возвращают старший (младший) коэффициент полинома р относительно переменной х или ряда переменных при многомерном полиноме. Если х не определено, lcoeff (tcoeff) вычисляет старший (младший) коэффициент относительно всех переменных полинома p. Если третий аргумент t определен, то это имя назначено старшему (младшему) члену p. Если х — единственное неизвестное, и d — степень p по х, то lcoeff(p, x) эквивалентно coeff(p, x, d). Если х — список или множество неизвестных, lcoeff (tcoeff) вычисляет старший (младший) коэффициент p, причем p рассматривается как полином многих переменных. Имейте в виду, что p должен быть разложен по степеням неизвестного x до вызова функций lcoeff или tcoeff. Приведем примеры применения функций lcoeff, tcoeff и coeffs (файл polan): > q:=1/x^2+2/x+3+4*x+5*x^2; 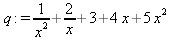 > lcoeff(q,x);5 > lcoeff(q,x,'t');5 > t;x² > coeffs(q,x,'t');3, 1, 4, 2, 5 > t; 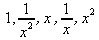 5.3.4. Оценка степеней полиномаФункция degree возвращает высшую степень полинома, a ldegree — низшую степень. Эти функции задаются следующим образом: degree(а,х) ldegree(а, х) Функции degree и ldegree используются, чтобы определить высшую и низшую степень полинома от неизвестного (неизвестных) х, которое чаще всего является единственным, но может быть списком или множеством неизвестных. Полином может иметь отрицательные целые показатели степеней при х. Таким образом, degree и ldegree могут возвратить отрицательное или положительное целое число. Если выражение не является полиномом от x сданным параметром, то возвращается FAIL. Чтобы degree и ldegree возвратили точный результат, полином обязательно должен быть сгруппирован по степеням х. Например, для выражения (x+1)(х+2)-x^2 функция degree не обнаружит аннулирование старшего члена и неправильно возвратит результат 2. Во избежание этой проблемы перед вызовом degree следует применять к полиному функции collect или expand. Если х — множество неизвестных, degree/ldegree вычисляет полную степень. Если х — список неизвестных, degree/ldegree вычисляет векторную степень. Векторная степень определяется следующим образом: degree(р,[]) = 0 degree(р,[x1,х2,...]) = degree(р,x1) degree(lcoeff(р,x1),[х2,...]) Полная степень тогда определяется следующим образом: degree(р, {x1, ...,xn}) = maximum degree(р,{x1,...xn)) или degree(р,{x1,...,xn}) = degree(p,[x1,...,xn]) Обращаем внимание на то, что векторная степень зависит от порядка перечисления неизвестных, а полная степень не зависит. Примеры применения функций degree и ldegree: > restart; > р:=а4*х^4+a3*х^3+а2*х^2;р:=а4 х4 + a3 x3 + а2 х2 > degree(р,х);4 > ldegree(р,х);2 > q:=1/х^2+2/х+3+4*х+5*х^2; 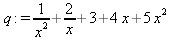 > degree(q,х);2 > ldegree(q,х);-2 > degree(x*sin(x),x);FAIL > zero := y*(x/(x+1)+1/(x+1)-1); 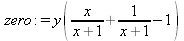 > degree(zero,x);degree(zero, y);FAIL 1 > degree(collect(zero,x,normal),x);degree(collect(zero,y, normal),y);-∞ -∞ 5.3.5. Контроль полинома на наличие несокращаемых множителейДля контроля того, имеет ли полином несокращаемые множители, может использоваться функция irreduc(p) и ее вариант в инертной форме lreduc(p,K), где K — RootOf-выражение. Ниже приведены примеры применения этих тестовых функций: > irreduc(х^2-1);false > irreduc(х^2-2);true > Irreduc(2*x^2+6*x+6) mod 7;false > Irreduc(x^4+x+1) mod 2;true > alias(alpha=RootOf(x^4+x+1)): > Irreduc(х^4+х+1,alpha) mod 2;false 5.3.6. Разложение полинома по степенямДля разложения полинома р по степеням служат инертные функции AFactor(p) и AFactors(p). Полином может быть представлен в виде зависимости от одной или нескольких переменных. Функция Afactor(p) выполняет полную факторизацию (разложение) полинома p от нескольких переменных с коэффициентами в виде алгебраических чисел над полем комплексных чисел. При этом справедливо отношение evala(AFactor(p))= factor(p.complex). Таким образом, эта функция является, по существу, избыточной. В случае одномерного полинома полное разложение на множители является разложением на линейные множители. Функция AFactors аналогична функции Afactor, но создает структуру данных формы [u,[[f[1],e[1]],…,[f[n],e[n]]]] так, что p=u*f[1]^e[1]*…*f[n]^e[n], где каждый f[i] — неприводимый полином. Ниже даны примеры применения функции Afactor: > evala(AFactor(2*х^2+4*х-6));2(x+3)(х-1) > evala(AFactor(х^2+2*у^2));(х - RootOf(_Z² + 2)y) (x + RootOf(_Z² + 2)y) > expand((x-1) * (x-2) * (x-3) * (x-4));x4 - 10 x3 + 35 x2 - 50 x + 24 > AFactor(%);AFactor(x4 - 10 x3 + 35 x2 - 50 x + 24) > evala(%);(x-1)(x-2)(x-3)(x-4) > expand((x-1+I*2)*(x+1-I*2)*(x-3));x³ - 3x² + 3x - 9 + 4 I x-12 I > evala(AFactor(%));(x - 3)(x² + 3 + 4I) > evala(AFactors(х^2-2*у^2));[1, [[x - RootOf(_Z² - 2)y, 1], [x + RootOf(_Z² + 2)y, 1]]] Нетрудно заметить, что разложение полинома на множители позволяет оценить наличие у него корней. Однако для этого удобнее воспользоваться специальными функциями, рассмотренными ниже. 5.3.7. Вычисление корней полиномаДля вычисления действительных и комплексных корней полиномов служит уже известная нам функции solve(p, x), возвращающая список корней полинома p одной переменной. Кроме того, имеются следующие функции для вычисления корней полиномов: roots(р) roots(р, K) roots(р, х) roots(р, x, K) Эти функции вычисляют точные корни в рациональной или алгебраической области чисел. Корни возвращаются в виде [[r1,m1], [rn, mn]], где mi — это корень полинома, a mi — порядковый номер полинома. С действиями этих функций можно разобраться с помощью приведенных ниже примеров: > р:=х^4 1-9*х^3+31*х^2+59*х+60;р:=х4 + 9х3 + 31х2 + 59 х + 60 > solve(р,х);-3, -4, -1 + 2I, -1-2I > roots(р,х);[[-4, 1], [-3, 1]] > roots(х^2-4,х);[[2, 1], [-2, 1]] > expend((х-1)*(х-2)*(х-3)*(х-4));х4 -10х3 +35х2 - 50 х + 24 > roots(%,х);[[1, 1], [2, 1], [3, 1], [4, 1]] 5.3.8. Основные операции с полиномамиС полиномами могут выполняться различные операции. Прежде всего, отметим некоторые функции, которые относятся к одному полиному: psqrt(p) — возвращает квадрат полинома; proot(p,n) — возвращает n-ю степень полинома; realroot(p) — возвращает интервал, в котором находятся действительные корни полинома; randpoly(vars, eqns) — возвращает случайный полином по переменным vars (список) с максимальной степенью eqns; discrim(p, var) — вычисление дискриминанта полинома по переменной var; Primitive(a) mod p — проверка полинома на примитивность (возвращает true, если полином примитивен). Действие этих функций достаточно очевидно, поэтому ограничимся приведением примеров их использования (файл polop): > psqrt(х^2+2*х*у+у^2);у + x > proot(х^3+3*х^2+3*х+1, 3);x+1 > psqrt(x+y);_NOSQRT > proot(x+y, 2);_ NOROOT > р:=х^3-3*х^2+5*х-10;p:=x³ - 3x² + 5x - 10 > discrim(p,x);-1355 > readlib(realroot): > realroot(p);[[0, 4]] > randpoly([x],degree=10);63x10 + 57x8 - 59x5 + 45x4 - 8x3 - 93 > randpoly([x],degree=10);-5x9 + 99x8 - 61x6 - 50x5 - 12x3 - 18x > randpoly([x],degree=10);41x9 - 58x8 - 90x7 + 53x6 - x4 + 94x > Primitive(х^4+х+1) mod 2;true Обратите внимание на то, что для использования некоторых из приведенных функций необходим вызов их из стандартной библиотеки. Для функции randpoly приведенные результаты случайны, так что, скорее всего, их повторение невозможно. С полиномами можно выполнять обычные операции, используя для этого соответствующие операторы: > readlib(psqrt): > readlib(proot): > Primitive(х^4+х+1) mod 2;true > p1:=a1*x^3+b1*x^2+c1*x+d1: p2:=а2*х^2+b2*х+с2: > p1+p2;a1х³ + b1х² + c1x + d1 + a2x² + b2х + с2 > p1*p2;(a1x³ + b1x² + c1x + d1) + (a2x² + b2х + с2) > collect(%,х);a1a2x5 + (b1а2 + а1b2)х4 + (c1a2 + b1b2 + а1с2)х3 + (d1a2 + c1b2 + b1с2)х2 + (d1b2 + c1c2)x + d1c2 > p1/p2; 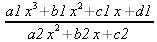 > expand(%,х); 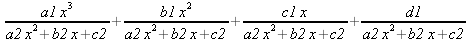 В целом надо отметить, что аппарат действий с полиномами в Maple хорошо развит и позволяет выполнять с ними практически любые математические операции. В частности, можно вычислять производные от полиномов и интегралы, у которых полиномы являются подынтегральными функциями: > diff(p1, х);3а1х² + 2b1х + c1 > diff(p1, x$2);6a1x + 2b1 > Int(p1,x)=int(p1,x); 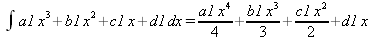 > Int(p1,х=0..1)=int(p1,х=0..1); 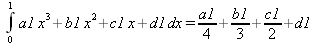 5.3.9. Операции над степенными многочленами с отрицательными степенямиХотя в подавляющем большинстве случаев используются степенные многочлены (полиномы) с положительными степенями, Maple не накладывает особых ограничений и на многочлены с отрицательными степенями. Например, можно задать такой степенной многочлен: > pp:=а*х^(-2)+b*x^(-1)+c*x+d+e*x^2+f*х^3; 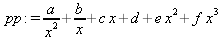 Нетрудно показать, что с ним можно выполнять различные операции: > рр+рр; 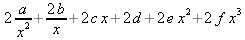 > рр-рр;0 > pp^2 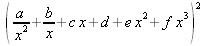 > simplify(%); 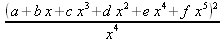 > Diff(pp, x)=diff(pp, x) 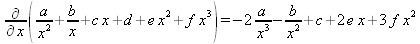 > Int(pp,x); 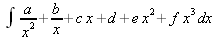 > int(рр,х); 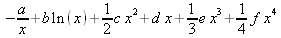 Хотя Maple и не накладывает ограничений на применение степенных многочленов (полиномов) с отрицательными степенями свойства таких полиномов заметно отличаются от свойств полиномов с положительными степенями, поэтому при применении первых надо проявлять известную осторожность. 5.4. Работа с ортогональными полиномами5.4.1. Состав пакета orthopolyОртогональные многочлены (полиномы) находят самое широкое применение в различных математических расчетах. В частности они широко используются в алгоритмах интерполяции, экстраполяции и аппроксимации различных функциональных зависимостей, где свойство ортогональности обеспечивает оценку погрешности приближения и сведение ее к минимуму — вплоть до нуля. В пакете orthopoly системы Maple 9.5 задано 6 функций: > with(orthopoly);[G, Н, L, Р, Т, U] Однобуквенные имена этих функций отождествляются с первой буквой в наименовании ортогональных полиномов. Вопреки принятым в Maple правилам, большие буквы в названиях этих полиномов не указывают на инертность данных функций — все они являются немедленно вычисляемыми. В данном разделе функции этого пакета будут полностью описаны. Отметим определения указанных функций: G(n,a,x) — полином Гегенбауэра (из семейства ультрасферических полиномов); H(n,x) — полином Эрмита; L(n,x) — полином Лагерра; L(n,a,x) — обобщенный полином Лагерра; P(n,x) — полином Лежандра; P(n,a,b,x) — полином Якоби; T(n,x) — обобщенный полином Чебышева первого рода; U(n,x) — обобщенный полином Чебышева второго рода. Свойства ортогональных многочленов хорошо известны. Все они характеризуются целочисленным порядком n, аргументом х и иногда дополнительными параметрами а и b. Существуют простые рекуррентные формулы, позволяющие найти полином n-го порядка по значению полинома (n-1)-го порядка. Эти формулы и используются для вычисления полиномов высшего порядка. 5.4.2. Вычисление ортогональных полиномовНиже представлены примеры вычисления ортогональных полиномов (файл orthpol): > G(0, 1, х);1 > G(1, 1, х);2х > G(1, 1, 5);10 > Н(3, х);8x³ - 12х > L(3, х); 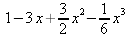 > L(2, а, х); 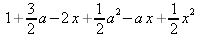 > Р(2, х); 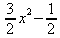 > Р(2, 1, 1, х); 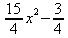 > Т(5, х);16х5 - 20х3 + 5х > U(5, х);32х5 - 32х3 + 6х В отличие от ряда элементарных функций, ортогональные многочлены определены только для действительного аргумента х. При комплексном аргументе ранее результат просто повторял исходное выражение с многочленом: > evalf(U(2,2+3*I));Р(2, 2+3I) Но уже в Maple 9 ортогональные полиномы с комплексными аргументами могут вычисляться: > evalf(U(2,2+3*I));-21. +48.I Ортогональные многочлены не определены и для дробного показателя n. Впрочем, надо отметить, что такие многочлены на практике используются крайне редко. 5.4.3. Построение графиков ортогональных полиномовПредставляет интерес построение графиков ортогональных многочленов. На рис. 5.6 построены графики ряда многочленов Гегенбауэра и Эрмита. На рис. 5.7 построены графики ортогональных многочленов Лагерра и Лежандра. Наконец на рис. 5.8 даны графики ортогональных многочленов Чебышева T(n, х) и U(n, x). 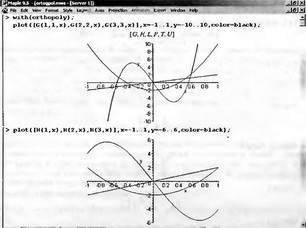 Рис. 5.6. Графики ортогональных многочленов Гегенбауэра и Эрмита 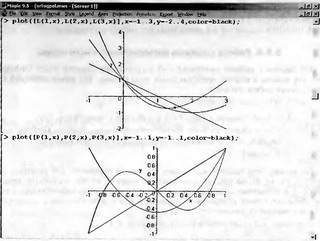 Рис. 5.7. Графики ортогональных многочленов Лагерра и Лежандра 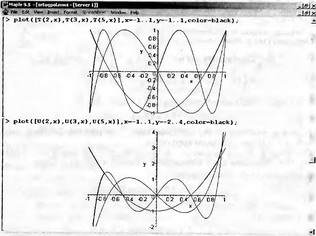 Рис. 5.8. Графики ортогональных многочленов Чебышева Приведенные графики дают начальное представление о поведении ортогональных многочленов. К примеру, многочлены Чебышева имеют минимальное отклонение от оси абсцисс в заданном интервале изменения х. Это их свойство объясняет полезное применение таких многочленов при решении задач аппроксимации функций, которые рассматриваются в этой главе далее. Можно порекомендовать читателю по их образцу и подобию построить графики ортогональных многочленов при других значения параметра n и диапазонах изменения аргумента х. 5.4.4. Работа с рядами ортогональных многочленовДля работы с рядами ортогональных многочленов имеется пакет OrthogonalSeries для работы с рядами ортогональных многочленов. Он имеет довольно представительный набор функций: > with(OrthogonalSeries);[Add, ApplyOperator, ChangeBasis, Coefficients, ConvertToSum, Copy, Create, Degree, Derivate, DerivativeRepresentation, Evaluate, GetInfo, Multiply, PolynomialMultiply, ScalarMultiply, SimplifyCoefficients, Truncate] Поскольку этот пакет представляет интерес, в основном, для опытных математиков, мы не будем рассматривать его функции (в целом достаточно простые) подробно и ограничимся несколькими примерами. В следующем примере с помощью функции Create создается бесконечный ряд с ортогональным многочленом Эрмита в составе базового выражения ряда: > OrthogonalSeries[Create](u(n),HermiteH(n,x));  В другом примере показано представление полиномиального выражения в новом базисе с ортогональными многочленами Чебышева с помощью функции ChangeBasis: > OrthogonalSeries[ChangeBasis](1+3*у*х^2+у^3*х, ChebyshevT(n,х), ChebyshevU(m, y));1 + ¾ChebyshevT(2, x) ChebyshevU(1, y) + ¾ChebyshevU(1, y) + ½ChebyshevT(1, x) ChebyshevU(1, y) > OrthogonalSeries[Evaluate](%);3x²y + yx + 1 Обратите внимание на то, что новое выражение после исполнения команды Evaluate приняло вид исходного выражения. Следующий пример демонстрирует создание ряда на основе ортогональных многочленов Чебышева и его копирование с помощью функции Сору: > S:=Create((-1)^n/n!, ChebyshevT(n, х)); 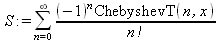 > Т:=Сору(S); 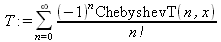 Вычисление производной от ряда с ортогональными многочленами представлено ниже: > S := Create(u(n),ChebyshevT(n,х));  > Derivate(S, х); 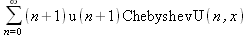 Еще один пример демонстрирует операцию скалярного умножения ряда с помощью функции ScalarMultiply: > S := Create(n+1,Kravchouk(n,p,q,x)); 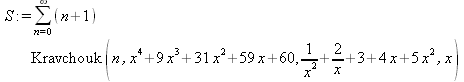 > ScalarMultiply(alpha, S); 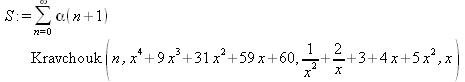 > simplify(%); 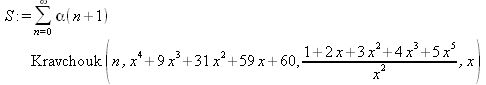 5.5. Пакет PolynomialTools5.5.1. Обзор возможностей пакета PolynomialToolsДля выполнения ряда специальных операций с полиномами или создания полиномов с заданными свойствами служит пакет PolynomialTools. Этот пакет имеет небольшое число функций: > with(PolynomialTools);[CoefficientList, CoefficientVector, Hurwitz, IsSelfReciprocal, MinimalPolynomial , PDEToPolynomial, PolynomialToPDE, Shorten, Shorter, Sort, Split, Splits, Translate] В пакет входят функции расщепления, сортировки и преобразования полиномов (в том числе в дифференциальные уравнения и наоборот) и др. 5.5.2. Функции для работы с полиномамиРассмотрим несколько функций пакета PolynomialTools общего характера. Функция IsSelfReciprocal(a, х, 'р') — проверяет полином а(х) на условие соeff(a,x,k)=coeff(a,x,d-k) для всех k=0..d, где d=degree(a, х) — порядок полинома. Если это условие выполняется, то возвращается логическое значение true, иначе — false. Если порядок d четный и если задан третий аргумент р, то р будет представлять полином P порядка d/2, такой, что x^(d/2)*P(x+1/x)=а. При нечетном d, полином а будет взаимо-обратным, что подразумевает деление на х+1. В этом случае если p указано, результат вычисляется в форме а/(х+1). Примеры применения этой функции представлены ниже (файл poltools): > with(PolynomialTools): IsSelfReciprocal(х^4+х^3+х+1, x, 'p');true > p;-2 + x + x² > IsSelfReciprocal(х^5-3*х^4+х^3+х^2-3*х+1, x, 'p');true > p;3-4x+x² > r := evalf(1+sqrt(2));r := 2.414213562 Функция MinimalPolynomial(r, n, acc) возвращает полином минимальной степени не превышающей n, имеющий корень r. Необязательный аргумент acc задает погрешность приближения. Функция MinimalPolynomial(r, n) использует решетчатый алгоритм и находит полином степени n (или менее) с наименьшими целыми коэффициентами. Корень r может быть действительным или комплексным. Результат зависит от значения переменной окружения Digits. По умолчанию acc задано как 10^(Digits-2). Примеры применения данной функции: > MinimalPolynomial(r, 2);-1 - 2_Х + _Х² > r := 1+sqrt(2);r:= 1 + √2 > ( r, 2 );1+√2, 2 > MinimalPolynomial( 1.234, 3 );-109 + 61_Х - 5_Х² + 22_ X³ > fsolve( %, X );1.234000001 Функция Split(a, х, b) служит для расщепления полинома а с независимой переменной х. Параметр b — не обязательный. Функция Split(a, х) осуществляет комплексную факторизацию инвариантного полинома а по х. Если третий аргумент b задан, он представляет множество элементов {t1, … ,tm}, таких что полином а расщепляется над K=Q(t1, …, tm), где Q означает поле рациональных чисел. Примеры: > Split(х^2+х+1,х);(х - RootOf(_Z² + _Z + 1))(х + 1 + RootOf(_Z² + _Z + 1)) > Split(х^2+у*х+1+у^2, x, 'b');(x - RootOf(_Z² + y_Z + 1 + r))(x + y + RootOf(_Z² + y_Z + 1 + y²)) > b;{RootOf(_Z² + у _Z + 1 + y²)} В пакете определена еще одна подобная функция Splits, с которой можно познакомиться по справке на нее. Функция Translate(a, х, х0) преобразует полином а(х) с подстановкой х=х+х0, где х0 — константа. Примеры применения этой функции даны ниже: > Translate(х^2, х, 1);1 + 2x + x² > expand(eval(х^2,х=х+1));1 + 2х + х² > Translate(х^3,х,2);8 + 12х + 6х² + х³ > expand(eval(х^3,х=х+2));8 + 12х + 6х² + х³ > Translate((х+1)^3,х,-1);x³ 5.5.3. Функции сортировки полиномовДля сортировки полиномов предназначены следующие три функции: Shorter(f, g, х) Sort(v, х) Shorten(f, x) Здесь f и g полиномы, v — список полиномов и x — независимая переменная. Функции отличаются характером сортировки. Функция Shorter определяет полином f как более короткий, чем g, по следующим признакам: меньшая длина, меньшее имя независимой переменной х, не дробный и меньшая степень других переменных. Функция Sort сортирует лист полиномов х по признакам, определяемым Shorter. Функция Shorten использует преобразования Мёбиуса. Многочисленные детали ее применения можно найти в справке по данной функции. Примеры применения функций сортировки: > Shorten(х^2+х+1,х);x² + 3 > Shorten(3*х^3+18*х+14,х);x³ - 6 > Shorten(х^4+32);х4 + 2 > Shorter(х^3,х+5,х);false > Sort([х^3,х^2,х+1,х+5]); Error, (in sort_poly) sort_poly uses a 2nd argument, x, which is missing > Sort([х^3,х^2,x+1,x+5],x);[1 + x, x + 5, x², x³] 5.5.4. Функции преобразования полиномов в PDE и обратноФункция PolynomialToPDE(polys, vars, depvars) преобразует полиномы polys по независимым переменным vars в дифференциальные уравнения с частными производными (PDE). Другая функция PDEToPolynomial(pdes, vars, depvars) осуществляет обратное преобразование. Следующие примеры иллюстрируют применение этих функций: > S:= PolynomialToPDE([(х^2 - 2*х + 1)*u + x^3*v], [х], [u,v]); 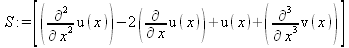 > PDEToPolynomial(S, [х], [u,v]);[(x² - 2x + 1)u + x³v] 5.6. Введение в интерполяцию и аппроксимацию5.6.1. Основные понятияЕсли некоторая зависимость y(х) представлена рядом табличных отсчетов yi(хi), то интерполяцией принято называть вычисление значений y(х) при заданном х, расположенном в интервале между отсчетами. За пределами общего интервала определения функции [a, b], то есть при x<a и x>b вычисление y(x) называют экстраполяцией (или, иногда, предсказанием значений функции). В данном случае речь идет об одномерной интерполяции, но возможны двумерная интерполяция функций двух переменных z(х, у) и даже многомерная интерполяция для функций многих переменных. Интерполяция и экстраполяция часто выполняются по некоторой скрытой, но подразумеваемой, зависимости. Например, если узловые точки функции соединить отрезками прямых, то будем иметь многоинтервальную линейную интерполяцию данных. Если использовать отрезки параболы, то интерполяция будет параболической. Особое значение имеет многоинтервальная сплайн-интерполяция, области применения которой уже сейчас весьма обширны и непрерывно расширяются. Интерполяция рядом Фурье (набором синусоидальных функций) также достаточно хорошо известна, она эффективна при интерполяции периодических функций. Аппроксимацией в системах компьютерной математики обычно называют получение приближенных значений какого-либо выражения. Однако под аппроксимацией функциональных зависимостей подразумевается получение некоторой конкретной функции, вычисленные значения которой с некоторой точностью аналогичны аппроксимируемой зависимости. Обычно предпочитают найти одну зависимость, приближающую заданный ряд узловых точек. Часто для этого используют степенные многочлены — полиномы. Здесь мы будем рассматривать такие виды аппроксимации, которые дают точные значения функции y(x) в узловых точках в пределах погрешности вычислений по умолчанию. Если аппроксимирующая зависимость выбирается из условия наименьшей среднеквадратической погрешности в узловых точках (метод наименьших квадратов), то мы имеем регрессию или приближение функций по методу наименьших квадратов. 5.6.2. Полиномиальная аппроксимация и интерполяция аналитических зависимостейРассмотрим основы полиномиальной аппроксимации (приближения) функциональных зависимостей. Пусть приближаемая функция φ(х) должна совпадать с исходной функцией f(х) в (n+1)-точке, то есть должно выполняться равенство: φ(хi)=f(хi)=fi, i = 0, …, n. В качестве приближающей функции примем алгебраический полином: Выбор конкретного значения n во многом определяется свойствами приближающей функции, требуемой точностью, а также выбором узлов интерполяции. В случае аналитической функциональной зависимости выбор степени полинома может быть любым и чаще всего определяется компромиссом между сложностью полинома, скоростью его вычисления и погрешностью. В качестве критерия согласия принимается условия совпадения функций f и q в узловых точках: f(хi) = Рn(хi), (i=0, 1, … n). (5.2)Полином Рn(х) удовлетворяющий данному условию будет интерполяционным полиномом. Для задачи интерполирования в интервале [a, b] выбираются значения аргументов а≤х0<x1<…<хn≤b, которые соответствуют значениям fi=f(хi) (i=0, 1, ..., n) функции f. Для этой функции будет существовать и притом единственный полином степени не выше n, который принимает в узлах х, заданные значения fi. Для нахождения этого полинома решается система алгебраических уравнений а0хtn +a1 хtn-1 + ... +аn = fi, (i=0, 1, ..., n).Подставив полученные значения a_k в равенство (5.1) можно получить обобщенную форму представления интерполяционного полинома Получив интерполяционный полином (5.3), необходимо выяснить, насколько близко он приближается к исходной функции в других точках отрезка [a, b]. Обычно для этого строится график f(x) и Рn(х) и график их разности, т. е. абсолютной погрешности. Последняя определяется выражением: Вопреки существующему мнению о быстрой потери точности полиномиальной аппроксимации при n>(5–7) погрешность ее быстро уменьшается при увеличении n. Но это только при условии, что все вычисления выполняются точно! При выборе метода приближения необходимо обеспечить по возможности более высокую точность приближения и одновременно простоту построения φ(х) по имеющейся информации о приближаемой функции f(х). 5.6.3. Интерполяционный метод Лагранжа.При решении практических задач часто используют специальные виды интерполяционных полиномов, которые упрощают некоторые вычислительные процедуры. Данный метод предполагает введение вспомогательного полинома li(х) степени n. Полином li(х) в точке х, должен быть равен 1, а в остальных точках отрезка интерполяции должен обращаться в нуль. Удовлетворяющий этому полином может быть представлен в виде: Это выражение известно как интерполяционный полином Лагранжа. Важным достоинством ее является то, что число арифметических операций, необходимых для построения полинома Лагранжа, пропорционально n² и является наименьшим для всех форм записи. Данная форма интерполяционного полинома применима как для равноотстоящих, так и для неравноотстоящих узлов. Достоинством является и то, что интерполяционный полином Лагранжа удобен, когда значения функций меняется, а узлы интерполяции неизменны, что имеет место во многих экспериментальных исследованиях. Рекомендуется использовать запись интерполяционного полинома в форме Лагранжа при теоретических исследованиях при изучении вопроса сходимости Ln(f, х) к f при n→∞. К недостаткам этой формы записи можно отнести то, что с изменением числа узлов необходимо все вычисления проводить заново. Выражение (5.4) можно записать в более компактной форме: Теоретически максимальную точность обеспечивает полином высокой степени. Однако на практике часто используется полином невысокой степени (линейная и квадратичная интерполяция) с увеличением степени интерполяционного полинома возрастают колебательные свойства полинома. Аппроксимация с помощью интерполяционного полинома Лагранжа является достаточно эффективной, когда интерполируются гладкие функции и число n является малым. В частности в математическом обеспечении компьютерных средств имеется стандартные подпрограммы аппроксимации, в которых реализована формула Лагранжа. 5.6.4. Интерполяционный метод НьютонаНа практике для повышения точности интерполяционного полинома незначительно увеличивают количество узлов интерполяции. В этом случае использование метода Лагранжа неудобно, так как добавление дополнительных узлов приводит необходимости пересчета всего интерполяционного полинома в целом. Эти недостатки устраняются, если записать полином Лагранжа, используя интерполяционный метод Ньютона. Используя понятия разделенных разностей для полинома Ньютона можно получить выражение: Nn(x) = f(x0) + (x-x0)f(x1, x0) + (x-x0)(x-x1)f(x0, x1, x2) + … + (x-x0)(x-x1)…(x-xn)f(x, x0, x1, …, xn) (5.6)Представление интерполяционного полинома в форме Ньютона является более удобным в практических расчетах. На практике часто заранее неизвестно количество узлов и, следовательно, степень интерполяционного полинома. Для повышения точности интерполяции в сумму могут быть добавлены новые члены, что требует подключение новых узлов. Добавление новых узлов интерполяции приводит лишь к появлению новых слагаемых полинома, без изменения уже существующих, что не требует пересчета всех коэффициентов заново. При добавлении новых узлов интерполяции неважно, в каком порядке они подключаются, но существует одно условие — узлы х, не должны совпадать. 5.6.5. Итерационно-интерполяционный метод ЭйткенаИтерационно-интерполяционный метод Эйткена позволяет свести вычисления коэффициентов интерполяционного полинома Лагранжа, с учетом его равенства в узлах интерполяции с исходными данными к вычислению функциональных определителей второго порядка. При этом эффективность метода повышается в тех случаях, когда нет необходимости в получении приближенного аналитического выражения функции f(х), заданной таблично, а требуется лишь определить значение в некоторой точке х*, отличной от узловых точек. Этот метод заключается в последовательной линейной интерполяции. Процесс вычисления f(x*) состоит в следующем: необходимо пронумеровать узлы интерполяции, например, в порядке убывания их от х*. Затем для каждой узловой точки интерполяции строятся соотношения: 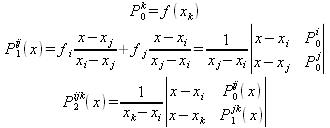 которые является интерполяционными полиномами, построенными соответственно по узлам хi, хj, хk. Продолжая этот процесс, имеем следующий полином: Полученный полином является интерполяционным полиномом, построенный по узлам хi, xj, …, хk, хm. Это утверждение верное, так как Рn-1ij…k(х) и Рn-1j…km(x) являются интерполяционными полиномами. При его реализации предполагается, что функция гладкая, а также критерием оценки погрешности определяется некоторое значение, определяемое условиями конкретной задачи. 5.6.6. Чебышевская интерполяцияМетод Чебышева был создан для оптимального выбора узлов интерполяции, если это возможно при решении конкретной задачи, и для получения минимально возможной погрешности аппроксимации. Предполагается, что в выборе расположения узлов интерполяции ограничений нет, и предполагается, что узлы выбираются произвольно. Ставится задача о наилучшем выборе узлов. Наилучшими узлами х, следует признать те, для которых выражение max[a,b]|ωn(x)| минимально для рассматриваемого класса функций (алгебраических полиномов). Определение этих узлов сводится к нахождению корней полинома, наименее уклоняющихся от нуля на [a, b]. Такой полином порождается полиномом Чебышева первого рода Tn+1. Полиномы Чебышева определены в интервале [-1,1]. Для перевода интерполяции в интервале [a, b], выполняется линейная замена переменной х: 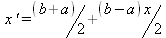 В качестве узлов интерполяции берутся корни полинома Чебышева: Тогда погрешность Чебышевской интерполяции определяется выражением: 5.6.7. Сплайновая интерполяция, экстраполяция и аппроксимацияИспользование одной интерполяционной формулы для большого числа узлов нецелесообразно, так как при этом интерполяционный полином сильно проявляет свои колебательные свойства, и значение между узлами могут сильно отличаться от значений интерполируемой функции. Одна из возможностей преодоления этого недостатка заключается в применении сплайн-интерполяции. Наиболее известным и широко применяемым является случай сплайновой интерполяции, когда между двумя точками строится полином n-й степени который в узлах интерполяции принимает значения интерполируемой функции и непрерывен вместе со своими (n-1)-ми производными. Такой кусочно-непрерывный интерполяционный полином называется сплайном. Его коэффициенты находят из условий в узлах интерполяции — равенства значений сплайна и приближаемой функции, а также равенства (n-1)-й производной соответствующих полиномов. Максимальная по всем частичным отрезкам степень полинома является степенью сплайна. Одним из наиболее распространенных интерполяционных сплайнов является кубический интерполяционный сплайн. Для вывода уравнения кубического интерполяционного сплайна можно воспользоваться его представлением в виде гибкой линейки, изогнутой таким образом, что она проходит через значения функции в узлах, то есть, является упругой рейкой в состоянии равновесия. Это его состояние описывается уравнением S'''(х)=0, где S'''(х) — четвертая производная. Из этого следует, что между каждой парой соседних узлов интерполяционная формула записывается в виде полинома третьей степени. Этот полином удобно представить следующим образом: S(x) = аi + bi(x-xi-1) + с(х-хi-1)² + di(x–хi-1)³, xi-1≤х≤xi, i = 1, 2, ..., n.Система Maple позволяет легко вычислять коэффициенты кубических полиномов. Метод сплайновой интерполяции дает хорошие результаты при интерполяции непрерывных функций с гладкими производными 1-ой и 2-ой степени. При этом кубическая сплайновая интерполяция, построенная по узлам fi=f(хi), i=0,1,…,n, будет иметь минимум кривизны по сравнению с любой интерполяционной функцией, имеющей непрерывные первую и вторую производные. Выполнение сплайн-интерполяции функций с резким изменением производных дает, как правило, большие ошибки. Сплайны более высоких порядков, чем третий, используется редко, так как при вычислении большого числа коэффициентов может накапливаться ошибка, приводящая к значительным погрешностям. По сравнению с другими математическими конструкциями сплайны обладают следующими преимуществами: они обладают лучшими аппроксимирующими свойствами, что при равных информационных затратах дает большую точность или равную точность при менее информационных исходных данных. Для увеличения точности часто уменьшают величину шага интерполяции, что увеличивает число узлов. В случае интерполяционных полиномов это связано с возрастанием их степени, что имеет недостатки. Степень же сплайна не изменяется при увеличении количество узлов интерполяции. Это принципиальный момент теории сплайнов. 5.6.8. Рациональная интерполяция и аппроксимацияБольшую точность приближения по сравнению полиномиальным приближением можно получить, если исходную функцию заменить, используя рациональную интерполяцию при которой аппроксимирующая функция ищется как отношение двух полиномов. Наиболее важным свойством рациональных функций является то, что ими можно приближать такие функции, которые принимают бесконечные значения для конечных значений аргумента и даже внутри интервала его изменения. Итак, при задании f(х1), …, f(хn) приближение к f(x) ищется в виде Коэффициенты аi, bi находятся из совокупности соотношений R(хj)=f(xj) (j=1,…,n), которые можно записать в виде 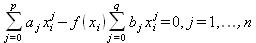 Данное уравнение образует систему n линейных уравнений относительно n+1 неизвестных. Такая система всегда имеет нетривиальное решение. Функция R(x) может быть записана в явном виде в случае n нечетное, если р=q, и n четное, если р-q=1. Для записи функции R(x) в явном виде следует вычислять так называемые обратные разделенные разности, определяемые условиями 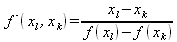 и рекуррентным соотношением 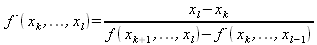 Интерполирование функций рациональными выражениями обычно рассматривают на основе аппарата цепных дробей. Тогда интерполирующая рациональная функция записывается в виде цепной дроби 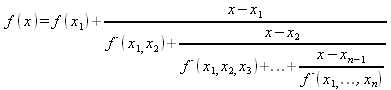 Использование рациональной интерполяции часто целесообразнее интерполяции полиномами в случае функций с резкими изменениями характера поведения или особенностями производных в точках. 5.6.9. Метод наименьших квадратов (МНК)При обработке экспериментальных данных, полученных с некоторой погрешностью, интерполяция становиться неразумной. В этом случае целесообразно строить приближающую функцию таким образом, чтобы сгладить влияние погрешности измерения и числа точек эксперимента. Такое сглаживание реализуется при построении приближающей функции по методу наименьших квадратов. Рассмотрим совокупность значений таблично заданной функции fi в узлах хi при i=0,1,…,n. Предположим, что приближающаяся функция F(x) в точках х1, х2, …, хn имеет значения 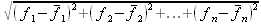 была наименьшей, что соответствует следующему: то есть сумма квадратов должна быть наименьшей. Задачу приближения функции f(х) теперь можно формулировать иначе. Для функция f(х), заданной таблично, необходимо найти функцию F(x) определенного вида так, чтобы сумма квадратов (5.12) была наименьшей. Выбор класса приближающихся функций определяется характером поведения точечного графика функции f. Это могут быть линейная зависимость, любые элементарные функции и т.д. Практически вид приближающей функции F можно определить, построив точечный график функции f(х), а затем построить плавную кривую, по возможности наилучшим образом отражающую характер расположения точек. По полученной кривой выбирают вид приближающей функции. Когда вид приближающей функции выбран, то последующая задача сводится к отысканию значений параметров функции. Рассмотрим метод нахождения параметров приближающей функции в общем виде на примере приближающей функции с тремя параметрами f=F(x, с, b, с). Тогда имеем Сумма квадратов разностей соответствующих значений функций f и F будет иметь вид: Сумма (5.14) является функцией φ(a, b, с) трех переменных a, b, с. Задача сводится к отысканию ее минимума. Для этого используем необходимое условие экстремума: 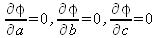 или Решив эту систему (5.15) трех уравнений с тремя неизвестными относительно параметров a, b, с, получим конкретный вид искомой функции F(x, a, b, с). Изменение количества параметров не приведет к изменению сущности метода, а отразится только на количестве уравнений в системе (5.15). Как следует из начальных условий, найденные значения функции F(x, а, b, с) в точках x1, х2, …, хn будут отличаться от табличных значений y1, у2, …, уn. Значение разностей fi-F(xi, a, b, c,) = εi, i=1, 2, …, nбудет определять отклонение измеренных значений f от вычисленных по формуле (5.14). Для найденной эмпирической формулы (5.14) в соответствии с исходными табличными данными можно найти сумму квадратов отклонений Она, в соответствии с принципом наименьших квадратов для заданного вида приближающей функции и ее найденных параметров (параметры a, b, с), должна быть наименьшей. Из двух разных приближений одной и той же табличной функции, следуя принципу наименьших квадратов, лучшим нужно считать тот, для которого сумма (5.16) имеет меньшее значение. 5.6.10. Тригонометрическая интерполяция рядами ФурьеПри тригонометрической интерполяции используются тригонометрические полиномы — линейные комбинации тригонометрических функций sin(nx) и cos(nx). Этот вид интерполирования применяется для процессов, которые отражают циклические процессы, связанные с периодическими функциями [52–54]. Известно, что такие функции удобно представлять в виде тригонометрического ряда или его частичной суммы с достаточной степенью точности. Функциональный ряд вида называется тригонометрическим. Его коэффициенты аn и bn — действительные числа, не зависящие от х. Если этот ряд сходится для любого х из промежутка [-π, π], тогда он определяет периодическую функцию f(x) с периодом Т=2π. Ряд вида (5.17) называется рядом Фурье для интегрируемой на отрезке [-π, π] функции f(х), если коэффициенты его вычисляются по следующим правилам: В практических расчетах, как правило, ограничиваются конечным числом первых членов ряда Фурье. В результате получается приближенное аналитическое выражение для функции f(х) в виде тригонометрического полинома N-го порядка 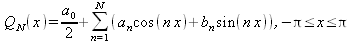 Но соотношения для вычисления коэффициентов Фурье (5.18)–(5.20) пригодны для случая аналитического задания исходной функции. Если функция задана в виде таблицы, то возникает задача приближенного отыскания коэффициентов Фурье по конечному числу имеющихся значений функции. Таким образом, формулируется следующая задача практического, гармонического анализа: аппроксимировать на интервале (0, T) тригонометрический полином N-го порядка функцию у=f(х), для которой известны m ее значений уk=f(хk) при хk=kТ/m, где k=0, 1, 2, …, m-1. Тригонометрический полином для функции, определенной на интервале (0, Т), имеет вид: Коэффициенты аn и bn определяются следующими соотношениями: Применяя в соотношениях (5.22)–(5.23) формулу прямоугольников для вычисления интегралов по значениям подынтегральных выражений в точках хk=kT/m, где k=0, 1, 2, …, m-1, имеем Таким образом, тригонометрический полином (5.21), коэффициенты аn и bn находятся по формулам (5.24)–(5.25), служит решением поставленной задачи. При этом, коэффициенты (2.44)–(2.45) минимизируют сумму квадратов отклонений 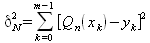 В случае, когда m=2N коэффициенты аn и bn для n=0, 1, 2, …, N определяется соотношениями (5.24)–(5.25), а коэффициент aN определяется соотношением: 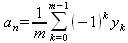 Сам же полином QN(x) становится интерполяционным полиномом, так как в этом случае при любом bN выполняется соотношения QN(xk)=yk для всех хk=kТ/m, где k = 0, 1, 2, …, m-1. 5.7. Аппроксимация зависимостей в Maple5.7.1. Аппроксимация аналитически заданных функцийВ Maple 9.5 если функция задана аналитически, то наиболее простым способом нахождения ее аппроксимирующей зависимости является применение функции convert, которая позволяет представить функцию в виде иного выражения, чем исходное. Например, при опции polynom осуществляется полиномиальная аппроксимация. Это поясняют следующие примеры (файл aprox): > convert(taylor(exp(х),х,5),polynom); 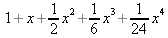 > f:=х->(х^3+х)/(х^2-1); 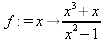 > convert(f(x),parfrac, x); 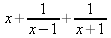 На рис. 5.9 представлен пример полиномиальной аппроксимации хорошо известной статистической функции erfc(x). Для полинома задана максимальная степень 12, но ввиду отсутствия в разложении четных степеней максимальная степень результата оказывается равна 11. 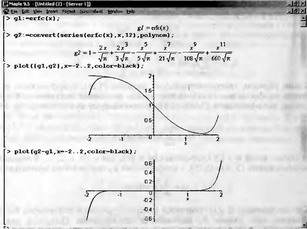 Рис. 5.9. Пример полиномиальной аппроксимации функции erfc(x) — сверху построены графики исходной функции и полинома, снизу график абсолютной погрешности Как видно из приведенного рисунка, в интервале изменения x от -1,4 до 1,4 аппроксимирующее выражение почти повторяет исходную зависимость. Однако затем график аппроксимирующей функции быстро отходит от графика исходной зависимости и погрешность аппроксимации резко возрастает. При этом он ведет себя иначе даже качественно, никоим образом не показывая асимптотическое поведение, характерное для исходной зависимости. Это говорит о том, что полиномиальная аппроксимация плохо подходит для экстраполяции (предсказания) зависимостей. Как уже отмечалось, считается, что полиномиальная аппроксимация дает большую погрешность при степени полинома более 5–6. Однако, этот вывод базируется на том, что большинство вычислительных программ работает всего с 5–10 точными знаками в промежуточных и окончательных результатах. Maple по умолчанию имеет 10 точных знаков чисел. Это показывает следующий пример: > restart:Digits;10 Таким образом, Maple, как и любая другая программа может давать большую погрешность при высоких степенях аппроксимирующего полинома. В этом убеждает рис. 5.10, на котором представлена программа полиномиальной аппроксимации функции синуса с возможностью выбора степени полинома N. Программа автоматически задает N+1 отсчетов функции синуса и затем выполняет ее полиномиальную аппроксимацию для N=10 и Digits=8. Результат аппроксимации совершенно неудовлетворительный — видно, что программа под конец пошла вразнос — так именуются хаотические изменения кривой аппроксимирующей функции. 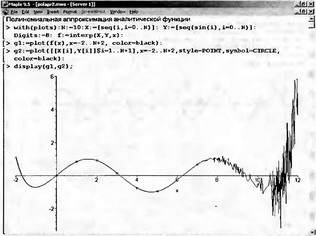 Рис. 5.10. Пример неудачной аппроксимации синуса при N=10 и Digits=8 Практическая рекомендация при полиномиальной аппроксимации выглядит следующим образом — число точных цифр в промежуточных результатах Digits должно на несколько цифр превышать значение N. Рисунок 5.11, приведенный для N=10 и Digits=15 удовлетворяет этому правилу. При этом все точки точно укладываются на кривую полинома 10-го порядка. Однако за пределами интервала, в котором находятся узловые точки, кривая аппроксимации резко отклоняется от функции синуса. Это говорит о том, что достаточно точная экстраполяция (предсказание) при полиномиальном приближении невозможна — повышение степени полинома лишь ухудшают возможности экстраполяции. 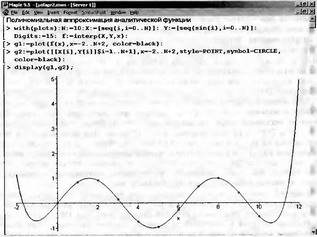 Рис. 5.11 Пример достаточно корректной аппроксимации синуса при N=10 и digits=15 Maple 9.5 является системой, позволяющей выполнять арифметические вычисления с практически произвольным числом точных цифр. Ограничения на это число накладывается объемом памяти ПК (для современных ПК не актуально) и возрастанием времени вычислений. В качестве примера аппроксимации полиномом высокой степени на рис. 5.12 приведен документ, осуществляющий аппроксимацию функции синуса для степени полинома N=30 при числе точных цифр Digits=40. Нетрудно заметить, что все 31 узловые точки прекрасно укладываются на кривую полинома и что за пределами расположения этих точек она резко отклоняется от синусоидальной функции. 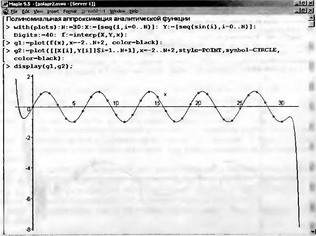 Рис. 5.12. Пример аппроксимации функции синуса полиномом степени N=30 при Digits=40 В целом аппроксимация полиномами высокой степени хотя и возможна, но непрактична, поскольку такие полиномами едва ли можно назвать простыми аппроксимирующими функциями. 5.7.2. Сплайн-интерполяция в MapleДля сплайн-интерполяции используется Maple-функция spline(X,Y,var,d). Здесь X и Y — одномерные векторы одинакового размера, несущие значения координат узловых точек исходной функции (причем в произвольном порядке), var — имя переменной, относительно которой вычисляется сплайн-функция, наконец, необязательный параметр d задает вид сплайна. Он может иметь цифровые 1, 2,3 или 4, либо символьные значения: linear — линейная функция, или полином первого порядка, quadratic — квадратичная функция, или полином второго порядка, cubic — полином третьего порядка, quartic — полином четвертого порядка. Если параметр d опущен, то сплайн-функция будет строиться на основе полиномов третьего порядка (кубические сплайны). Важно отметить, что за пределами узловых точек сплайны обеспечивают экстраполяцию, представляя данные в соответствии с первым полином слева и последним справа. Технику сплайновой аппроксимации наглядно поясняет рис. 5.13. На нем представлено задание векторов узловых точек X и Y и четырех сплайновых функций, по которым построены их графики. Для одной из функций (кубических сплайнов) показан вид сплайновой функции. 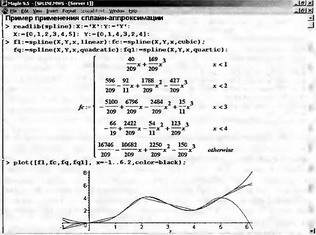 Рис. 5.13. Задание сплайновой аппроксимации и построение графиков полученных функций Как видно из рис. 5.13, сплайновая функция представляет собой кусочную функцию, определяемую на каждом отдельно. При этом на каждом участке такая функция описывается отдельным полиномом соответствующей степени. Функция plot «понимает» такие функции и позволяет без преобразования типов данных строить их графики. Для работы с кусочными функциями можно использовать функции convert и piecewise. Обычно удобно представлять на одном графике узловые точки и кривые интерполяции и экстраполяции. На рис. 5.14 дан пример такого рода. Здесь для одних и тех же данных, представленных векторами datax и datay заданы все 4 возможные типа сплайновой интерполяции/экстраполяции (заданы числами, указывающими на степень полиномов сплайн-функций). 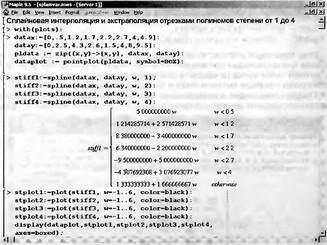 Рис. 5.14. Сплайновая интерполяция/экстраполяция при степени полиномов от 1 до 4 Вывод указан для степени полиномов 1, что соответствует линейной интерполяции/экстраполяции. Для других случаев вывод заблокирован двоеточием, поскольку выглядит очень громоздким. Тем не менее, читатель может просмотреть его, заменив двоеточие на точку с запятой. С помощью графической функции display выводятся как все кривые сплайновой интерполяции/экстраполяции, так и узловые точки — рис. 5.15. Полезно обратить внимание на плохую пригодность для экстраполяции сплайнов второго порядка. 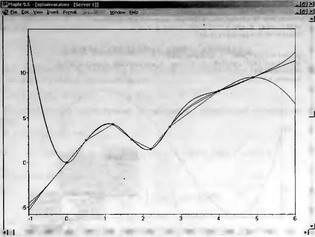 Рис. 5.15. Графики, построенные документом, представленным на рис. 5.14 Мы вернемся к рассмотрению сплайновой аппроксимации в конце этой главы при описании пакета расширения CurveFitting. 5.7.3. Полиномиальная интерполяция табличных данныхНа самом деле выполнять все расчеты для полиномиальной аппроксимации в Maple 9.5 не нужно, поскольку системы имеет реализующую данный алгоритм встроенную функцию interp(X,Y,v) или, в инертной форме, Interp(X,Y, v). Переменная v указывает имя переменной интерполяционного полинома. Векторы X и Y должны содержать n+1=N координат точек исходной зависимости, где n — степень интерполирующего полинома. Рисунок 5.16 показывает технику применения полиномиальной аппроксимации на основе функции interp с построением графика исходных точек и аппроксимирующего полинома. Нетрудно заметить, что график полинома проходит точно через исходные точки — они показаны квадратиками. 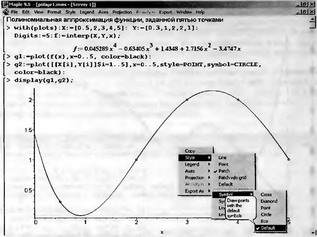 Рис. 5.16 Пример осуществления полиномиальной аппроксимации для таблично заданных данных (точек) В этом примере полезно присмотреться к визуализации результатов вычислений и совместному построению графика интерполирующего полинома и исходных точек. В частности, для построения последних использована обычная функция plot, позволяющая выводить на график точки с заданными координатами, причем не только в виде окружностей, но и в виде точек, маленьких крестиков, кружков, квадратов и других фигур. Для выбора типа точек и других параметров графика его надо выделить (установив указатель мыши в поле графика и щелкнув левой кнопкой) и нажать правую кнопку мыши — появится контекстно-зависимое меню с операциями форматирования графика. Приведем еще несколько примеров использования функции Interp: > Interp([2,5,6], [9,8,3], х) mod 11;8х² + 6х + 9 > alias(alpha=RootOf(х^4+х+1));α > a := Interp([0,1,alpha],[alpha,alpha^2,alpha^3], x) mod 2;a := x² + (α² + α + 1)x + α 5.8. Применение числовой аппроксимации функций5.8.1. Состав пакета numapproxДля более глубоких и продвинутых операций аппроксимации служит специальный пакет расширения numapprox. Этот пакет содержит небольшое число безусловно очень важных функций: > with(numapprox);[chebdeg, chebmult, chebpade, chebsort, chebyshev, confracform, hermite_pade, hornerform, infnorm, laurent, minimax, pade, remez] В их числе функции интерполяции и аппроксимации полиномами Чебышева, рядом Тейлора, отношением полиномов (аппроксимация Паде) и др. Все они широко применяются не только в фундаментальной математике, но и при решении многих прикладных задач. Рассмотрим их, начиная с функций аппроксимации аналитических зависимостей. 5.8.2. Разложение функции в ряд ЛоранаДля разложения функции f в ряд Лорана с порядком n в окрестности точки x=а (или x=0) служит функция laurent: laurent(f, х=а, n) laurent(f, x, n) Представленный ниже пример иллюстрирует реализацию разложения в ряд Лорана: > laurent(f(х),х=0,4);f(0) + D(f)(0)x + ½(D(2)(f)(0)x2 + ⅙(D(3)(f)(0)x3 + O(х4) > laurent(exp(х),х,5); 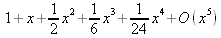 5.8.3. Паде-аппроксимация аналитических функцийДля аппроксимации аналитических функций одной из лучших является Паде-аппроксимация, при которой заданная функция приближается отношением двух полиномов. Эта аппроксимация способна приблизить даже точки разрыва исходной функции с устремлениями ее значений в бесконечность (при нулях полинома знаменателя. Для осуществления такой аппроксимации используется функция pade: pade(f, х=а, [m,n]) pade(f, х, [m,n]) Здесь f — аналитическое выражение или функция, x — переменная, относительно которой записывается аппроксимирующая функция, a — координата точки, относительно которой выполняется аппроксимация, m, n — максимальные степени полиномов числителя и знаменателя. Технику аппроксимации Паде непрерывной функции поясняет рис. 5.17. 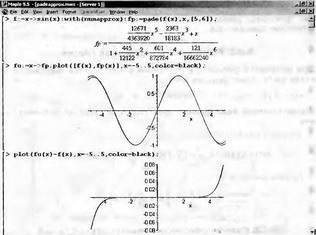 Рис. 5.17. Аппроксимация Паде для синусоидальной функции На рис. 5.17 представлена аппроксимация синусоидальной функции, а также построены графики этой функции и аппроксимирующей функции. Под ними дан также график абсолютной погрешности для этого вида аппроксимации. Нетрудно заметить, что уже в интервале [-π, π] погрешность резко возрастает на концах интервала аппроксимации. Важным достоинством Паде-аппроксимации является возможность довольно точного приближения разрывных функций. Это связано с тем, что нули знаменателя у аппроксимирующего выражения способны приближать разрывы функций, если на заданном интервале аппроксимации число разрывов конечно. На рис. 5.18 представлен пример Паде-аппроксимации функции tan(x) в интервале от -4,5 до 4,5, включающем два разрыва функции. 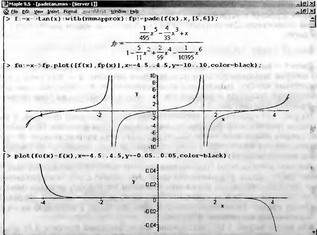 Рис. 5.18. Аппроксимация Паде для разрывной функции тангенса Как видно из рис. 5.18, расхождение между функцией тангенса и ее аппроксимирующей функцией едва заметны лишь на краях интервала аппроксимации. Оба разрыва прекрасно приближаются аппроксимирующей функцией и никакого выброса погрешности в точках разрыва нет. Такой характер аппроксимации подтверждается и графиком погрешности, которая лишь на концах интервала аппроксимации [-4.0, 4.0] достигает значений 0,01 (около 1%). 5.8.4. Паде-аппроксимация с полиномами ЧебышеваДля многих аналитических зависимостей хорошие результаты дает аппроксимация полиномами Чебышева. При ней более оптимальным является выбор узлов аппроксимации, что ведет к уменьшению погрешности аппроксимации. В общем случае применяется Паде-аппроксимация, характерная представлением аппроксимирующей функции в виде отношения полиномов Чебышева. Она реализуется функциями chebpade: chebpade(f, x=a..b, [m,n]) chebpade(f, x, [m,n]) chebpade(f, a..b, [m,n]) Здесь a..b задает отрезок аппроксимации, m и n — максимальные степени числителя и знаменателя полиномов Чебышева. Приведенный ниже пример показывает аппроксимацию Паде полиномами Чебышева для функции f=cos(x): > Digits:=10:chebpade(cos(x),x=0..1,5);0.8235847380 T(0, 2x-1) - 0.2322993716 T(1, 2 x-1) - 0.05371511462 T(2, 2x-1) + 0.002458235267 T(3, 2 х-1) + 0.0002821190574 T(4, 2x-1) - 0.7722229156-5 T(5, 2x-1) > chebpade(cos(x),x=0..1,[2,3]);(0.8162435876 T(0, 2x-1) - 0.1852356296 T(1, 2x-1) - 0.05170917481 T(2, 2x-1))/(T(0, 2x-1) + 0.06067214549 T(1, 2x-1) + 0.01097466398 T(2, 2x-1) + 0.0005311640964 T(3, 2 x-1)) 5.8.5. Наилучшая минимаксная аппроксимацияМинимаксная аппроксимация отличается от Паде-аппроксимации минимизацией максимальной абсолютной погрешности во всем интервале аппроксимации. Она использует алгоритм Ремеза (см. ниже) и реализуется следующей функцией: minimax(f, x=a..b, [m,n], w, 'maxerror') minimax(f, a..b, [m,n], w, 'maxerror') Здесь, помимо уже отмеченных параметров, w — процедура или выражение, maxerror — переменная, которой приписывается значение minimax-нормы. Ниже дан пример аппроксимации функции cos(x) в интервале [-3, 3]: > minimax(cos(х),х=-3..3,[2,3],1,'minmax'); 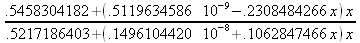 > minimax;.04621605601 5.8.6. Наилучшая минимаксная аппроксимация по алгоритму РемезаДля получения наилучшей полиномиальной аппроксимации используется алгоритм Ремеза, который реализует следующая функция: remez(w, f, a, b, m, n, crit, 'maxerror') Здесь w — процедура, представляющая функцию w(x) > 0 в интервале [a, b], f — процедура, представляющая аппроксимируемую функцию f(х), а и b — числа, задающие интервал аппроксимации [a, b], m и n — степени числителя и знаменателя аппроксимирующей функции, crit — массив, индексированный от 1 до m + n + 2 и представляющий набор оценок в критических точках (то есть точек максимума/минимума кривых погрешности), maxerror — имя переменной, которой присваивается минимаксная норма w abs(f-r). Следующий пример иллюстрирует применение данной функции для аппроксимации функции erf(x): > Digits:=12:w:=proc(х) 1.0 end;w:= proc(x) 1.0 end proc > f:=proc(x) evalf(erf(x)) end;f: = proc(x) evalf (erf (x)) end proc > crit:=array(1..7, [0, .1,.25,.5,.75,.9,1.]);crit := [0, .1, .25, .5, .75, .9, 1.] > remez(w,f,0,1,5,0,crit,'maxerror');x→0.0000221268863 + (1.12678937620 + (0.018447321509 + (-0.453446232421 + (0.141246775527 + 0.00966355213050 x) x) x) x) x > maxerror;0.0000221268894463 5.8.7. Другие функции пакета numapproxОтметим назначение других функций пакета numapprox: chebdeg(p) — возвращает степень полинома Чебышева р; chebmult(p, q) — умножение полиномов Чебышева p и q; chebsort(e) — сортирует элементы ряда Чебышева; confracform(r) — преобразует рациональное выражение r в цепную дробь; confracform(r, х) — преобразует рациональное выражение r в цепную дробь с независимой переменной х; hornerform(r) — преобразует рациональное выражение r в форму Горнера; hornerform(r, х) — преобразует рациональное выражение r в форму Горнера с независимой переменной х; infnorm(f, x=a…b, 'xmax') — возвращает L-бесконечную норму функции на отрезке х[а, b]; infnorm(f, a…b, "xmax") — возвращает L-бесконечную норму функции на отрезке [а, b]. Действие этих функций очевидно и читатель может самостоятельно опробовать их в работе. 5.9. Пакет приближения кривых CurveFitting5.9.1. Общая характеристика пакета Curve FittingПоявившийся еще в Maple 7 пакет приближения кривых CurveFitting весьма полезен тем, кто занимается столь распространенной задачей, как приближение кривых. Он содержит ряд функций: > with(CurveFitting);[BSpline, BSplineCurve, Interactive, LeastSquares, PolynomialInterpolation, RationalInterpolation, Spline, ThieleInterpolation] Доступ к функциям пакета возможен с помощью конструкций: CurveFitting[function](arguments) function(arguments) Число функций пакета невелико и все они описаны ниже. 5.9.2. Функция вычисления В-сплайнов BslineФункция BSpline(k, v, opt) служит для вычисления В-сплайнов. В отличии от обычных сплайнов, у которых точками стыковки сплайн-функций являются узловые точки, В-сплайны позволяют получить стыковку в произвольно заданных точках. Указанная функция имеет следующие параметры: k — порядок сплайна (целое число), v — имя и opt — параметр в виде knots=knotlist, где knotlist — список из k+1 элементов алгебраического типа. Используя функцию CurveFitting[BSplineCurve] можно строить кривые В-сплайнов. Примеры применения этой функции представлены ниже: > BSpline(3, х); 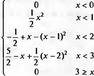 > BSpline(2, х, knots=[0,a,2]);  Как нетрудно заметить из этих примеров, функция Bspline возвращает результат в виде кусочных функций типа piecewise. 5.9.3. Функция построения B-сплайновых кривых BsplineCurveФункция BsplineCurve служит для построения кривых B-сплайнов. Она может использоваться в формах: BSplineCurve(xydata, v, opts) BSplineCurve(xdata, ydata, v, opts) Здесь: xydata — список, массив или матрица точек в форме [[х1,у1],[х2,у2],…,[хn,уn]]; xdata — список, массив или вектор значений независимой переменной [х1,х2,…,хn]; ydata — список, массив или вектор значений зависимой переменной в форме [у1,у2,…,уn]; v — имя независимой переменной; opts — не обязательный параметр в форме одного или более выражений вида order=k или knots=knotlist. Примеры применения функции BSplineCurve с порядком, заданным по умолчанию и с третьим порядком (кубический B-сплайн), представлены на рис. 5.19. Следует отметить, что при малом числе точек стыковки аппроксимация B-сплайнами дает невысокую точность, что хорошо видно из рис. 5.19. 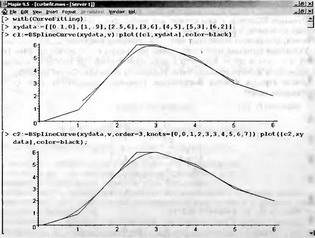 Рис. 5.19. Применение функции BSplineCurve 5.9.4. Сравнение полиномиальной и сплайновой аппроксимацийКогда аппроксимируется гладкая функция, представленная парами данных с равномерным расположением узлом, то данные как полиномиальной, так и сплайновой аппроксимаций различаются незначительно. В этом случае применение куда более сложной сплайновой аппроксимации, как правило, кажется мало обоснованным. Однако если точки данных расположены неравномерно, то применение полиномиальной аппроксимации может оказаться совершенно неприемлемым. Это отчетливо показывает пример, представленный на рис. 5.20. Здесь задана на первый взгляд (судя по расположению точек) не слишком сложная и чуть колебательная зависимость. Однако полиномиальная аппроксимация (представлена тонкой кривой), особенно в начале — в интервале первых трех точек, дает явно ошибочные сильные выбросы. А вот сплайновая аппроксимация (показана более жирном линией) ведет себя куда более приемлемо. 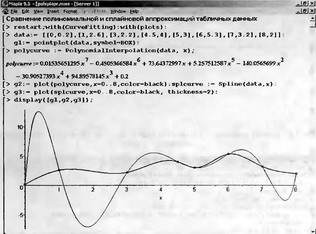 Рис. 5.20. Сравнение полиномиальной и сплайновой аппроксимаций для функции, заданной парами данных при неравномерном расположении узлов Причина лучшего поведения сплайновой аппроксимации здесь вполне очевидна — напоминая поведение гибкой линейки, сплайновая функция эффективно сглаживает выбросы кривой в промежутках между точками. 5.9.5.Сплайновая аппроксимация при большом числе узловПри большом числе узлов (десятки-сотни и выше) данные представленные точками выглядят нередко не представительно. Например, на рис. 5.21 показан документ, иллюстрирующий сплайновую аппроксимацию функции синуса, представленной 31 отсчетом, но без вывода графика сплайновой функции. Несмотря на равномерное расположение узлов по графику точек невозможно определить, что это функция синуса.  Рис. 5.21 Пример представления функции синуса 31 узловыми точками при равномерном расположении узлов Рисунок 5.22 отличается от рис. 5.21 только построением сплайновой функции, представленной графическим объектом g1 (на рис. 5.19 он исключен из параметров функции display). После построения графика сплайновой аппроксимирующей функции становится вполне ясным, что точки представляют функцию синуса, которая прекрасно представляется отрезками полиномов сплайн-функции. 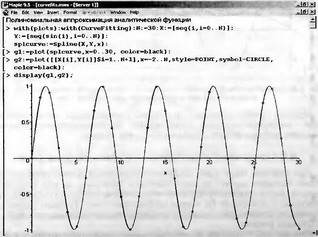 Рис. 5.22. Пример сплайновой аппроксимации синусоидальной функции Здесь полезно обратить внимание на то, что за пределами области узловых точек значения, возвращаемые сплайновой функцией в пакете CurveFitting равны нулю. Так что экстраполяция по ней невозможна (в тоже время функция spline такой возможностью обладает). 5.9.6. Функция реализации метода наименьших квадратов LeastSquaresДо сих пор мы рассматривали методы числовой аппроксимации функций или данных, при которых порядок полиномов определялся числом отсчетов функции. Функция LeastSquares служит для реализации аппроксимации по методу наименьших квадратов. При этом методе происходит статистическая обработка данных (самих по себе или представляющих функцию) исходя из минимума среднеквадратической погрешности для всех отсчетов. Эта функция реализуется в формах: LeastSquares(xydata, v, opts) LeastSquares(xdata, ydata, v, opts) Все входящие в нее параметры были определены выше (см. параметры функции BSplineCurve). Параметр opts задается в форме выражений weight=wlist, curve=f или params=pset. Следующие примеры иллюстрируют применение функции LeastSquares: > with(CurveFitting): LeastSquares([[0,.5], [1,2], [2,4], [3,8]], v);-.050000000000 + 2.44999999999999974 v > LeastSquares([0,1,2,3], [1,2,4,6], v, weight-[1,1,1,10]); 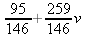 > LeastSquares([0,1,3,5,6], [1,-1,-3,0,5], v, curve=a*v^2+k*v+c); 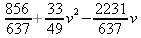 Наглядную иллюстрацию приближения группы точек кривой (в данном случае представленной полиномом четвертой степени) дает рис. 5.23. Кривая в облаке точек располагается таким образом, что площади квадратов над кривой и под ней в сумме равны нулю. 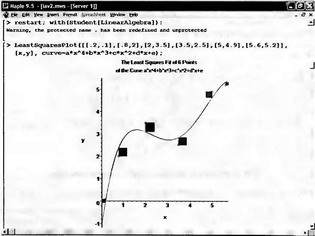 Рис. 5.23. Графическое представление метода наименьших квадратов В конце этой главы мы вернемся к реализации метода наименьших квадратов при выполнении регрессионного анализа, построенного па этом методе. 5.9.7. Функция полиномиальной аппроксимацииФункция Polynomial Interpolation реализует полиномиальную интерполяцию и может использоваться в виде: PolynomialInterpolation(xydata, v) PolynomialInterpolation(xdata, ydata, v) Параметры функции были определены выше. Параметр v может быть как именем, так и численным значением. Примеры применения функции представлены ниже > with(CurveFitting): PolynomialInterpolation([[0,0], [1,2], [2,4], [3, 3]], z); 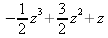 > PolynomialInterpolation([0, 2, 5, 8], [2, a, 1, 3], 3); 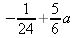 5.9.8. Функция рациональной аппроксимацииФункция рациональной интерполяции задается в виде: RationalInterpolation(xydata, z, opts) RationalInterpolation(xdata, ydata, z, opts) где необязательный параметр opts задается выражениями method=methodtype или degrees=[d1,d2]. Функция возвращает результат в виде отношения двух полиномов. Параметр methodtype может иметь значения lookaround или subresultant, задающие учет или пропуск сингулярных точек. Пример применения функции RationalInterpolation (загрузка пакета опущена, но предполагается): > xpoints := [0,1,2,3,4,-1]: ypoints := [0, 3, 1, 3, а, 1/11]: f := RationalInterpolation(xpoints, ypoints, x); 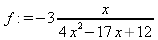 > for i from 1 to 6 do normal(eval(f,x=xpoints[i])-ypoints[i]) end do; 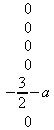 5.9.9. Функция вычисления обычных сплайнов SplineФункция Spline(xydata, v, opts) Spline(xdata, ydata, v, opts) вычисляет обычные (не В-типа) сплайны. Примеры ее применения даны ниже: > Spline([[0,1], [1,2], [2,5], [3,3]], х); 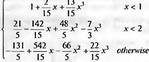 > Spline([0,1,2,3], [1,2,5,3], v, degree=1); 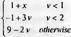 5.9.10. Функция аппроксимации непрерывными дробямиФункция ThieleInterpolation осуществляет интерполяцию на основе непрерывных дробей (Thiele's — интерполяцию). Она задается в виде: ThieleInterpolation(xydata, v) ThieleInterpolation(xdata, ydata, v) Примеры применения данной функции представлены ниже: > ThieleInterpolation([[1,3],[2,5],[4,75],[5,4]], х); 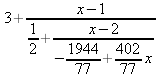 > ThieleInterpolation([1,2,а], [2,4,3], 3) 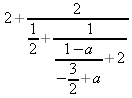 5.10. Выбор аппроксимации для сложной функции5.10.1. Задание исходной функции и построение ее графикаТрудно представить себе область научно-технических расчетов более широкую и почитаемую, чем аппроксимация различных функциональных зависимостей. С получения простой аппроксимации сложной зависимости нередко начинаются (а часто и заканчиваются) научные исследования во многих областях как прикладной, так и фундаментальной науки. Покажем возможности в этом систем Maple на одном из комплексных примеров, давно помещенных в библиотеку пользователей системы Maple V R2, и переработанном для Maple 9.5/10. В этом примере используются многие из описанных выше средств приближения функций. Воспользуемся ранее описанными возможностями пакета numapprox, для чего, прежде всего, подключим его: > restart:with(numapprox): Будем искать приемлемую аппроксимацию для следующей, отнюдь не простой, тестовой функции: > f := х -> int(1/GAMMA(t), t=0..x ) / х^2; 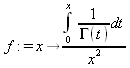 > plot(f,0..4,color=black); График этой функции представлен на рис. 5.24. С первого взгляда это простой график, но тут как раз тот случай, когда простота обманчива. Вы сразу заметите, что график строится медленно, поскольку в каждой из множества его точек системе Maple приходится вычислять значение интеграла с подынтегральной функцией, содержащей довольно каверзную гамма-функцию. И делает это Maple по сложному и медленному алгоритму адаптивного численного интегрирования. 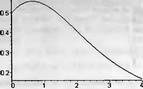 Рис. 5.24. График аппроксимируемой функции Итак, вычисление f(х) по ее интегральному представлению совершенно не эффективно. Наша цель состоит в разработке процедуры вычислений, которая дала бы 6 точных цифр результата в интервале [0..4] и требовала, по возможности, наименьшего числа арифметических операций для каждого вычисления. Втайне не вредно помечтать о том, чтобы после аппроксимации время вычислений уменьшилось бы хотя бы в несколько раз. Что получится на деле, вы увидите чуть позже. А пока войдем в дебри аппроксимации. 5.10.2. Аппроксимации рядом ТейлораНачнем с аппроксимации функции хорошо известным рядом Тейлора степени 8 относительно середины интервала (точки с х=2): > s := map(evalf, taylor(f(x), х=2, 9));s := 0.4065945998 - 0.1565945998(x-2) + 0.00209790791(х-2)2 + 0.01762626393(х-2)3 - 0.006207547150(x-2)4 + 0.00057335662(x-2)5 + 0.00024331163(x-2)6 - 0.00010010534(x-2)7 + 0.00001414211(х-2)8 + O((x-2)9) > TaylorApprox := convert(s, polynom): Такой ряд позволяет использовать для вычислений только арифметические действия, что само по себе здорово! Для удобства преобразуем аппроксимацию в функцию, чтобы она соответствовала форме, указанной для первоначальной функции f(х). Тогда мы сможем построить график кривой ошибок для аппроксимации полиномом Тейлора: > TaylorApprox := unapplу(TaylorApprox, х);TaylorApprox := x→0.7197837994 - 0.1565945998x + 0.00209790791(x-2)2 + 0.01762626393(x-2)3 - 0.006207547150(x-2)4 + 0.00057335662(x-2)5 + 0.00024331162(x-2)6 - 0.00010010534(x-2)7 + 0.0000141421(x-2)8 Кривая ошибок для аппроксимации полиномом Тейлора строится командой > plot(f - TaylorApprox, 0..4, color=black); и имеет вид, представленный на рис. 5.25. Эта кривая нас, прямо скажем, не слишком радует, поскольку погрешность в сотни раз превышает заданную.  Рис. 5.25. Кривая погрешности при аппроксимации рядом Тейлора Типичное свойство аппроксимации рядом Тейлора состоит в том, что ошибка мала вблизи точки разложения и велика вдали от нее. В данном случае, самая большая ошибка имеет место в левой оконечной точке. Чтобы вычислить значение ошибки в точке х=0, что ведет к делению на нуль (см. определение для f(х)), мы должны использовать значение предела: > maxTaylorError := abs(limit(f(x), х=0) - TaylorApprox(0));maxTaylorError := 0.0015029608 Итак, в самом начале наших попыток мы потерпели полное фиаско, получив совершенно неприемлемое значение погрешности в сотни раз больше заданной. Но отчаиваться не стоит, ибо, как говорят, «даже у хорошей хозяйки первый блин — комом». 5.10.3. Паде-аппроксимацияТеперь опробуем рациональную аппроксимацию Паде (Pade) функции f(x) степени (4,4). Приближения, по этому разложению, будут аппроксимировать функцию более точно, и потому ошибки округления в вычислениях станут более заметными. Поэтому зададим вычисления с двумя дополнительными знаками точности: > Digits := 12: > s := map(evalf, taylor(f(x), x=2, 9)): > PadeApprox := pade(s, x=2, [4,4]);PadeApprox := (0.341034792604 + 0.0327799035348x - 0.00612783638188(x-2)2 + 0.00452991113636(x-2)3 - 0.000431506338862(x-2)4)/( 0.068484906786 + 0.465757546607x+ 0.159149610837(x-2)2 + 0.0266813683828(x-2)3 + 0.00346967791444(x-2)4) > PadeApprox := unapply(PadeApprox, x): Кривая ошибки для интервала [0,4] строится командой > plot(f - PadeApprox, 0..4,color=black); и имеет вид, показанный на рис. 5.26.  Рис. 5.26. Кривая погрешности при Паде-аппроксимации степени (4.4) Как и при аппроксимации рядом Тейлора, ошибка здесь мала вблизи точки разложения и велика вдали от нее. Мы снова видим из графика, что для указанной функции, самая большая ошибка — в левой оконечной точке. Однако, максимальная ошибка в Паде-аппроксимации уже на порядок меньше, чем при аппроксимации полиномом Тейлора: > maxPadeError := abs(limit(f(x), x=0) - PadeApprox(0));maxPadeError:=0.000353777322 Это успех, показывающий, что мы на верном пути. Но, пока, погрешность остается слишком большой по сравнению с заданной. 5.10.4. Аппроксимация полиномами ЧебышеваЗнатоки техники аппроксимации знают, что лучшие приближения на заданном интервале могут быть получены, используя разложение в ряд Чебышева. Это связано с тем, что ортогональные полиномы Чебышева позволяют получить аппроксимацию, погрешность которой в заданном диапазоне изменения аргумента распределена более равномерно, чем в предшествующих случаях. Выбросы погрешности на краях интервала аппроксимации в этом случае исключены Разложим функцию f(x) на [0,4] в ряд Чебышева с точностью 1*10-8. Это означает, что все члены с коэффициентами меньше, чем эта величина, будут опущены. Такая точность обеспечивается полиномом 13 степени: > evalf(limit(f(x), х=0));.500000000000 > fproc := proc(x) if x=0 then 0.5 else evalf(f(x)) fi end: > ChebApprox := chebyshev(fproc, x=0..4, 1E-8); 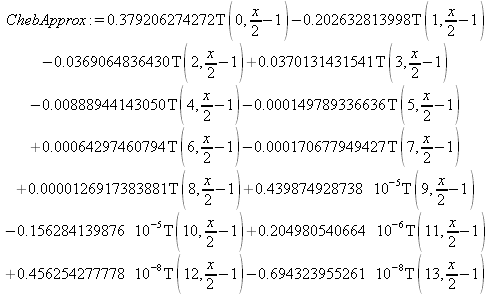 Можно проверить для этого примера, что кривая ошибки при аппроксимации рядом Чебышева колеблется. Поскольку ряд Чебышева был оборван на члене степени 8 (как и полином ряда Тейлора), то максимальная ошибка оказалась все еще больше заданной. Для последующих вычислений, полезно заметить, что мы можем использовать процедуру для нахождения численных значений f(x), которая будет намного эффективнее, чем прямое определение, которое требует численного интегрирования для каждого значения х. А именно, определим процедуру численной оценки, основанную на разложении в ряд Чебышева степени 13, так как максимальная ошибка при такой аппроксимации меньше, чем 10-8, и обеспечивает для нашей цели достаточную точность. Мы определим полином Чебышева Т(х) из пакета orthopoly, и затем для эффективной оценки преобразуем его в форму Горнера: > F := hornerform(eval(subs(T=orthopoly[T], ChebApprox)));F = 0.499999998610 + (0.192405358503 + (-0.163971754264 + (-0.0083861432817 + (0.0277082269676 + (-0.00593172541573 + (-0.00132728874257 + (0.000910057654178 + (-0.000180351181100 + (0.57685696534 10-5 + ( 0.448885653549 10-5 + (-0.990274556116 10-6 + (0.925433855729 10-7 - 0.347161977631 10-8x)x)x)x)x)x)x)x)x)x)x)x)x > F := unapply(F, x): Схема Горнера минимизирует число арифметических операций, заменяя операции возведения в степень операциями последовательного умножения. 5.10.5. Аппроксимация Чебышева-ПадеТеперь рассмотрим еще более точную рациональную аппроксимацию Чебышева-Паде. Это такая рациональная функция r[m, n](х) с числителем степени m и знаменателем степени n такой же, как и для разложения в ряд Чебышева. Функция r[m, n](х) согласуется с разложения в ряд ряда Чебышева f(x) членом степени m+n. Мы вычислим аппроксимацию Чебышева-Паде степени (4, 4), подобную обычной Паде-аппроксимации, успешно выполненной ранее: > ChebPadeApprox := chebpade(F, 0..4, [4,4]); 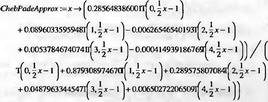 Построим кривую ошибок: > with(orthopoly, Т): > plot(F - ChebPadeApprox, 0..4,color=black); Она представлена на рис. 5.27. 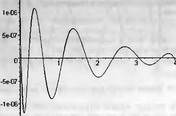 Рис. 5.27. Кривая ошибки при Паде-Чебышева рациональной аппроксимации Максимальная ошибка и на этот раз имеет место в левой оконечной точке. Величина максимальной ошибки несколько меньше, чем ошибка при аппроксимации рядом Чебышева. Главное преимущество преставления в виде рациональной функции — высокая эффективность вычислений, которая может быть достигнута преобразованием в непрерывную (цепную) дробь (см. ниже). Однако полученная максимальная ошибка чуть-чуть больше заданной: > maxChebPadeError := abs(F(0) - ChebPadeApprox(0));maxChebPadeError := 0.1236749 10-5 Мы достигли впечатляющего успеха и остается сделать еще один шаг в направлении повышения точности аппроксимации. 5.10.6. Минимаксная аппроксимацияКлассический результат теории аппроксимации заключается в том, что минимакс как наилучшая аппроксимация рациональной функции степени (m, n) достигается, когда кривая ошибки имеет m+n+2 равных по величине колебаний. Кривая ошибки аппроксимации Чебышева-Паде имеет нужное число колебаний, но эта кривая должна быть выровнена (по амплитуде выбросов кривой ошибки) с тем, чтобы обеспечить наилучшее минимаксное приближение. Эта задача решается с помощью функции minimax: > MinimaxApprox := minimax(F, 0..4, [4,4], 1, 'maxerror');MinimaxApprox :=x→ (0.174933018974 + (0.0833009600964 + (-0.02019330447644 + (0.00368158710678 - 0.000157698045886x)x)x)x)/(0.349866448284 + (0.031945251383 + (0.0622933780130) + (-0.0011478847868 + 0.0033634353802x)x)x)x) Максимальная ошибка в аппроксимации MinimaxApprox дается значением переменной maxerror. Заметим, что мы, наконец, достигли нашей цели получения аппроксимации с ошибкой меньшей, чем 1*10-6: > maxMinimaxError := maxerror;maxMinimaxError := 0.585028048949 10-6 Построим график погрешности для данного типа аппроксимации: > plot(F - MinimaxApprox,0..4,color=black); График ошибки, представленный на рис. 5.28 показывает равные по амплитуде колебания. 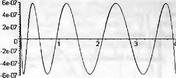 Рис. 5.28. График ошибки при минимаксной аппроксимации Таким образом, мы блестяще добились успеха в снижении погрешности до требуемого и довольно жесткого уровня. Если бы мы задались целью получить только четыре или пять точных знаков аппроксимации, что в целом ряде случаев вполне приемлемо, то могли бы получить нужный результат гораздо раньше. Нам остается оптимизировать полученную аппроксимацию по минимуму арифметических операций и проверить реальный выигрыш по времени вычислений. 5.10.7. Эффективная оценка рациональных функцийПолиномы числителя и знаменателя в минимаксной аппроксимации уже выражены в форме Горнера (то есть в форме вложенного умножения). Оценка полиномом степени n в форме Горнера при n умножениях и n суммированиях это наиболее эффективная схема оценки для полинома в общей форме. Однако, для рациональной функции степени (m, n) мы можем делать кое-что даже лучше, чем просто представить выражения числителя и знаменателя в форме Горнера. Так, мы можем нормализовать рациональную функцию так, что полином знаменателя со старшим коэффициентом будет равным 1. Мы можем также заметить, что вычисление рациональной функции степени (m, n) в форме Горнера требует выполнения всего m+n сложений, m+n-1 умножений и 1 деления. Другими словами, общий индекс действия есть m + n операций умножения/деления, m + n операций сложения/вычитания. Вычисление рациональной функции можно значительно сократить и далее, преобразуя ее в непрерывную (цепную) дробь. Действительно, рациональная функция степени (m, n) может быть вычислена, используя только max(m, n) операций умножения/деления, m + n операций сложения/вычитания. Например, если m = n, тогда эта новая схема требует выполнения только половины числа действий умножения/деления по сравнению с предшествующим методом. Для рациональной функции MinimaxApprox, вычисление в форме, выраженной выше, сводится к 9 действиям умножения/деления и 8 действиям сложения/вычитания. Число операций умножения/деления можно сократить до 8, нормализуя знаменатель к форме monic. Мы можем теперь вычислить непрерывную (цепную) дробь для той же самой рациональной функции. Вычисление по этой схеме, как это можно видеть из вывода Maple, сводятся только 4 действиям деления и 8 действиям сложения/вычитания: > MinimaxApprox := confracform(MinimaxApprox): > lprint(MinimaxApprox(x)); -.468860043555e-1 + 1.07858988373/ (x+4.41994160718+16.1901836591/(x+4.29118998064+70.1943521765/(x-10.2912531257+4.77538954280/(x+1.23883810079)))) 5.10.8. Сравнение времен вычисленийТеперь определим время, необходимое для вычисления функции f(x) в 1000 точек, используя первоначальное интегральное определение, и сравним его с временем, требующимся для схемы MinimaxApprox в виде непрерывной дроби. Сделаем это для системы Maple 8. Так как наше приближение будет давать только 6 точных цифр, мы также потребуем 6 точных цифр и от интегрального представления функции: > Digits := 6: st := time(): > seq( evalf(f(i/250.0) ) , i = 1..1000 ): > oldtime := time() - st;oldtime := 4.075 В процессе вычислений с использованием представления рациональной функции в виде непрерывной дроби иногда требуется внести несколько дополнительных цифр точности для страховки. В данном случае достаточно внести две дополнительные цифры. Итак, новое время вычислений: > Digits := 6: st := time(): > seq( MinimaxApprox(i/250.0), i = 1..1000 ): > newtime := time() - st;newtime := 0.342 Ускорение вычисления при аппроксимации есть: > SpeedUp := oldtime/newtime;SpeedUp := 11.915205 Мы видим, что процедура вычислений, основанная на MinimaxApprox, выполняется почти в 12 раз быстрее процедуры с использованием исходного интегрального определения. Это серьезный успех, полностью оправдывающий время, потерянное на предварительные эксперименты по аппроксимации и ее оптимизации! Заметим, что этот результат относится только к конкретному ПК и может сильно меняться при прогонке этого примера на других. Так, читатель, знакомый с учебным курсом автора по системе Maple 7 [36] обнаружит, что там в этом примере результаты были иные и куда более ошеломляющие: oldtime := 81.805 newtime := .694 SpeedUp := 117.87464В чем дело? А дело в том, что более ранние результаты были получены в среде Maple 7 на компьютере с процессором Pentium II с частотой 400 МГц. А новые результаты получены уже на компьютере с процессором Pentium 4 с частотой 2,6 ГГц и с системой Maple 9.5. 5.10.9. Преобразование в код ФОРТРАНа или СОдин из поводов разработки эффективной аппроксимации для вычисления математической функции заключается в создании библиотек подпрограмм для популярных языков программирования высокого уровня, таких как ФОРТРАН или С. В Maple имеются функции преобразования на любой из этих языков. Например, мы можем преобразовывать формулу для минимаксной аппроксимации в код ФОРТРАНа: > fortran (MinimaxApprox(х));  Итак, нами показано, что правильный выбор аппроксимации для сложной функции обеспечивает уменьшение времени ее вычисления более чем на один-два порядка (!) при весьма приличной точности в 6 верных знаков и при использовании для вычислений минимального числа арифметических операций. Применение при этом средств системы Maple позволяет генерировать разложения в различные ряды, быстро вычислять рациональные аппроксимации функций и выполнять преобразования в различные специальные формы, сочетая это с мощными средствами интерактивной работы и графической визуализации, в частности с построением графиков функции и кривых ошибок при разных видах аппроксимации. Все это обеспечивает идеальную среду для решения таких задач. 5.11. Интегральные преобразования функций5.11.1. Прямое и обратное Z-преобразованияИнтегральные преобразования (см. файл inttrans) широко применяются в науке и технике. Так, прямое и обратное Z-преобразования функций широко используются при решении задач автоматического управления и обработке дискретных сигналов. Прямое Z-преобразование последовательности f(n) в функцию комплексной переменной z задается выражением: 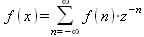 Обратное Z-преобразование сводится к преобразованию комплексной функции f(z) в функцию f(z). Эти преобразования задаются следующими функциями: ztrans(f, n, z) — прямое преобразование функции f(n) в f(z); invztrans(f, z, n) — обратное преобразование f(z) в f(n). Заметим, что прямое Z-преобразование базируется на соотношении ztrans(f(n),n,z)=sum(f(n)/z^n,n=0..infinity), записанном на Maple-языке. В первых версиях системы Maple Z-преобразования выполнялись средствами библиотеки и требовали вызова командой readlib(ztrans). Но в Maple 7/8 они уже были включены в ядро системы и предварительного вызова уже не требуют. В этом убеждают следующие примеры: > a:=ztrans(n^2,n,z); 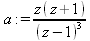 > invztrans(a,z,n);n² > ztrans(cos(Pi/4*t), t, z); 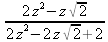 > invztrans(%,z,t); 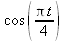 Нетрудно заметить, что в этих примерах функции, после прямого и обратного преобразований, восстанавливают свои значения. 5.11.2. Быстрое преобразование ФурьеПреобразование Фурье широко используется в математике, физике и электрорадиотехнике. Суть этого преобразования описана чуть ниже — см. раздел 5.11.4. Ввиду широких сфер применения этого преобразования в технике часто используется его особая разновидность — быстрое преобразование Фурье или FFT (Fast Fourier Transform). В Maple на уровне ядра реализованы функции быстрого прямого FFT и обратного iFFT преобразований Фурье для числовых данных: FFT(m, х, у) evalhf(FFT(m, var(x), var(y))) iFFT(m, x, y) evalhf(iFFT(m, var(x), var(y))) Здесь m — целое неотрицательное число, х и у — массивы с числом элементов, кратным степени 2 (например 4, 8, 16 и т.д.), представляющие действительные и мнимые части массива комплексных чисел (данных). Функции возвращают число элементов выходных массивов, а результат преобразований помещается в исходные массивы: > х := array([1.,2.,3.,4.]): у := array([5.,6.,7.,8.]): > FFT(2,х,y);4 > print(х);[10., -4., -2., 0.] > print(y);[26., 0., -2., -4.] > iFFT(2,х,y);4 > print(x);[1.0000000, 2.0000000, 3.0000000, 4.0000000] > print(y);[5.0000000, 6.0000000, 7.0000000, 8.0000000] Несмотря на высокую эффективность быстрых преобразований Фурье их недостатком является применение только к дискретно заданным численным данным, причем с числом отсчетов кратным двум в целой степени. Если данных меньше, недостающие элементы обычно заменяются нулями. Альтернативой преобразований Фурье в наши дни стали вейвлет-преобразования. Вейвлеты это новый обширный базис для приближения произвольных зависимостей вейвлетами — «короткими» волночками разной формы, способными к масштабированию и перемещению. Вейвлеты прекрасно подходят для приближения локальных особенностей различных зависимостей, в том числе нестационарных (с параметрами, меняющимися во времени). Ознакомиться с вейвлетами и средствами работы с ними в системах MATLAB, Mathematica и Mathcad можно по книге [55]. К сожалению, в Maple готовые средства вейвлет-преобразований отсутствуют и это серьезный недостаток этих систем. 5.11.3. Общая характеристика пакета inttransДля расширенной поддержки интегральных преобразований служит пакет inttrans Это один из пакетов, наиболее важных для общематематических и научно-технических приложений. Он вызывается командой > with(inttrans);[addtable, fourier, fouriercos, fouriersin, hankel, hilbert, invfourier, invhilbert, invlaplace, invmellin, laplace, mellin, savetable] и содержит небольшой набор функций. Однако эти функции охватывают такие практические важные области математики, как ряды Фурье, прямые и обратные преобразования Лапласа и Фурье и ряд других интегральных преобразований. Ниже они обсуждены более подробно. 5.11.4. Прямое и обратное преобразование ФурьеПрямое преобразование Фурье преобразует функцию времени f(t) в функцию частот F(w) и заключается в вычислении следующей интегральной функции: 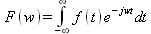 Оно в аналитическом виде реализуется следующей функцией пакета интегральных преобразований inttrans: fourier(expr, t, w) Здесь expr — выражение (уравнение или множество), t — переменная, от которой зависит expr, и w — переменная, относительно которой записывается результирующая функция. Обратное преобразование Фурье задается вычислением интеграла 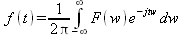 Оно фактически переводит представление сигнала из частотной области во временную. Благодаря этому преобразования Фурье удобны для анализа прохождения воздействий (сигналов) si(t) через устройства (цепи), заданные их частотной характеристикой K(w): si(t)→fourier→s(w)→s(w)∙K(w)→invfourier→so(t).Здесь si(t) и so(t) — временные зависимости соответственно входного и выходного сигналов. Определение (визуализация) преобразований Фурье и примеры их осуществления представлены ниже: > restart:with(inttrans): assume(lambda>0,а>0): > convert(fourier(f(t), t, s), int); 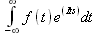 > convert(invfourier(f(t),t,s),int);  > fourier(sin(t),t,w);-I π Dirac(w - 1) + I π Dirac(w + 1) > invfourier(%,w,t);sin(t) > fourier(1-exp(-a*t),t,w);2 π Dirac(w) - fourier(e(-at),t,w) > invfourier(%,w,t);1 - e(-at) > fourier(ln(1/sqrt(1+x^2)),x,y); 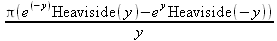 > fourier(BesselJ(n,x),x,y); 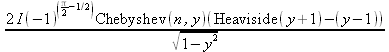 5.11.5. Вычисление косинусного и синусного интегралов ФурьеРазложение функции f(t) в ряд Фурье требует вычисления интегралов следующего вида: 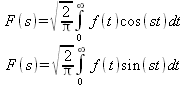 Они получили название косинусного и синусного интегралов Фурье и фактически задают вычисление коэффициентов ряда Фурье, в который может быть разложена функция f(t). Для вычисления этих интегралов в пакете используются следующие функции: fouriercos(expr,t,s) fouriersin(expr,t,s) Поскольку формат задания этих функций вполне очевиден, ограничимся примерами визуализации сути этих функций и примерами их применения: > convert(fouriercos(f(t),t,s),int); 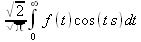 > convert(fouriersin(f(t),t,s),int); 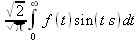 > fouriercos(5*t,t,s); 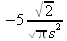 > fouriersin(5*t,t,s); > fouriercos(exp(-t),t,s); 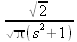 > fouriercos(arccos(х) * Heaviside(1-х), х, y); 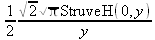 > fouriersin(arcsin(x) * Heaviside(1-х), x, y); 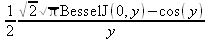 Нетрудно заметить, что эти преобразования нередко порождают специальные математические функции. Много примеров на преобразования Фурье содержатся в файле демонстрационных примеров fourier.mws. 5.11.6. Прямое и обратное преобразование ЛапласаПреобразования Лапласа — одни из самых часто применяемых интегральных преобразований. Они широко применяются в электрорадиотехнике и часто используются для решения линейных дифференциальных уравнений. Прямое преобразование Лапласа заключается в переводе некоторой функции времени f(t) в операторную форму F(p). Это преобразование означает вычисление интеграла 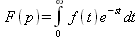 Для осуществления прямого преобразования Лапласа служит функция laplace(expr,t,р) Здесь expr — преобразуемое выражение, t — переменная, относительно которой записано expr, и p — переменная, относительно которой записывается результат преобразования. Обратное преобразование Лапласа означает переход от функции F(p) к функции f(t) с помощью формулы 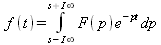 Для вычисления этого интеграла служит функция invlaplace(expr, р, t) где expr — выражение относительно переменной p, t — переменная, относительно которой записывается результирующая зависимость. Оба преобразования широко применяются в практике научно-технических вычислений и отражают суть операторного метода. При этом прямое преобразование создает изображение, а обратное — оригинал функции. Ниже приведены примеры определения и применения прямого и обратного преобразований Лапласа: > restart:with(inttrans): > convert(laplace(f(t),t,s), int); 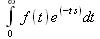 > laplace(sin(t)+a*cos(t),t,p); 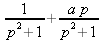 > invlaplace(%,р,t);sin(t) + a cos(t) Нетрудно заметить, что в данном случае последовательное применение прямого, а затем обратного преобразования восстанавливает исходную функцию sin(t)+a cos(t). Преобразования Лапласа широко используются со специальными функциями и, в свою очередь, порождают специальные функции: > laplace(FresnelC(t),t,p); 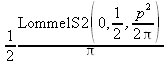 > laplace(Si(t)+Ci(t)+erf(t),t,p); 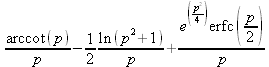 > laplace(BesselJ(0,t),t,p); 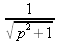 > invlaplace(1/sqr(р^2+1),t,р); 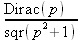 Преобразования Лапласа широко используются для решения линейных дифференциальных уравнений в аналитическом виде. Ниже дана пара простых примеров, иллюстрирующих технику такого решения для дифференциальных уравнений второго порядка с применением функции dsolve: > de1 := diff(y(t),t$2) + 2*diff(y(t),t) + 3*y(t) = 0; 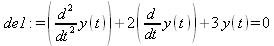 > dsolve({del,y(0)=0,D(y)(0)=1},y(t),method=laplace); 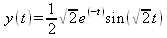 > de2 := diff(y(х),х$2) - y(х) = x*cos(x); 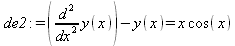 > dsolve({de2,y(0)=0,D(y)(0)=0},y(x), method=laplace); 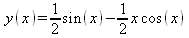 Множество примеров на применение преобразования Лапласа можно найти в файле laplace.mws, имеющимся на Интернет-сайте корпорации MapleSoft. 5.11.7. Интегральное преобразование ХанкеляИнтегральное преобразование Ханкеля задается следующим выражением: 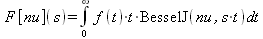 и выполняется функцией hankel(expr, t, s, nu) Здесь expr — выражение, равенство (или множество, или список с выражениями/равенствами), t — переменная в expr, преобразуемая в параметр преобразования s, nu — порядок преобразования. Следующий пример демонстрирует вывод и применения функции Ханкеля: > convert(hankel(f(t), t, s, v), int); 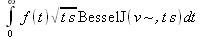 > hankel(sqrt(t)/(alpha+t), t, s, 0); 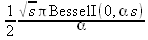 > hankel(sqrt(t)*Ci(alpha*t^2),t,s,0); 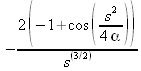 > hankel(1/sqrt(t)*erfс(alpha*t),t,s,0); 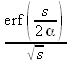 > assume(-1/2<mu,mu<1/2); hankel(1/sqrt(t)*BesselY(mu,alpha/t),t,s,mu); 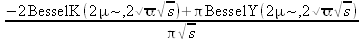 > hankel(t^(1/3), t, s, 2); 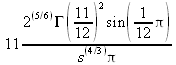 5.11.8. Прямое и обратное преобразования ГильбертаПрямое преобразование Гильберта задается следующим выражением: 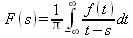 и превращает функцию f(t) в F(s). Обратное преобразование Гильберта означает нахождение f(t) по заданной F(s). Эти преобразования выполняются функциями: hilbert(expr, t, s) invhilbert(expr, t, s) где назначение параметров очевидно. Приведенные ниже примеры иллюстрируют выполнение этих преобразований: > restart:with(inttrans): > assume(-1/2<v,v<3/2,nu>0,a>0,alpha>0,beta>0): > convert(hilbert(f(t),t,s), int); 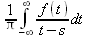 > convert(invhilbert(f(t),t,s),int); 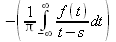 > hilbert(exp(1), r, z);0 > hilbert(f(u), u, t);hilbert(f(w), u, t) > hilbert(%, t, s);-f(s) > hilbert(t*f(t), t, s); 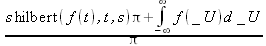 > hilbert(t/(t^2+1),t,s); 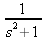 > invhilbert(%,s,t); 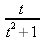 > hilbert(sin(x)/x,x,y); 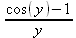 > hilbert(%,y,2);-ln(I Z) > hilbert(Ci(abs(t)),t,s);-signum(s) Ssi(|s|) > hilbert(signum(t)*Ssi(abs(t)),t,s);Ci(|s|) > hilbert(t*f(a*t)^2,t,s); 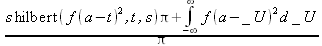 Как видно из этих примеров, обратное преобразование Гильберта, осуществленное над результатом прямого преобразования, не всегда восстанавливает функцию f(t) буквально. Иногда преобразование Гильберта (см. последний пример) выражается через само себя. Много интересных примеров на это преобразование Гильберта можно найти в файле gilbert.mws. 5.11.9. Интегральное преобразование МеллинаИнтегральное преобразование Меллина задается выражением 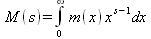 и реализуется функцией mellin(expr, x, s) с очевидными параметрами expr, x и s. Применение преобразования Меллина иллюстрируют следующие примеры: > assume(а>0); > mellin(x^a,x,s); 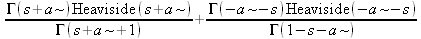 > mellin(f(а*х),х,s); mellin(f(a*x), x, s); 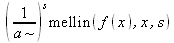 > invmellin((gamma+Psi(1+s))/s,s,x,-1..infinity);-Heaviside(1-x)ln(1-x) Примеры на применение преобразования Меллина можно найти в файле mellin.mws. 5.11.10. Функция addtableКак видно из приведенных примеров, не всегда интегральные преобразования дают результат в явном виде. Получить его позволяет вспомогательная функция addtable(tname,patt,expr,t,s) где tname — наименование преобразования, для которого образец patt должен быть добавлен к таблице поиска. Остальные параметры очевидны. Следующие примеры поясняют применение этой функции: > fouriersin(f(t),t,s);fouriersin(f(t), t, s) > addtable(fouriersin,f(t),F(s), t,s); > fouriersin(f(x),x,2);F(z) 5.12. Регрессионный анализ5.12.1. Функция fit для регрессии в пакете statsВ этой главе до сих пор рассматривались точные функции преобразования или представления аналитических функций. Однако часто возникает и другая задача — некоторую совокупность данных, например заданных таблично, надо приближенно представить некоторой известной аналитической функцией. Эта задача решается регрессионным анализом или просто регрессией. Параметры приближающей функции выбираются так, что она приближенно (по критерию минимума среднеквадратической ошибки) аппроксимирует исходную зависимость. Последняя, чаще всего, бывает представлена некоторым набором точек (например, полученных в результате эксперимента). Наглядная визуализация регрессии была рассмотрена выше — см. рис. 5.23. А теперь рассмотрим типовые средства проведения регрессии (файл regres). Для проведения регрессионного анализа служит функция fit из пакета stats, которая вызывается следующим образом: stats[fit,leastsquare[vars,eqn,parms]](data) или fit[leastsquare[vars,eqn,parms]](data) где data — список данных, vars — список переменных для представления данных, eqn — уравнение, задающее аппроксимирующую зависимость (по умолчанию линейную), parms — множество параметров, которые будут заменены вычисленными значениями. 5.12.2. Линейная и полиномиальная регрессия с помощью функции fitНа приведенных ниже примерах показано проведение регрессии с помощью функции fit для зависимостей вида у(х): > with(stats):Digits:=5;Digits := 5 > fit[leastsquare[[x,у]]] ([[1, 2, 3, 4], [3, 3.5, 3.9, 4.6]] );у = 2.4500 + .52000 x > fit[leastsquare[[x,y, y=a*x^2+b*x+c]] ([[1,2,3,4], [1.8,4.5,10,16.5]]);у = 0.9500000000 x² + 0.2100000000 x + 0.5500000000 В первом примере функция регрессии не задана, поэтому реализуется простейшая линейная регрессия, а функция fit возвращает полученное уравнение регрессии для исходных данных, представленных списками координат узловых точек. Это уравнение аппроксимирует данные с наименьшей среднеквадратичной погрешностью. Во втором примере задано приближение исходных данных степенным многочленом второго порядка. Вообще говоря, функция fit обеспечивает приближение любой функцией в виде полинома, осуществляя полиномиальную регрессию. Рисунок 5.29 показывает регрессию для одних и тех же данных полиномами первой, второй и третьей степени с построением их графиков и точек исходных данных. 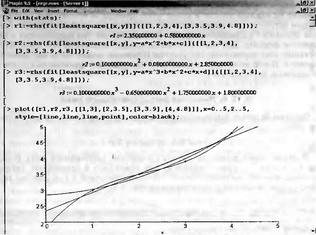 Рис. 5.29. Примеры регрессии полиномами первой, второй и третьей степени Нетрудно заметить, что лишь для полинома третьей степени точки исходных данных точно укладываются на кривую полинома, поскольку в этом случае (4 точки) регрессия превращается в полиномиальную аппроксимацию. В других случаях точного попадания точек на линии регрессии нет, но обеспечивается минимум среднеквадратической погрешности для всех точек — следствие реализации метода наименьших квадратов. Применение регрессии обычно оправдано при достаточно большом числе точек исходных данных. При этом регрессия может использоваться для сглаживания данных. 5.12.3. Регрессия для функции ряда переменныхФункция fit может обеспечивать регрессию и для функций нескольких переменных. При этом надо просто увеличить размерность массивов исходных данных. В качестве примера ниже приведен пример регрессии для функции двух переменных > f:=fit[leastsquare[[x, у, z],z=a+b*x+c*y,{a,b,c}]]\ ([[1,2,3,5,5], [2,4,6,8,8], [3, 5, 7,10, Weight (15, 2)]]) ;f := z = 1 + 13/3 x - 7/6 у > fa:=unapply(rhs(f),x,у);fa := (x, y) -> 1 + 13/3 x - 7/6 у > fa(l., 2.) ;2.999999999 > fa(2,3);37/6 В данном случае уравнение регрессии задано в виде z = а + bх + су. Обратите внимание на важный момент в конце этого примера — применение полученной функции регрессии для вычислений или построения ее графика. Прямое применение функции f в данном случае невозможно, так как она представлена в невычисляемом формате. Для получения вычисляемого выражения она преобразуется в функцию двух переменных fa(x,y) путем отделения правой части выражения для функции f. После этого возможно вычисление значений функции fa(x,y) для любых заданных значений х и у. 5.12.4. Линейная регрессия общего видаФункция fit может использоваться и для выполнения линейной регрессии общего вида: f(x) = af1(x) +bf2(x) +cf3(x) + …Функция такой регрессии является линейной комбинацией ряда функций f1(х), f2(х), f3(х), причем каждая их них может быть и нелинейной, например экспоненциальной, логарифмической, тригонометрической и т.д. Пример линейной регрессии общего вида представлен на рис. 5.30. 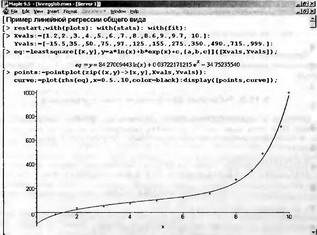 Рис. 5.30. Пример выполнения линейной регрессии общего вида В литературе и даже в документах системы Maple линейная регрессия общего вида часто называется нелинейной регрессий. Однако это неверно, поскольку нелинейной является регрессия, функция которой не может быть представлена линейной комбинацией функций. 5.12.5. О нелинейной регрессии с помощью функции fitК сожалению, функция fit неприменима для нелинейной регрессии. При попытке ее проведения возвращается структура процедуры, но не результат регрессии — см. пример ниже: > fit[leastsquare[[х,у], у=а*2^(х/b),{а,b}]]([[1,2,3,4], [1.1,3.9,9.5,15.25]]); 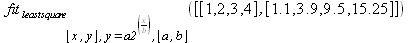 Однако, большинство нелинейных зависимостей удается свести к линейным с помощью простых линеаризирующих преобразований [1, 2, 4]. На рис. 5.31 показан пример экспоненциальной регрессии f(x)=аеbх, которая (благодаря логарифмированию точек y) сводится к линейной регрессии. Детали преобразований даны в документе рис. 5.31. Используя другие преобразования этот документ легко приспособить для выполнения других видов нелинейной регрессии, например степенной или логарифмической. 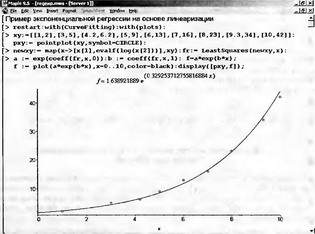 Рис. 5.31. Пример экспоненциальной регрессии Функция нелинейной регрессии входит в новейший пакет оптимизации Optimization, введенный в Maple 9.5, и описанный в следующей главе. Кроме того, на Интернет-сайте корпорации Waterloo Maple можно найти файлы simplenl.mws и gennlr.mws с процедурами и примерами линейной и нелинейной регрессий общего вида. Интересная реализация нелинейной регрессии для кусочной функции дается в файле nonelinearpiecewise.mws. 5.12.6. Сплайновая регрессия с помощью функции BSplineCurveФункция BSplineCurve из пакета CurveFitting может использоваться для реализации сплайновой регрессии. Пример этого представлен на рис. 5.32. Опция order задает порядок B-сплайнов, который на 1 меньше заданного целого значения. 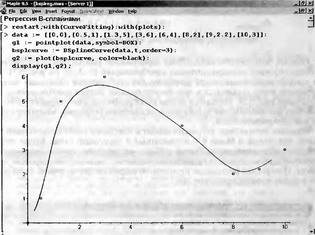 Рис. 5.32. Пример выполнения сплайновой регрессии В-сплайнами Функция BsplineCurve выглядит несколько недоделанной. Так, при order=3 и 4 кривая регрессии не дотягивает до концевых точек, а при установки order=1 все точки соединяются отрезками прямых — в том числе концевые. Так что использовать эту функцию для экстраполяции нельзя. 5.13. Работа с функциями двух переменных5.13.1. Maplet-инструмент для работы с функциями двух переменныхДля эффектной демонстрации работы с функциями многих переменных в состав пакета Student системы Maple 9.5 введен новый подпакет MultivariateCalculus. Его примеры можно запускать как с командной строки, так и из позиции Tools меню в стандартном варианте интерфейса — Tutors→Calculus→Calculus-Multi-Variables. Approximate Integration… — открывает Maplet-окно аппроксимации двойных интегралов; Cross Section… — открывает Maplet-окно демонстрации сечения поверхности; Directional Derivatives… — открывает Maplet-окно вычисления производных в заданном направлении; Gradient… — открывает Maplet-окно вычисления градиента; Taylor Series… — открывает Maplet-окно разложения функций в ряд Тейлора. Представленные средства носят учебный характер — не случайно они входят в пакет Student. Реально визуализация возможна только для функций двух переменных. 5.13.2. Демонстрация разложения в ряд Тейлора функции двух переменныхКоманда Taylor Series… — открывает Maplet-окно разложения функции двух переменных z(х, у) в ряд Тейлора относительно заданной точки (х0, у0). Это окно представлено на рис. 5.33. 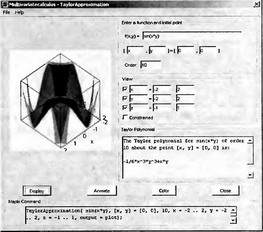 Рис. 5.33. Maplet-окно демонстрации разложения в ряд Тейлора функции двух переменных В данном окне дан пример разложения в ряд Тейлора функции sin(x*y) в окрестности точки (0, 0) в интервале изменения х[-2, 2], у[-2, 2] и z[-1, 1]. Установки в окне совершенно очевидны. Графики в правой части представляют поверхность, описываемую исходной функцией и поверхность, представленную рядом Тейлора. Кнопка Display начинает построение графиков, кнопка Animation позволяет наблюдать анимацию разложения, а кнопка Close закрывает окно и переносит рисунок в текущий документ системы Maple 9 5. 5.13.3. Демонстрация вычисления градиента функции двух переменныхКоманда Gradient… — открывает Maplet-окно демонстрации вычисления градиента функции двух переменных z(x, у) в ряд Тейлора относительно заданной точки (х0, y0). Это окно представлено на рис. 5.34. 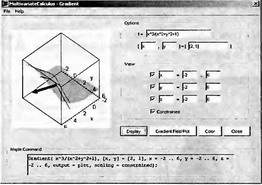 Рис. 5.34. Maplet-окно демонстрации вычисления градиента функции двух переменных Работа с этим окном практически не отличается от описанной для примера с рядом Тейлора. Единственное исключение — новая кнопка Gradient Field Plot. Она позволяет строить график поля градиента с помощью стрелок. Этот случай представлен на рис. 5.35. 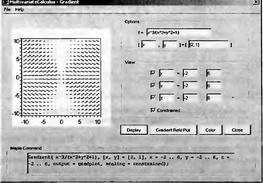 Рис. 5.35. Maplet-окно демонстрации вычисления градиента функции двух переменных с графиком поля градиента 5.13.4. Демонстрация вычисления производной в заданном направленииКоманда Directional Derivatives… — открывает Maplet-окно демонстрации вычисления производных функции двух переменных z(х, у) в заданном направлении, указанном точкой с координатами (х, у). Это окно представлено на рис. 5.36. 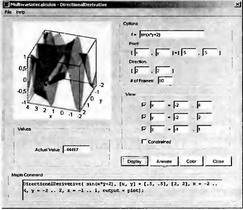 Рис. 5.36. Maplet-окно демонстрации вычисления градиента функции двух переменных Работа с этим окном практически не отличается от описанной для предшествующих примеров. 5.13.5. Демонстрация приближенного вычисления интегралаКоманда Approximate Integration… — открывает Maplet-окно демонстрации вычисления двойных интегралов с подынтегральной функцией двух переменных z(х, у). Это окно представлено на рис. 5.37. 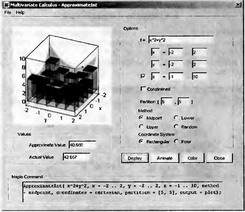 Рис. 5.37. Maplet-окно демонстрации приближенного вычисления двойного интеграла в прямоугольной системе координат Для вычисления интеграла нужно задать подынтегральную функцию и пределы по переменным x и у. Для построения графика можно также задать пределы по переменной z. Приближенное значение интеграла вычисляется суммированием объёмов прямоугольных столбиков, на которые разбивается пространство под поверхностью z(x, у). Число разбиений устанавливается списком Partition. Можно задать один из четырех методов расположения столбиков. В области Value отображается точное и приближенное (сумма объемов столбиков) значения интеграла. Возможно представление интеграла и в полярной системе координат. Пример этого дан на рис. 5.38. 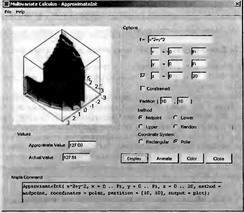 Рис. 5.38. Maplet-окно демонстрации приближенного вычисления двойного интеграла в полярной системе координат 5.13.6. Маплет-демонстрация сечения поверхностиКоманда Cross Section… открывает Maplet-окно демонстрации сечения поверхности плоскостями. Поверхность задается функцией двух переменных z(x, у). Окно этой команды представлено на рис. 5.39. 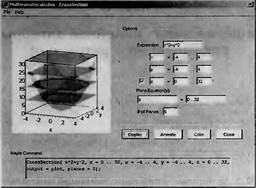 Рис. 5.39. Maplet-окно демонстрации сечения поверхности параллельными плоскостями Работа с этим окном вполне очевидно. На рисунке в левой части окна строится исходная поверхность, секущие плоскости и линии их пересечения. |
|
||
| Главная | В избранное | Наш E-MAIL | Добавить материал | Нашёл ошибку | Наверх | ||||
|
|
||||

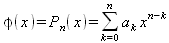 (5.1)
(5.1)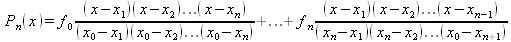 (5.3)
(5.3)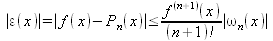 (5.4)
(5.4)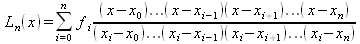 (5.5)
(5.5)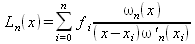 (5.5)
(5.5)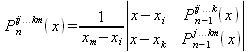 (5.7)
(5.7)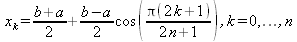 (5.8)
(5.8)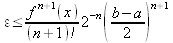 (5.9)
(5.9)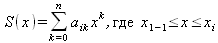 (5.10)
(5.10)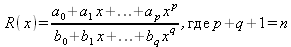 (5.11)
(5.11)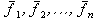 . Будем рассматривать совокупность значений функции f(x) и функции F(x) как координаты двух точек n-мерного пространства. С учетом этого задача приближения функции может быть определена другим образом: найти такую функцию F(x) заданного вида, чтобы расстояние между точками M(f1, f2, …, fn) и
. Будем рассматривать совокупность значений функции f(x) и функции F(x) как координаты двух точек n-мерного пространства. С учетом этого задача приближения функции может быть определена другим образом: найти такую функцию F(x) заданного вида, чтобы расстояние между точками M(f1, f2, …, fn) и 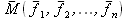 было наименьшим. Воспользовавшись метрикой евклидова пространства, приходим к требованию, чтобы величина
было наименьшим. Воспользовавшись метрикой евклидова пространства, приходим к требованию, чтобы величина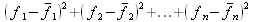 (5.12)
(5.12)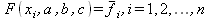 (5.13)
(5.13)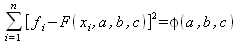 (5.14)
(5.14)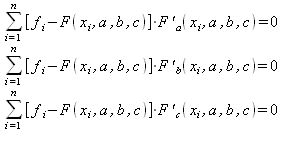 (5.15)
(5.15)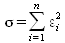 (5.16)
(5.16)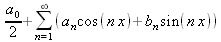 (5.17)
(5.17)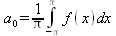 (5.18)
(5.18)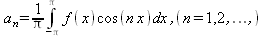 (5.19)
(5.19)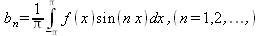 (5.20)
(5.20)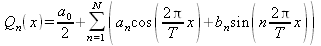 (5.21)
(5.21)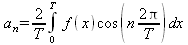 (5.22)
(5.22)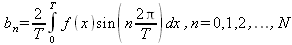 (5.23)
(5.23)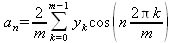 (5.24)
(5.24)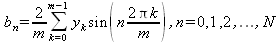 (5.25)
(5.25)