|
||||
|
|
Глава 6Решение задач линейной алгебры, оптимизации и регрессии Задачи линейной алгебры, оптимизации и регрессии — одни из самых массовых в науке, технике и образовании [37, 39–46]. Им и посвящена эта глава. В ней даны основные определения линейной алгебры, основы работы с массивами, векторами и матрицами, функции для работы с векторами и матрицами и для решения систем линейных уравнений. Дано описание средств оптимизации, в том числе новейших системы Maple 10. 6.1. Основные операции линейной алгебры6.1.1. Основные определения линейной алгебрыПрежде чем перейти к рассмотрению обширных возможностей пакетов Maple в решении задач линейной алгебры, рассмотрим краткие определения, относящиеся к ней. Матрица (m×n) — прямоугольная двумерная таблица, содержащая m строк и n столбцов элементов, каждый из которых может быть представлен числом, константой, переменной, символьным или математическим выражением (расширительная трактовка матрицы). Квадратная матрица — матрица, у которой число строк m равно числу столбцов n. Пример квадратной матрицы размера 3×3: 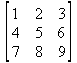 Определитель матрицы — это многочлен от элементов квадратной матрицы, каждый член которого является произведением n элементов, взятых по одному из каждой строки и каждого столбца со знаком произведения, заданным четностью перестановок: 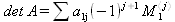 где M1<j>— определитель матрицы порядка n-1, полученной из матрицы А вычеркиванием первой строки и j-го столбца. В таком виде определитель (он же детерминант) легко получить в символьных вычислениях. В численных расчетах мы будем подразумевать под определителем численное значение этого многочлена. Сингулярная (вырожденная) матрица — квадратная матрица, у которой детерминант (определитель) равен 0. Такая матрица обычно не упрощается при символьных вычислениях. Линейные уравнения с почти сингулярными матрицами могут давать большие погрешности при решении. Единичная матрица — это квадратная матрица, у которой диагональные элементы равны 1, а остальные элементы равны 0. Ниже представлена единичная матрица размера 4×4: 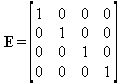 Сингулярные значения матрицы А — квадратные корни из собственных значений матрицы transpose(A)∙А, где transpose(A) — транспонированная матрица А (см. ее определение ниже). Транспонированная матрица — матрица, у которой столбцы и строки меняются местами, то есть элементы транспонированной матрицы удовлетворяют условию AT(i,j)=A(j,i). Приведем простой пример. Исходная матрица: 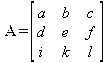 Транспонированная матрица: 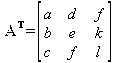 Обратная матрица — это матрица М-1, которая, будучи умноженной на исходную квадратную матрицу М, дает единичную матрицу Е. Ступенчатая форма матрицы соответствует условиям, когда первый ненулевой элемент в каждой строке есть 1 и первый ненулевой элемент каждой строки появляется справа от первого ненулевого элемента в предыдущей строке, то есть все элементы ниже первого ненулевого в строке — нули. Диагональ матрицы — расположенные диагонально элементы Аi,i матрицы А. В приведенной ниже матрице элементы диагонали представлены заглавными буквами: 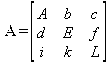 Обычно указанную диагональ называют главной диагональю — для матрицы А, приведенной выше, это диагональ с элементами А, Е и L. Иногда вводят понятия поддиагоналей (элементы d и k) и наддиагоналей (элементы b и f). Матрица, все элементы которой, расположенные кроме как на диагонали, поддиагонали и наддиагонали, равны нулю, называется ленточной. Ранг матрицы — наибольший из порядков отличных от нуля миноров квадратной матрицы. След матрицы — сумма диагональных элементов матрицы. Матрица в целой степени — квадратная матрица в степени n (n — целое неотрицательное число), определяемая следующим образом: М0=Е, М1=М, М2=ММ, …, Мn=Мn-1М. Идемпотентная матрица — матрица, отвечающая условию Р²=Р. Симметрическая матрица — матрица, отвечающая условию Ат=А. Кососимметрическая матрица — матрица, отвечающая условию Ат=-А. Ортогональная матрица — матрица, отвечающая условию Ат=А-1. Нуль-матрица — матрица, все элементы которой равны 0. Блок-матрица — матрица, составленная из меньших по размеру матриц, также можно представить как матрицу, каждый элемент которой — матрица. Частным случаем является блок-диагональная матрица — блок-матрица, элементы-матрицы которой вне диагонали — нуль-матрицы. Комплексно-сопряженная матрица — матрица Ā, полученная из исходной матрицы А заменой ее элементов на комплексно-сопряженные. Эрмитова матрица — матрица А, удовлетворяющая условию Ā=Ат. Собственный вектор квадратной матрицы А — любой вектор х∈Vn, х≠0, удовлетворяющий уравнению Ах=γх, где γ — некоторое число, называемое собственным значением матрицы А. Характеристический многочлен матрицы — определитель разности этой матрицы и единичной матрицы, умноженный на переменную многочлена — |А-γЕ|. Собственные значения матрицы — корни ее характеристического многочлена. Норма — обобщенное понятие абсолютной величины числа. Норма трехмерного вектора ||х|| — его длина. Норма матрицы — значение sup(||Ax||/||x||). 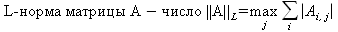 Матричная форма записи системы линейных уравнений — выражение А∙Х=В, где А — матрица коэффициентов системы, X — вектор неизвестных и В — вектор свободных членов. Один из способов решения такой системы очевиден — X=А-1∙В, где А-1 — обратная матрица. 6.1.2. Системы линейных уравнений и их матричная формаКак известно, обычная система линейных уравнений имеет вид: 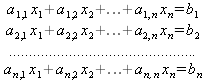 Здесь а1,1, а1,2, …, an,n — коэффициенты, образующие матрицу А и могущие иметь действительные или комплексные значения, х1, х2, …, хn — неизвестные, образующие вектор X и b1, b2, …, bn — свободные члены (действительные или комплексные), образующие вектор В. Эта система может быть представлена в матричном виде как АХ=В, где А — матрица коэффициентов уравнений, X — искомый вектор неизвестных и В — вектор свободных членов. Из такого представления системы линейных уравнений вытекают различные способы ее решения: X=В/А (с применением матричного деления), X=А-1В (с инвертированием матрицы А) и так далее. 6.1.3. Матричные разложенияВ ходе решения задач линейной алгебры часто приходится использовать различные методы, например известный еще из школы метод исключения Гаусса. Однако для эффективного решения таких задач приходится представлять матрицы специальным образом, осуществляя матричные разложения. В ходе этого приходится работать с некоторыми специальными типами матриц, что нередко резко упрощает решения систем линейных уравнений. Отметим некоторые из наиболее распространенных матричных разложений, которые реализованы в большинстве СКА и СКМ. LU-разложение, называемое также треугольным разложением, соответствует матричному выражению вида Р∙А=L∙U, где L — нижняя и U — верхняя треугольные матрицы. Все матрицы в этом выражении квадратные. QR-разложение имеет вид А=Q∙R, где Q — ортогональная матрица, a R — верхняя треугольная матрица. Это разложение часто используется при решении любых систем линейных уравнений, в том числе переопределенных и недоопределенных и с прямоугольной матрицей. Разложение Холецкого А=L∙LT применяется к симметричной матрице А, при этом L — треугольная матрица. Сингулярное разложение матрицы А размера M×N (М×N) определяется выражением А=U∙s∙VT, где U и V — ортогональные матрицы размера N×N и М×M, соответственно, a s — диагональная матрица с сингулярными числами матрицы А на диагонали. 6.1.4. Элементы векторов и матрицЭлементы векторов и матриц в Maple являются индексированными переменными, то есть место каждого элемента вектора определяется его индексом, а у матрицы — двумя индексами. Обычно их обобщенно обозначают как i (номер строки матрицы или порядковый номер элемента вектора) и j (номер столбца матрицы). Допустимы операции вызова нужного элемента и присваивания ему нового значения: V[i] — вызов i-го элемента вектора V; M[i,j] — вызов элемента матрицы М, расположенного на i-й строке в j-м столбце. V[i]:=x — присваивание нового значения х i-му элементу вектора V; M[i,j]:=x — присваивание нового значения х элементу матрицы М. 6.1.5. Преобразование списков в векторы и матрицыПрежде всего, надо обратить внимание на то, что векторы и матрицы, хотя и похожи на списки, но не полностью отождествляются с ними. В этом можно убедиться с помощью следующих примеров (файл vmop), в которых функция type используется для контроля типов множественных объектов (векторов и матриц): > М1:=[1,2,3,4];M1 := [1, 2, 3, 4] > type(M1,vector);false > V:=convert(M1,vector);V := [1, 2, 3, 4] > type(V,vector);true > М2:=[[1,2],[3,4]];М2 := [[1,2], [3, 4]] > type(М2,matrix);false > M:=convert(M2,matrix); 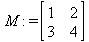 > type(M,matrix);true Таким образом, используя функцию преобразования данных convert, можно преобразовывать одномерные списки в векторы, а двумерные — в матрицы. Функция type используется в следующих формах: type(V,vector) — тестирует аргумент V и возвращает true, если V — вектор, и false в ином случае; type(M.matrix) — тестирует аргумент М и возвращает true, если М — матрица, и false в ином случае. Здесь параметры vector и matrix используются для указания того, какой тип объекта проверяется. Обратите внимание на то, что матрицы отображаются иначе, чем двумерные списки — без двойных квадратных скобок. Отображение вектора подобно отображению одномерного списка, поэтому здесь особенно важен контроль типов данных. 6.1.6. Операции с векторамиВажное достоинство систем компьютерной алгебры, к которым относится и Maple, заключается в возможности выполнения аналитических (символьных) операций над векторами и матрицами. Перед проведением символьных операций с векторами и матрицами рекомендуется очистить память от предшествующих определений с помощью команды restart. Если какие-то элементы векторов или матриц были ранее определены, это может привести к очень сильным искажениям вида конечных результатов. Очистка памяти устраняет возможность ошибок такого рода. Приведем примеры операций над векторами (файл vectop): > V:=array(1..4,[1,2,3,4]);V:= [1, 2, 3, 4] > [V[1], V[2], V[4]];[1, 2, 4] > V[1]:=a: V[3]:=b: > evalm(V);[a, 2, b, 4] > evalm(V+2);[a + 2, 4, b + 2, 6] > evalm(2*V);[2 a, 4, 2 b, 8] > evalm(V**V);[a, 2, b, 4]V > evalm(a*V);[a², 2 a, a b, 4 a] В этих примерах используется функция evalm(M), осуществляющая вычисление матрицы или вектора М. 6.1.7. Операции над матрицами с численными элементамиНад матрицами с численными элементами в Maple можно выполнять разнообразные операции. Ниже приведены основные из них: > М:=array(1..2,1..2,[[1,2],[3,4]]); 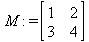 > evalm(2*М); 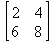 > evalm(2+М); 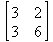 > evalm(M^2); 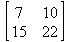 > evalm(М^(-1)); 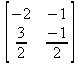 > evalm(М-М);0 > evalm(М+М); 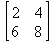 > evalm(М*М); 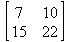 > evalm(M/M);1 > evalm(M^0);1 Рекомендуется внимательно изучить эти примеры и попробовать свои силы в реализации простых матричных операций. 6.1.8. Символьные операции с матрицамиОдной из привлекательных возможностей СКА является возможность проведения символьных операций с матрицами. Ниже представлены примеры символьных операций, осуществляемых над квадратными матрицами одного размера в системе Maple: > M1:=array(1..2,1..2, [[a1,b1], [c1,d1]]); 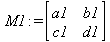 > M2:=array(1..2,1..2,[[a2,b2],[c2,d2]]); 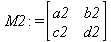 > evalm(M1+M2) 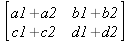 > evalm(M1-M2) 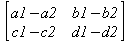 > evalm(Ml&*M2); 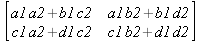 > evalm(M1/М2); 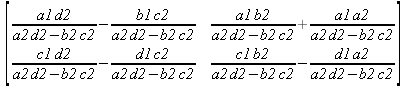 > evalm(M1&/М2); 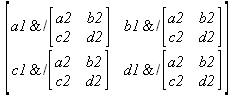 Приведем еще ряд гримеров выполнения символьных операций с одной матрицей: > evalm(M1^2); 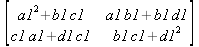 > evalm(sin(M1)); 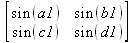 > evalm(M1*z); 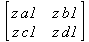 > evalm(M1/z); 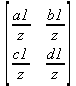 > evalm(M1+z); 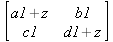 > evalm(M1-z); 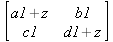 Среди других функций для работы с матрицами полезно обратить внимание на функцию map, которая применяет заданную операцию (например, функции дифференцирования diff и интегрирования int) к каждому элементу матрицы. Примеры такого рода даны ниже: > M:=array(1..2,1..2,[[х,х^2],[х^3,х^4]]); 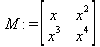 > map(diff,M, x); 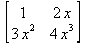 > map(int, %, x); 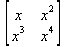 > map(sin, M); 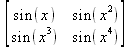 В результате возвращаются матрицы, каждый элемент которых представлен производной или интегралом. Аналогично можно выполнять над матрицами и другие достаточно сложные преобразования. В дальнейшем мы продолжим изучение матричных функций и операций, включенных в пакеты Maple. 6.2. Пакет линейной алгебры linalg системы6.2.1. Состав пакета linalgНесомненно, что уникальной возможностью системы Maple, как и других систем компьютерной алгебры, является возможность решения задач линейной алгебры в символьном (формульном, аналитическом) виде. Однако такое решение представляет скорее теоретический, чем практический интерес, поскольку даже при небольших размерах матриц (уже при 4–5 строках и столбцах) символьные результаты оказываются очень громоздкими и трудно обозримыми. Они полезны только при решении специфических аналитических задач, например с разреженными матрицами, у которых большинство элементов имеют нулевые значения. Поэтому разработчики Maple были вынуждены реализовать в своей системе численные методы решения задач линейной алгебры, которые широко используются в основных сферах ее приложения — математическом моделировании систем и устройств, расчетах в электротехнике, механике, астрономии и т.д. Решение задач линейной алгебры в численном виде можно рассматривать как одну из форм визуализации результатов вычислений, относящихся к линейной алгебре. В ядро Maple, как отмечалось, введены очень скромные и минимально необходимые средства для решения задач линейной алгебры. Основной упор в их реализации сделан на подключаемые пакеты. Основным из них, унаследованным от предшествующих реализаций системы, является пакет решения задач линейной алгебры linalg. Это один из самых обширных и мощных пакетов в области решения задач линейной алгебры. Для их просмотра достаточно использовать команду: > with(linalg); Для большинства пользователей системой Maple набор функций пакета оказывается чрезмерно обширным и потому опущен. Укажем, однако, наиболее употребительные функции пакета linalg: • addcol — добавляет к одному из столбцов другой столбец, умноженный на некоторое число; • addrow — добавляет к одной из строк другую строку, умноженную на некоторое число; • angle — вычисляет угол между векторами; • augment — объединяет две или больше матриц по горизонтали; • backsub — реализует метод обратной подстановки при решении системы линейных уравнений (см. также forwardsub); • band — создает ленточную матрицу; • basis — находит базис векторного пространства; • bezout — создает Bezout-матрицу двух полиномов; • BlockDiagonal — создает блок-диагональную матрицу; • blockmatrix — создает блок-матрицу; • cholesky — декомпозиция Холесского для квадратной положительно определенной матрицы; • charmat — создает характеристическую матрицу (charmat(M,v) матрица, вычисляемая как v∙E-М); • charpoly — возвращает характеристический полином матрицы; • colspace — вычисляет базис пространства столбцов; • colspan — находит базис линейной оболочки столбцов матрицы; • companion — вычисляет сопровождающую матрицу, ассоциированную с полиномом; • cond — вычисляет число обусловленности матрицы (cond(M) есть величина norm(M)∙norm(M-l)); • curl — вычисляет ротор вектора; • definite — тест на положительную (отрицательную) определенность матрицы; • diag — создает блок-диагональную матрицу; • diverge — вычисляет дивергенцию векторной функции; • eigenvals — вычисляет собственные значения матрицы; • eigenvects — вычисляет собственные векторы матрицы; • equal — определяет, являются ли две матрицы равными; • exponential — создает экспоненциальную матрицу; • ffgausselim — свободное от дробей Гауссово исключение в матрице; • fibonacci — матрица Фибоначчи; • forwardsub — реализует метод прямой подстановки при решении системы линейных уравнений (например для матрицы L и вектора b forwardsub(L,b) возвращает вектор решения х системы линейных уравнений L∙x=b); • frobenius — вычисляет форму Фробениуса (Frobenius) матрицы; • gausselim — Гауссово исключение в матрице; • gaussjord — синоним для rref (метод исключения Гаусса-Жордана); • geneqns — генерирует элементы матрицы из уравнений; • genmatrix — генерирует матрицу из коэффициентов уравнений; • grad — градиент векторного выражения; • GramSchmidt — вычисляет ортогональные векторы; • hadamard — вычисляет ограничение на коэффициенты детерминанта; • hessian — вычисляет гессиан-матрицу выражения; • hilbert — создает матрицу Гильберта; • htranspose — находит эрмитову транспонированную матрицу; • ihermite — целочисленная эрмитова нормальная форма; • indexfunc — определяет функцию индексации массива; • innerprod — вычисляет векторное произведение; • intbasis — определяет базис пересечения пространств; • ismith — целочисленная нормальная форма Шмитта; • iszero — проверяет является ли матрица ноль-матрицей; • jacobian — вычисляет якобиан векторной функции; • JordanBlock — возвращает блок-матрицу Жордана; • kernel — находит базис ядра преобразования, соответствующего данной матрице; • laplacian — вычисляет лапласиан; • leastsqrs — решение уравнений по методу наименьших квадратов; • linsolve — решение линейных уравнений; • Ludecomp — осуществляет LU-разложение; • minpoly — вычисляет минимальный полином матрицы; • mulcol — умножает столбец матрицы на заданное выражение; • mulrow — умножает строку матрицы на заданное выражение; • multiply — перемножение матриц или матрицы и вектора; • normalize — нормализация вектора; • orthog — тест на ортогональность матрицы; • permanent — вычисляет перманент матрицы — определитель, вычисляемый без перестановок; • pivot — вращение относительно элементов матрицы; • potential — вычисляет потенциал векторного поля; • Qrdecomp — осуществляет QR-разложение; • randmatrix — генерирует случайные матрицы; • randvector — генерирует случайные векторы; • ratform — вычисляет рациональную каноническую форму; • references — выводит список основополагающих работ по линейной алгебре; • rowspace — вычисляет базис пространства строки; • rowspan — вычисляет векторы охвата для места столбца; • rref — реализует преобразование Гаусса-Жордана матрицы; • scalarmul — умножение матрицы или вектора на заданное выражение; • singval — вычисляет сингулярное значение квадратной матрицы; • singularvals — возвращает список сингулярных значений квадратной матрицы; • smith — вычисляет Шмиттову нормальную форму матрицы; • submatrix — извлекает указанную подматрицу из матрицы; • subvector — извлекает указанный вектор из матрицы; • sumbasis — определяет базис объединения системы векторов; • swapcol — меняет местами два столбца в матрице; • swaprow — меняет местами две строки в матрице; • sylvester — создает матрицу Сильвестра из двух полиномов; • toeplitz — создает матрицу Теплица; • trace — возвращает след матрицы; • vandermonde — создает вандермондову матрицу; • vecpotent — вычисляет векторный потенциал; • vectdim — определяет размерность вектора; • wronskian — вронскиан векторных функций. Назначение многих функция вполне очевидно из названия. Далее мы рассмотрим более подробно некоторые функции из этого пакета. С деталями синтаксиса (достаточно разнообразного) для каждой из указанных функций можно ознакомиться в справочной системе Maple. Для этого достаточно использовать команду ?name;, где name — имя функции (из приведенного списка). 6.2.2. Интерактивный ввод матрицДля интерактивного ввода матриц можно, определив размерность некоторого массива, использовать функцию entermatrix: > с A:=array(1..3,1..3);А := array(1..3, 1..3, []) После исполнения этого фрагмента документа диалог с пользователем имеет следующий вид: > entermatrix(А); enter element 1,1 > 1; enter element 1,2 > 2; enter element 1,3 > 3; enter element 2,1 > 4; enter element 2,2 > 5; enter element 2,3 > 6; enter element 3,1 > 7; enter element 3,2 > 8; enter element 3,3 > 9; 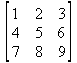 > В:=(%); 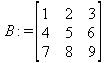 > В[1,1];1 > В[2,2];5 > В[3,3];9 6.2.3. Основные функции для задания векторов и матрицВ библиотечном файле linalg имеются следующие функции для задания векторов и матриц: • vector(n,list) — создание вектора с n элементами, заданными в списке list; • matrix(n,m,list) — создание матрицы с числом строк n и столбцов m с элементами, заданными списком list. Ниже показано применение этих функций (файл linalgop): > V:=vector(3, [12, 34, 56]);V := [12, 34, 56] > M:=matrix(2,3, [1,2,3,4]); 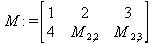 > V[2];34 > М[1, 3];3 > М[2, 3];M2,3 Обратите внимание на последние примеры — они показывают вызов индексированных переменных вектора и матрицы. 6.2.4. Работа с векторами и матрицамиДля работы с векторами и матрицами Maple имеет множество функций, входящих в пакет linalg. Ограничимся приведением краткого описания наиболее распространенных функций этой категории. Операции со структурой отдельного вектора V и матрицы М: • coldim(M) — возвращает число столбцов матрицы М; • rowdim(M) — возвращает число строк матрицы М; • vectdim(V) — возвращает размер вектора V; • col(M.i) — возвращает i-й столбец матрицы М; • row(M,i) — возвращает i-ю строку матрицы М; • minor(M,i,j) — возвращает минор матрицы М для элемента с индексами i и j; • delcols(M,i..j) — удаляет столбцы матрицы М от i-го до j-го; • delrows(V,i..j) — удаляет строки матрицы М от i-й до j-й; • extend(M,m,n,x) — расширяет матрицу М на m строк и n столбцов с применением заполнителя х. Основные векторные и матричные операции: • dotprod(U,V) — возвращает скалярное произведение векторов U и V; • crossprod(U,V) — возвращает векторное произведение векторов U и V; • norm(V) или norm(M) — возвращает норму вектора или матрицы; • copyinto(A,B,i,j) — копирует матрицу А в В для элементов последовательно от i до j; • concat(M1,M2) — возвращает объединенную матрицу с горизонтальным слиянием матриц М1 и М2; • stack(M1,M2) — возвращает объединенную матрицу с вертикальным слиянием М1 и М2; • matadd(A,B) и evalm(A+B) — возвращает сумму матриц А и В; • multiply(A,B) и evalm(A&*B) — возвращает произведение матриц А и В; • adjoint(M) или adj(M) — возвращает присоединенную матрицу, такую, что M∙adj(M) дает диагональную матрицу, определитель которой есть det(M); • charpoly(M,lambda) — возвращает характеристический полином матрицы М относительно заданной переменной lambda; • det(M) — возвращает детерминант (определитель) матрицы М; • Eigenvals(M,vector) — инертная форма функции, возвращающей собственные значения матрицы М и (при указании необязательного параметра vector) соответствующие им собственные векторы; • jordan(M) — возвращает матрицу М в форме Жордана; • hermite(M) — возвращает матрицу М в эрмитовой форме; • trace(M) — возвращает след матрицы М; • rank(M) — возвращает ранг матрицы М; • transpose(M) — возвращает транспонированную матрицу М; • inverse(M) или evalm(1/M) — возвращает матрицу, обратную к М; • singularvals(A) — возвращает сингулярные значения массива или матрицы А. Приведем примеры применения некоторых из этих функций (файл linalgop): > M:=matrix(2,2, [a,b,с,d]); 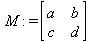 > transpose(M); 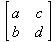 > inverse(M); 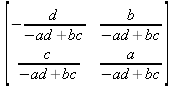 > det(M);ad - bc > rank(M);2 > trace(M);a + d > M:=matrix(2,2,[1,2,3,4]); 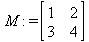 > ev:=evalf(Eigenvals(M,V));ev := [-.372281323, 5.372281323] > eval(V); 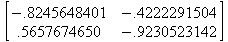 > charpoly(M,p);p² - 5p - 2 > jordan(M); 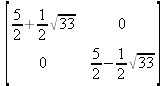 > A:= array([[1,0,1],[1,0,1],[0,1,0]]); 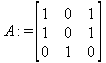 > singularvals(А);[0, 2, 1] В приведенных примерах полезно обратить внимание на то, что многие матричные функции способны выдавать результаты вычислений в аналитическом виде, что облегчает разбор выполняемых ими операций. 6.2.5. Решение систем линейных уравненийОдной из самых распространенных задач линейной алгебры является решение систем линейных уравнений. Ниже представлен простой пример составления и решения трех систем линейных уравнений с применением функций, входящих в пакет linalg (файл sle): > with(linalg): > C:=matrix(3,3,[[4,8,2],[6,2,3],[3,7,11]]); 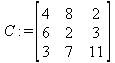 > B:=matrix(3,1, [5,6,1]); 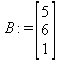 > A:=evalm(C); 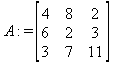 > A1 :=copyinto(В, С, 1, 1); 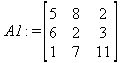 > C:=evalm(A):А2:=copyinto(В,С,1,2); 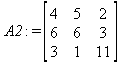 > C:=evalm(A):A3:=copyinto(В,С,1,3); 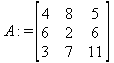 > x1:=det(A1)/det(А); 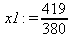 > x2:=det(A2)/det(A); 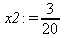 > x3:=det(A3)/det(a); 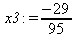 А теперь рассмотрим пример решения матричного уравнения в символьном виде: > A:=matrix(2,2,[a,b,с,d]); 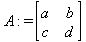 > В:=vector(2, [с,d]);В := [с, d] > X:=linsolve(А,В); 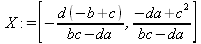 Следующий пример показывает решение более сложной системы линейных уравнений с комплексными коэффициентами: > А:=matrix(2,2,[[10+200*1,-200*1],[-200*1,170*1]]); 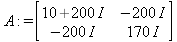 > B:=vector(2, [5,0]);В := [5, 0] > X:=multiply(inverse(А),В); 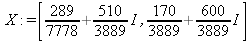 > Digits:=5: convert(eval(X),float);[.037156 + .13114I, .043713 +.15428I] На этот раз решение получено использованием функций умножения матриц и вычисления обратной матрицы в виде X=А-1∙В, то есть в матричном виде. В конце примера показано преобразование результатов с целью их получения в обычной форме комплексных чисел с частями, представленными в форме чисел с плавающей точкой. 6.2.6. Визуализация матрицКак видно из описанного, многие вычисления имеют результаты, представляемые в форме матриц. Иногда такие результаты можно наглядно представить графически, например, в виде гистограммы. Она представляет собой множество столбцов квадратного сечения, расположенных на плоскости, образованной осями строк (row) и столбцов (column) матрицы. При этом высота столбцов определяется содержимым ячеек матрицы. Такое построение обеспечивает графическая функция matnxplot из пакета plots. На рис. 5.1 показано совместное применение этой функции с двумя функциями пакета linafg, формирующими две специальные матрицы А и В. 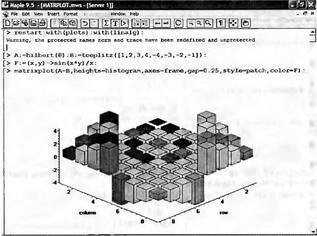 Рис. 6.1. Графическое представление матрицы На рис. 6.1 показана графическая визуализация матрицы, полученной как разность матриц A и В. Для усиления эффекта восприятия применяется функциональная закраска разными цветами. Для задания цвета введена процедура F. 6.3. Работа с пакетом LinearAlgebra и алгоритмами NAG6.3.1. Назначение и загрузка пакета LinearAlgebraВ новых реализациях систем Maple была сделана ставка на использование давно апробированных быстрых алгоритмов линейной алгебры, предложенных создателями Number Algorithm Group (NAG). Эти алгоритмы издавна применяются на больших ЭВМ и суперкомпьютерах, обеспечивая ускорение численных матричных операций от нескольких раз до нескольких десятков раз. Их применение обеспечивает эффективное использование систем символьной математики в решении задач, сводящихся к задачам линейной алгебры. В числе таких задач многочисленные задачи теоретической электротехники, механики многих объектов, моделирования электронных устройств и т.д. В Maple 9.5/10 использование алгоритмов NAG реализуется пакетом LinearAlgebra. Для его загрузки используются следующие команды (файл NAG): > restart; with(LinearAlgebra): > infolevel[LinearAlgebra]:=1;infolevelLinearAlgebra:= 1 Многие функции этого пакета (их большой список опущен) повторяет по назначению функции более старого пакета linalg, описанного выше. Поэтому мы не будем останавливаться на их повторном описании. Главное то, что эти функции задействуют возможности быстрых алгоритмов NAG и, в отличие от функций пакета linalg, ориентированы на численные расчеты в том формате обработки вещественных чисел, который характерен для применяемой компьютерной платформы. Знающий матричные методы читатель легко поймет назначение функций пакета LinearAlgebra по их составным названиям. Например, DeleteColumn означает удаление столбца матрицы, ToeplitzMatrix означает создание матрицы Теплица, ZeroMatrix — создание матрицы с нулевыми элементами и т.д. Все имена функций этого пакета начинаются с заглавной буквы. 6.3.2. Примеры матричных операций с применением пакета LinearAlgebraПрименение алгоритмов NAG особенно эффективно в том случае, когда используется встроенная в современные микропроцессоры арифметика чисел с плавающей запятой. С помощью специального флага такую арифметику можно отключать или включать: > UseHardwareFloats := false; # use software floatsUse Hardware Floats := false > UseHardwareFloats := true; # default behaviourUseHardwareFloats := true Матрицы в новом пакете линейной алгебры могут задаваться в угловых скобках, как показано ниже: > М1:=<<1|2>,<4|5>>; М2:=<<1|2.>, <4|5>>; 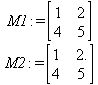 После этого можно выполнять с ними типовые матричные операции. Например, можно инвертировать (обращать) матрицы: > М1^(-1); М2^(-1); 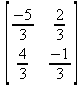 MatrixInverse: "calling external function" MatrixInverse: "NAG" hw_f07adf MatrixInverse: "NAG" hw_f07ajf 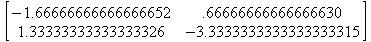 Обратите внимание, что Maple теперь выдает информационные сообщения о новых условиях реализации операции инвертирования матриц с вещественными элементами и, в частности, об использовании алгоритмов NAG и арифметики, встроенной в сопроцессор. Следующий пример иллюстрирует создание двух случайных матриц M1 и М2 и затем их умножение: > M1:=RandomMatrix(2,3); М2:=RandomMatrix(3,3); Multiply(M1,M2,'inplace'); M1; 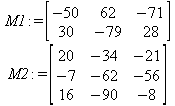 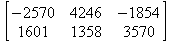 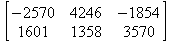 Параметр inplace в функции умножения обеспечивает помещение результата умножения матриц на место исходной матрицы М1 — излюбленный прием создателей быстрых матричных алгоритмов NAG. Поскольку матрицы M1 и М2 заданы как случайные, то при повторении этого примера результаты, естественно, будут иными, чем приведенные. Другой пример иллюстрирует проведение хорошо известной операции LU-разложения над матрицей М, созданной функцией Matrix: > M:=Matrix([[14,-8,1],[-11,-4,18],[3,12,19]], datatype=float); LUDecomposition(М,output=['NAG'],inplace); ipiv:=%[1]; M; 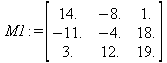 LUDecomposition: "calling external function" LUDecomposition: "NAG" hw_f07adf 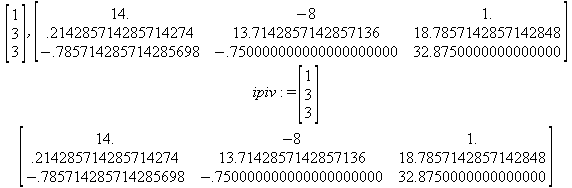 6.3.3. Методы решения систем линейных уравнений средствами пакета LinearAlgebraКонечной целью большинства матричных операций является решение систем линейных уравнений. Для этого пакет LinearAlgebra предлагает ряд методов и средств их реализации. Основными методами решения являются следующие: • обращением матрицы коэффициентов уравнений и решением вида Х=А-1*В; • применением метода LU-декомпозиции (method='LU'); • применением метода QR-декомпозиции (method='QР'); • применением метода декомпозиция Холесского (method='Cholesky'); • метод обратной подстановки (method='subs'). Решение с применением обращения матрицы коэффициентов левой части системы уравнений А уже не раз рассматривалось и вполне очевидно. В связи с этим отметим особенности решения систем линейных уравнений другими методами. Любопытно отметить, что указание метода может быть сделано и без его заключения в одинарные кавычки. 6.3.4. Решение системы линейных уравнений методом LU-декомпозицииЗададим матрицу А левой части системы уравнений и вектор свободных членов В: > restart; with(LinearAlgebra): UseHardwareFloats := false: > A:=<<4|.24|-.08>,<.09|3|-.15>,<.041-.08|4>>; B:=<8, 9, 20>; 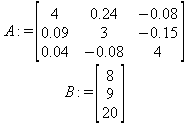 Прямое решение этим методом выполняется одной из двух команд, отличающихся формой записи: > х := LinearSolve(А, В, method= 'LU'); х := LinearSolve(<А|B>, method='LU'); 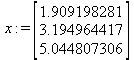 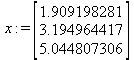 Проверим решение данной системы уравнений: > А.х-В; 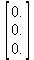 В данном случае решение точно (в пределах точности вычислений по умолчанию). Можно также выполнить решение проведя отдельно LU-декомпозицию, что делает наглядным алгоритм решения и операции подстановки: > P,L,U:=LUDecomposition(A); 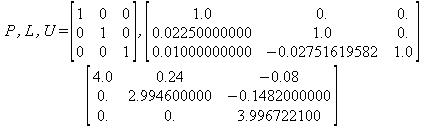 > V2:=Transpose(Р).В; 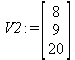 > V3:=ForwardSubstitute(L,V2); 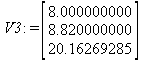 > x:=BackwardSubstitute(U,V3); 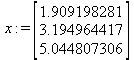 > A.x-B;  6.3.5. Решение системы линейных уравнений методом QR-декомпозицииВыполним теперь решение для тех же исходных данных методом QR-декомпозиции, обозначив метод в функции LinearSolve: > х := LinearSolve(А, В, method='QR'); 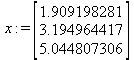 > A.x-B;  Другой, более явный, но и более громоздкий метод решения представлен ниже: > Q,R := QRDecomposition(А);  > V2:=Transpose(Q).B; 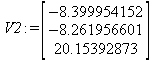 > x:=BackwardSubstitute(R,V2); 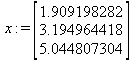 > A.x-B; 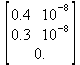 Тут, пожалуй, любопытно, что погрешность вычислений оказалась несколько выше, чем при использовании функции LinearSolve. Однако погрешность не выходит за рамки допустимой по умолчанию. 6.3.6. Решение системы линейных уравнений методом декомпозиции ХолесскиВыполним решение еще и методом декомпозиции Холесски: > x:=LinearSolve(А, В, method='Cholesky'); 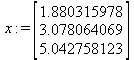 Приведем еще один пример решения системы из четырех линейных уравнений с применением метода декомпозиции Холесски: > M_temp := Matrix(4, (i,j)->i+i*j-7, shape=triangular[lower]); M :=M_temp.Transpose(M_temp); IsMatrixShape(M, symmetric); IsDefinite(M); 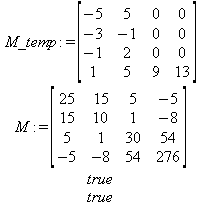 > V := <6,1,3,-2>; 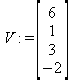 > x:=LinearSolve(M, V, method='Cholesky'); 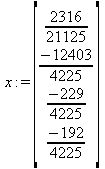 > M.x-V; 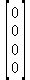 > M:=Matrix(3, (i,j)->i+2*j-8, shape=triangular[lower]); V:=<7,8,1>; 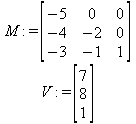 > x := ForwardSubstitute(M, V); x := LinearSolve(M, V); 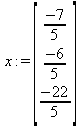 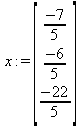 6.3.7. Одновременное решение нескольких систем уравненийМы ограничимся простым примером одновременного решения сразу трех систем уравнений. Дабы не загромождать книгу массивными выражениями, ограничимся решением систем из двух линейных уравнений, матрица коэффициентов у которых одна, а векторы свободных членов разные. Ниже показан пример решения такой системы: > М:=Matrix([[1.,3],[4,5]],datatype=float); V1:=<1.,2>; V2:=<7,-11>; V3:=<-34,-67>; 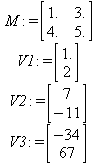 > LinearSolve(М,<V1|V2|V3>); 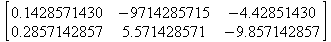 > М: =Matrix([[1.,3],[4,5]],datatype=float); ipiv, M := LUDecomposition(M,output=['NAG'], inplace); LinearSolve([ipiv, M], <V1|V2|V3>); 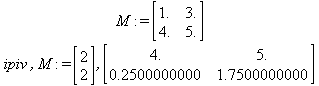 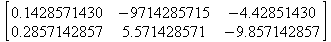 Ha этом мы завершаем обзор пакета LinearAlgebra. Читатель, познающий или знающий методы линейной алгебры, может опробовать в работе любые функции этого пакета самостоятельно или познакомиться с множеством примеров, размещенных в справочной системе Maple и в файле демонстрационных примеров LE_Linear_Solve.mws. Возможности пакетов linalg и LinearAlgebra удовлетворят самых требовательных специалистов в этой области математики. 6.4. Интеграция Maple с MATLAB6.4.1. Краткие сведения о MATLABНесмотря на обширные средства линейной алгебры (да и многие другие), имеющиеся у системы Maple, есть системы компьютерной математики, решающие некоторые классы задач более эффективно, и прежде всего быстрее. В области линейной алгебры к таким системам, безусловно, относится система MATLAB [10, 28–34), созданная компанией MathWorks, Inc. Ее название происходит именно от слов MATrix LABoratory — матричная лаборатория. MATLAB содержит в своем ядре многие сотни матричных функций и является одной из лучших матричных систем для персональных компьютеров. Она реализует самые современные алгоритмы матричных операций, включая, кстати, и алгоритмы NAG. Однако главное достоинство MATLAB — наличие множества дополнительных пакетов как по классическим разделам математики, так и по самым новейшим, таким как нечеткая логика, нейронные сети, идентификация систем, обработка сигналов и др. Знаменитым стал пакет моделирования систем и устройств Simulink, включаемый в пакет поставки системы MATLAB. Последней версией системы является MATLAB 7 SP2. В то же время нельзя не отметить, что MATLAB — одна из самых громоздких математических систем. Инсталляция ее полной версии занимает около 2 Гбайт дискового пространства. Несмотря на это, интеграция различных математических систем с данной системой, похоже, становится своеобразной модой. Такая возможность предусмотрена и в системе Maple с помощью пакета Matlab. 6.4.2. Загрузка пакета расширения MatlabДля загрузки пакета Matlab используется команда > with(Matlab);[chol, closelink, defined, det, dimensions, eig, evalM, fft, getvar, inv, lu, ode45, openlink, qr, setvar, size, square, transpose ] Использование этой команды ведет к автоматическому запуску системы MATLAB и установлению необходимой объектной связи между системами Maple и MATLAB — рис. 6.2. Обратите внимание на то, что такая связь установлена для последней реализации MATLAB 7.04.365 SP2.  Рис. 6.2. Установление связи между системами Maple и MATLAB Как нетрудно заметить, данный пакет дает доступ всего к 18 функциям системы MATLAB (из многих сотен, имеющихся только в ядре последней системы). Таким образом, есть все основания полагать, что возможности MATLAB в интеграции с системой Maple используются пока очень слабо и носят рудиментарный характер. Стоит ли ради этих функций иметь на компьютере огромную систему MATLAB, пользователи должны решать сами. Если ответ положительный, то, скорее всего, пользователь решает тот класс задач, для которых лучше подходит MATLAB и надо задуматься уже над тем, нужна ли в этом случае СКМ Maple. 6.4.3. Типовые матричные операции пакета расширения MatlabБольшинство функций пакета Matlab (не путайте с системой MATLAB, имя которой надо записывать прописными буквами) реализуют самые обычные матричные операции, что и иллюстрируют приведенные ниже примеры (файл matlabi). Зададим матрицу М в формате Maple: > maplematrix_a:=array(1..3,1.-3, [[6,4,2], [7,8,1], [3,7,3]]); 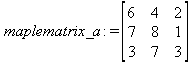 Ниже даны примеры транспонирования матрицы, ее инвертирования, вычисления детерминанта и собственных значений матрицы: > Matlab[transpose](maplematrix_а); 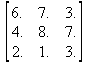 > Matlab[inv](maplematrix_a); 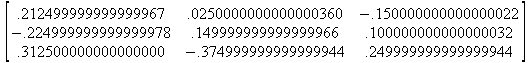 > Matlab[det](maplematrix_a);80. > Matlab[eig](maplematrix_a); 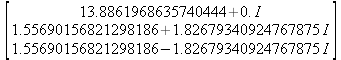 Можно проверить, является ли матрица квадратной: > Matlab[square](maplematrix_a);true а также вычислить размер матрицы: > Matlab[dimensions](maplematrix_a);[3,3] Можно также проверить, является ли данная матрица матрицей системы MATLAB: > Matlab[defined]("maplematrix_a");false Здесь надо иметь в виду, что форматы матриц в системах Maple и MATLAB различны. Выполним LU-преобразование матрицы: > Matlab[lu](maplematrix_a,output='L'); 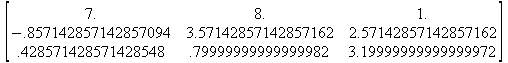 Таким образом, видно, что Maple в данном случае реализует типовые матричные операции, но средствами системы MATLAB. Загрузка последней происходит автоматически при загрузке пакета MATLAB. Если система MATLAB не установлена на вашем компьютере, то доступ к функциям пакета Matlab будет отсутствовать, a Maple при попытке использования данных функций будет выдавать сообщения об ошибках. 6.5. Линейная оптимизация и линейное программирование6.5.1. Постановка задачи линейного программированияВ общем случае задача линейного программирования может быть сформулирована следующим образом: найти максимум или минимум целевой функции 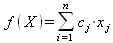 при ограничениях 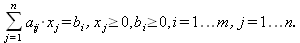 Для решения задач линейного программирования разработано большое количество различных методов. При анализе моделей с двумя или тремя переменными часто используются графические построения на плоскости или в пространстве. Среди универсальных методов решения наиболее распространен симплексный метод. Симплекс — это многоугольник, перемещаемый в пространстве решения таким образом, чтобы постепенно сужаясь он мог охватить точку искомого решения, отвечающую решению задачи с заданной погрешностью. При этом методе задается некоторое начальное приближение, удовлетворяющее всем ограничениям задачи, но не обязательно оптимальное. Оптимальность результата достигается последовательным улучшением исходного варианта за определенное число шагов (итераций). Направление перехода от одной итерации к другой выбирается на основе критерия оптимальности целевой функции задачи. Реализовывать симплекс-метод вручную — громоздко и сложно. Системы компьютерной математики имеют средства решения задач оптимизации, в том числе и симплекс-методом. Рассмотрим примеры решения несколько типичных задач линейного программирования с помощью таких средств системы Maple 9.5. 6.5.2. Обзор средств пакета simplexВ пакете simplex системы Maple имеется небольшой, но достаточно представительный набор функций и определений для решения задач линейной оптимизации и программирования: > with(simplex); Warning, the protected names maximize and minimize have been redefined and unprotected[basis, convexhull, cterm, define_zero, display, duial, feasible, maximize, minimize, pivot, pivoteqn, pivotvar, ratio, setup, standardize] Приведем краткое назначение этих функций: • basis возврат списка основных переменных для множества линейных уравнений; • convexhull — вычисление выпуклой оболочки для набора точек; • cterm — задание констант для системы уравнений или неравенств; • define_zero — определение наименьшего значения, принимаемого за ноль (по умолчанию увязано со значением системной переменной Digits); • display — вывод системы уравнений или неравенств в матричной форме; • dual — выдача сопряженных выражений; • equality — параметр для функции convert, указывающая на эквивалентность; • feasible — выяснение возможности решения заданной задачи: • maximize — вычисление максимума функции; • minimize — вычисление минимума функции; • pivot — создание новой системы уравнений с заданным главным элементом; • pivoteqn — выдача подсистемы уравнений для заданного главного элемента; • pivotvar — выдача переменных с положительными коэффициентами в целевой функции; • ratio — выдача отношений для определения наиболее жесткого ограничения; • setup — задание системы линейных уравнений; • standardize — приведение заданной системы уравнений или неравенств к стандартной форме неравенств типа «меньше или равно». 6.5.3. Переопределенные функции maximize и minimizeГлавными из этих функций являются maximize и minimize, оптимизирующие задачу симплекс-методом. Они записываются в следующих формах: maximize(f, С) minimize(f, С) minimize(f , С, vartype) maximize(f , C, vartype) maximize(f , C, vartype, 'NewC', 'transform') minimize(f , C, vartype, 'NewC', 'transform') Здесь f — линейное выражение, С — множество или список условий, vartype — необязательно задаваемый тип переменных NONNEGATIVE или UNRESTRICTED, NewC и transform — имена переменных, которым присваиваются соответственно оптимальное описание и переменные преобразования. Ниже даны примеры применения этих функций (файл simplex): > restart:with(simplex): Warning, the protected names maximize and minimize have been redefined and unprotected > minimize(x+y, {4*x+3*y <= 5, 3*x+4*y <= 4}, NONNEGATIVE);{y=0, x=0} > minimize(x-y, {4*x+2*y <= 10, 3*x+4*y <= 16}, NONNEGATIVE, 'NC', 'vt');{y=4, x=0} > NC;vt; 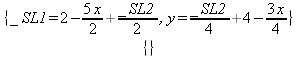 > maximize(x+y, {4*x+2*y <= 10, 3*x+4*y <= 16}, NONNEGATIVE); 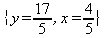 > maximize(x+y, {3*x+2*y <= 5, 2*x+4*y <=4}); 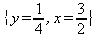 > z := 2*x1 - x2 + 3*x3;z := 2x1 - x2 + 3x3 > cnts1 := [x2+2*x3 <= 1, 2*x1-4*x2+6*x3 <= 3, -x1+3*x2+4*x3 <= 12];cnts1 := [x2+2x3 ≤ 1, 2x1-4x2+6x3 ≤ 3, -x1+3x2+4x3 ≤ 12] > sol1 := maximize(z,cnts1,NONNEGATIVE); 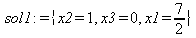 При использовании функций minimize и maximize надо не забывать, что это переопределенные функции — аналогичные по названию функции есть в ядре и они реализуют иные методы вычислений. Для возврата к исходному определению функций надо выполнить команду restart. 6.5.4. Прочие функции пакета simplexФункция basis(C) возвращает базис для системы линейных уравнений С. Например: > basis([х = 2*z+w, z = 2*y-w]);[x, z] Функция convexhull(ps) возвращает выпуклую оболочку множества точек ps. Например: > convexhull({[0,0], [1,1], [2,-1], [1,1/3],[1,1/2]));[[0, 0], [2, -1], [1, 1]] Для определения констант для системы линейных уравнений или неравенств служит функция cterm(C): > cterm([2*х+y<=6,7*y-z-3=4]);[6, 7] Функция define zero(C) возвращает ближайшее ненулевое значение, зависящее от установки переменной Digits: > define_zero();.1000000000 10-7 > Digits:=40;Digits := 40 > define_zero();.1000000000000000000000000000000000000000 10-37 > define_zero(1*10^(-10));.1000000000000000000000000000000000000000 10-9 Функция display(C) имеет еще и форму display(C,[x, у, z]). Она задает вывод линейных уравнений и неравенств в матричной форме: > display({2*x+5*y-z<= 0, 2*w-4*y-z<=2}); 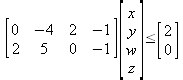 Функция dual(f, С, у) имеет следующие параметры: f — линейное выражение, С — множество неравенств и у — имя. Эта функция возвращает сопряженное с f выражение: > dual(х-y,{2*х+3*y<=5,3*х+6*y<=15}, z);15z1+5z2, {1 ≤ 3z1+2z2, -1 ≤ 6z1+3z2} Функция feasible может быть задана в трех формах: feasible(С) feasible(С,vartype) feasible(С,vartype,'NewC','Transform') Здесь параметр vartype может иметь значения NONNEGATIVE или UNRESTRICTED. Эта функция определяет систему как осуществимую или нет: > feasible({2*х+3*y<=5, 3*х+6*y<=15), NONNEGATIVE);true > feasible({2*х+3*y<=5, 3*х+6*y<=-15}, NONNEGATIVE);false Если функция возвращает логическое значение true, то заданная система осуществима, а если false — неосуществима, то есть ни при каких значениях переменных не способна удовлетворить записанным неравенствам и равенствам. Функция pivot(C, х, eqn) конструирует новую систему с заданным главным элементом: > pivot({_SL1=5-4*x-3*y,_SL2=4-3*x-4*y),х,[_SL1=5-4*x-3*y]); 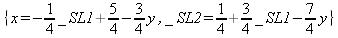 Функция pivoteqn(C, var) возвращает подсистему для заданного диагонального элемента С: > pivoteqn((_SL1 = 5-3*х-2*y, _SL2 = 4-2*х-2*y}, х);[_SL1 = 5 - 3х - 2y] Функция pivotvar(f, List) или pivotvar(f) возвращает список переменных, имеющих положительные коэффициенты в выражении для целевой функции: > pivotvar(x1-2*x2+3*x3-x4);x1 > pivotvar(x1+2*х3-3*х4, [x4,x3,x1]);x3 Функция ratio(C, х) возвращает список отношений, задающих наиболее жесткие ограничения: > ratio([SL1=10-3*x-2*y, SL2=8-2*x-4*y], x); 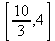 Функция setup может иметь три формы: setup(С) setup(С, NONNEGATIVE) setup(С, NONNEGATIVE, 't') Она обеспечивает конструирование множества уравнений с переменными в левой части: > setup({2*х+3*y<=5,3*х+5*y=15)); 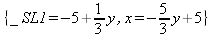 Последняя функция — standartize(C) — конвертирует список уравнений (неравенств) в неравенства типа «меньше или равно»: > standardize({2*х+3*у<=5,3*х+5*у=15});{2 х + 3 y ≤ 5, 3х + 5у ≤ 15, -3х -5y ≤ -15} 6.6. Новый пакет оптимизации Optimization в Maple 9.5В систему Maple 9.5 был добавлен новый пакет оптимизации Optimization, основанный на новейших существенно улучшенных алгоритмах оптимизации. С его помощью можно решать не только задачи линейного, но и квадратичного и нелинейного программирований с повышенной степенью визуализации. 6.6.1. Доступ к пакету Optimization и его назначениеПакет оптимизации Optimization вызывается как обычно: > with(Optimization);[ImportМPS, Interactive, LPSolve, LSSolve, Maximize, Minimize, NLPSolve, QPSolve] Warning, the name changecoords has been redefined Для получения справки по пакету надо исполнить команду: > help(Optimization); Пакет использует при вычислениях алгоритмы группы NAG, которые считаются наиболее эффективными при реализации численных методов вычислений, в частности реализующих алгоритмы оптимизации. Пакет вводит 8 функций. Две из них это переопределенные функции вычисления максимума Maximize и минимума Minimize. Кроме того, пакет имеет 4 решателя уравнений с заданными ограничениями, реализующих следующие методы: • LPSolve — линейное программирование; • LSSolve — улучшенная реализация метода наименьших квадратов; • QPSolve — квадратичное программирование; • NLPSolve — нелинейное программирование. Функция ImportMPC обеспечивает ввод данных для оптимизации из файла, а функций Interactive позволяет работать с интерактивным Maplet-окном для оптимизации. С пакетом Optimization можно познакомиться по его справке. В ее разделе Examples есть довольно обширный документ с примерами применения пакета — дополнительными к тем, которые даются к функциям пакета в справке. Начало этого документа представлено на рис. 6.3. В нем представлены основные задачи, решаемые пакетом Optimization — линейное, квадратичное и нелинейное программирование, а также приближение данных и функциональных зависимостей методом наименьших квадратов (нелинейная регрессия). 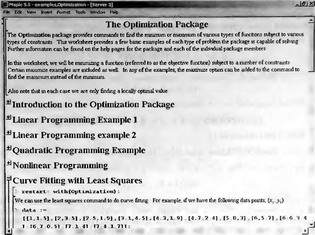 Рис. 6.3. Начало документа с примерами применения пакета Optimization 6.6.2. Работа с функциями Minimize и MaximizeФункции Minimize и Maximize служат для поиска минимумов и максимумов математических выражений с учетом ограничений самыми современными численными методами. Функции записываются в виде: Minimize(obj [, constr, bd, opts]) Minimize(opfobj [, ineqcon, eqcon, opfbd, opts]) Maximize(obj [, constr, bd, opts]) Maximize(opfobj [, ineqcon, eqcon, opfbd, opts]) Параметры функций следующие: • obj — алгебраический объект, целевая функция; • constr — список с ограничивающими условиями; • bd — последовательность вида name=range, задающая границы для одной или более переменных; • opts — равенство или равенства вида option=value, где option одна из опции feasibilitytolerance, infinitebound, initialpoint, iterationlimit или optimalitytolerance, специфицированных в команде Minimize или Maximize. • opfobj — процедура, целевая функция; • ineqcon — множество или список процедур с ограничениями типа неравенств; • eqcon — множество или список процедур с ограничениями типа равенств; • opfbd — последовательность пределов; границы для всех переменных; Примеры применения этих функций представлены ниже: > Maximize(sin(х)/х);[1., [х=2.93847411867272567 10-11]] > Minimize(х^2+у^2);[0., [х=0., у=0.]] > Minimize(sin(х)/х, initialpoint={x=5});[-0.217233628211221636 , [х=4.49340945792364720 ]] > Maximize(sin(x*y*z));[1., [x=1.16244735150962364, z=1.16244735150962364, y=1.16244735150962364]] > Minimize(2*х+3*y, {3*х-y<=9, х+y>=2}, assume=nonnegative);[4., [х=2., y=0.]] Из этих примеров видно, что результаты вычислений представляются в виде чисел с плавающей точкой с так называемой двойной точностью (правильнее было бы сказать с двойной длиной или разрядностью). При вычислениях используются алгоритмы группы NAG и решатели, описанные ниже. 6.6.3. Линейное программирование — LPSolveДля решения задач линейного программирования в пакете Optimization введена функция: LPSolve(obj [, constr, bd, opts]) Она имеет следующие параметры: • obj — алгебраическое выражений, целевая функция; • constr — множество или список линейных ограничений; • bd — последовательность вида name=range, задающая границы одной или многих переменных; • opts — равенство или равенства в форме option=value, где option одна из опций assume, feasibilitytolerance, infinitebound, initialpoint, iterationlimit или maximize, специализированных для команды LPSolve. Пример на решение задачи линейного программирования дан на рис. 6.4. Здесь оптимизируется целевая функция -3x-2у, которая линейно зависит от переменных х и у. В этом примере интересна техника графической визуализации решения.  Рис. 6.4. Пример решения задачи линейного программирования Эта функция может задаваться также в матричной форме: LPSolve(c [, lc, bd, opts]) Здесь с вектор, задающий целевую функция, остальные параметры были определены выше. Пример применения функции LPSolve в матричном виде представлен ниже: > с := Vector([-1,4,-2], datatype=float): bl := Vector([2,3,1], datatype=float): bu := Vector([5,8,2.5], datatype=float): LPSolve(с, [], [bl, bu]); ┌ ┌ ┐┐ │ │ 5. ││ │ │ ││ │2.,│ 3. ││ │ │ ││ │ │ ││ └ └2.50000000000000000┘┘ Ряд других подобных примеров применения функции LPSolve можно найти в справке по этой функции. 6.6.4. Квадратичное программирование — QPSolveДля реализации квадратичного программирования служит функция QPSolve(obj, constr, bd, opts) С параметрами, описанными выше для функции LPSolve. Пример реализации квадратичного программирования представлен на рис. 6.5. Здесь оптимизируется выражение -3х²-2y², которое квадратично зависит от переменных x и у. Здесь также интересна техника визуализации квадратичного программирования.  Рис. 6.5. Пример квадратичного программирования Эта функция также может быть записана в матричной форме: QPSolve(obj, lc, bd, opts) Пример применения этой функции дан ниже: > с := Vector([2, 5.1 , datatype=float): H := Matrix([[6, 3], [3, 4]], datatype=float): A := Matrix([[-1,1]], datatype=float): b := Vector([-2], datatype=float): QPSolve([с, H], [A, b]); ┌ ┌0.46666666666666564┐┐ │-3.5333333333333,│ ││ │ │-1.6000000000000030││ └ └ ┘┘ Ряд подобных примеров можно найти в справке по данной функции. 6.6.5. Нелинейное программирование — NLPSolveНелинейное программирование позволяет решать задачи оптимизации при нелинейных зависимостях целевой функции от ее аргументов. Для этого в пакете Optimization имеется функция: NLPSolve(obj, constr, bd, opts) NLPSolve(opfobj, ineqcon, eqcon, opfbd, opts) Ее параметры те же, что и у ранее описанных функций. В связи с этим ограничимся парой примеров ее применения при целевых функциях одной и двух переменных: > NLESolve(х*ехр(-х), х=0..6, maximize);[0.367879441171442278, [х=0.99999998943752966]] > NLPSolve(х*y*ехр(-х)*ехр(-y), х=0..6, y=0..6,maximize);[0.135335283236612674, [х=0.99999999994630706, y=1.00000000003513966]] В оптимизируемых функциях этих примеров присутствует экспоненциальная зависимость, что и указывает на решение задачи нелинейного программирования. Однако следует отметить, что ограничения должны быть линейными — в противном случае возвращается сообщение об ошибке с указанием на необходимость обеспечения линейности ограничивающих условий. Возможна и матричная форма функции: NLPSolve(n, р, nc, nlc, lc, bd, opts) NLPSolve(n, р, lc, bd, opts) Примеры на ее применение можно найти в справке по функции NLPSolve. 6.6.6. Работа с функцией импорта данных из файлов — ImportMPCДля импорта данных из файлов служит функция: ImportMPS(filename [, maxm, maxn, lowbnd, upbnd, opts]) В ней используются следующие параметры: • filename — имя файла для MPS(X) в виде строки; • maxm — максимальное число линейных ограничений; • maxn — максимальное число переменных; • lowbnd — значение нижней границы для переменных; • upbnd — значение верхней границы для переменных; • opts — выражения в виде опций, записываемых в форме option=value, где option один из объектов rhsname, rangename или boundsname, заданный для Import MPS команд. С деталями применения этой функции можно ознакомиться по справке по ней. 6.6.7. Нелинейная регрессияНаконец в Maple 9.5 появились средства для полноценной нелинейной регрессии (реализации метод наименьших квадратов для произвольных приближающих зависимостей). Для этого служит функция: LSSolve(obj, constr, bd, opts) LSSolve(opfobj, ineqcon, eqcon, opfbd, opts) Большинство ее параметров уже описывалось. Исключением является параметр opfobj — список процедур для остатков (разностей) метода наименьших квадратов. Пример применения этой функции для приближения облака заданных точек data нелинейной зависимостью с именем р дан на рис. 6.6. 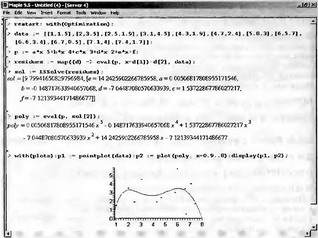 Рис. 6.6. Пример нелинейной регрессии с помощью функции LSSolve 6.6.8. Маплет-оптимизация с помощью функции InteractiveФункция Interactive служит для организации интерактивной оптимизации в Maplet-окне. Эта функция может задаваться в виде: Interactive() Interactive(obj, constr) В первом случае открывается «пустое» Maplet-окно, а во втором окно с введенной целевой функцией obj и ограничивающими условиями constr. Вид окна с примером квадратичной оптимизации представлен на рис. 6.7. 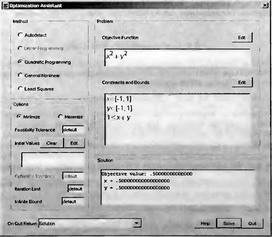 Рис. 6.7. Пример квадратичной оптимизации в Maplet-окне В левом верхнем углу окна имеется список классов задач оптимизации. Справа расположены панели для ввода оптимизируемого выражения и ограничивающих условий. Кнопки Edit позволяют вызывать простые окна для редактирования их, а кнопка Solve запускает вычисления, результат которых появляется в окошке Solution. Остальные элементы интерфейса Maplet-окна в особых пояснениях не нуждаются. 6.7. Новые средства Maple 106.7.1. Нелинейное программирование с ограничениями в Maple 10Maple 10 позволяет решать задачи нелинейного программирования с ограничениями с помощью функции NPSolve из пакета оптимизации Optimization. Наглядный пример из самоучителя по Maple 10 представлен на рис. 6.8. 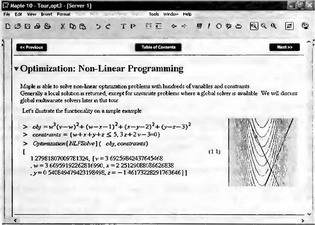 Рис. 6.8. Пример нелинейного программирования с ограничениями Целевая функция задана значением переменной obj, а ограничивающие условия заданы переменной constraints. Решение очевидно и иллюстрируется контурным графиком функции и линиями ограничения. 6.7.2. Нелинейный метод наименьших квадратов в Maple 10Большим подспорьем в решении задач нелинейной регрессии стала реализация в Maple 9.5/10 нелинейного метода наименьших квадратов. Для Maple 9.5 эта реализация уже была описана. Рис. 6.9 иллюстрирует применение функции LSSolve для выполнения нелинейной регрессии общего вида. Этот пример также взят из самоучителя по Maple 10. 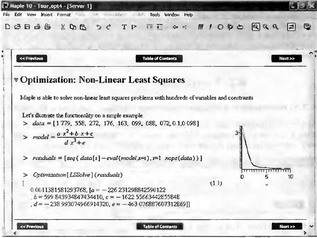 Рис. 6.9 Пример нелинейной регрессии в Maple Данные data представляют собой ординаты зависимости y(i), где i задается целыми числами, начиная от 1 и до значения, равного числу чисел в векторе данных. Исходная функция задана переменной model. Возвращается значение погрешности и вычисленные параметры регрессионной зависимости. Расчет хорошо иллюстрируется графиком этой зависимости и исходными точками. 6.7.3. Глобальная оптимизация и пакет Global Optimization ToolboxБольшинство методов оптимизации способно отыскивать локальные экстремумы. Например, это позволяет функция NLPSolve из встроенного пакета оптимизации. Меняя точку начального выбора (инициализации) можно найти и глобальный экстремум для простых функций. Но в Maple 10 есть возможность поиска глобального экстремума с помощью новой функции Global Solve пакета глобальной оптимизации, который можно найти в Интернете на сайте разработчика Maple 10. Пример этого для многоэкстремальной функции двух переменных представлен на рис. 6.10. 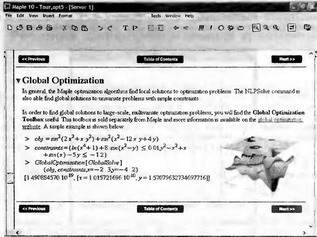 Рис. 6.10. Пример глобальной оптимизации многоэкстремальной функции двух переменных Подлежащая глобальной оптимизации функция представлена значением переменной obj. Ее многоэкстремальный характер обусловлен синусоидальными компонентами. Ограничения заданы переменной constraints. 6.7.4. Применение ассистента оптимизации Maple 10Для наглядного решения задач оптимизации можно применить маплет-ассистент оптимизации системы Maple 10. Ограничимся примером оптимизации многоэкстремальной функции одной переменной без ограничений — рис. 6.11. Такой вид окно имеет после ввода оптимизируемой функции с помощью кнопки Edit в области Objective Function. Выбор метода и прочие установки осуществлены по умолчанию (за исключением задания поиска максимума опцией Maximize). 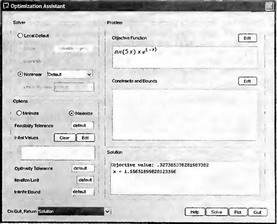 Рис. 6.11. Окно ассистента оптимизации с заданной функцией Чтобы проверить, что же нашел ассистент оптимизации, желательно построить график функции. Для этого достаточно активизировать кнопку Plot в окне рис. 6.11. Будет построен график в области оптимизации. Расширив область графика до значений x от 0 до 6 получим график, представленный на рис. 6.12. Нетрудно заметить, что найден глобальный максимум в точке, отмеченной кружком. 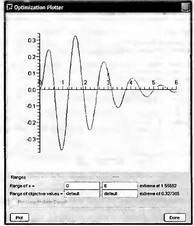 Рис. 6.12. График функции с помеченной точкой глобального максимума |
|
||
| Главная | В избранное | Наш E-MAIL | Добавить материал | Нашёл ошибку | Наверх | ||||
|
|
||||
