|
||||
|
|
Глава 7Решение дифференциальных уравнений Дифференциальные уравнения лежат в основе математического моделирования различных, в том числе физических, систем и устройств [1, 38, 46]. Решению таких уравнений посвящена эта глава. В ней рассмотрено как аналитическое, так и численное решение дифференциальных уравнений различного вида — линейных и нелинейных, классических и специальных, например, в частных производных и с учетом двухсторонних граничных условий. Описание сопровождается множеством наглядных примеров, реализованных в СКМ Maple 9.5/10. 7.1. Введение в решение дифференциальных уравнений7.1.1. Дифференциальные уравнения первого порядкаДифференциальные уравнения (ДУ) это уравнения, связывающие неизвестную функцию с какими либо ее производными и, возможно, с независимыми переменными. Если неизвестная функция зависит только от одной независимой переменной, то такое уравнение называется обыкновенным дифференциальным уравнением, а если от двух и более многих независимых переменных — дифференциальным уравнением в частных производных. Простейшее дифференциальное уравнение первого порядка в общем случае имеет множество решений в виде зависимостей y(х). Однако можно получить единственное решение, если задать начальные условия в виде начальных значений х0 и у0= у(х0). Это решение может быть аналитическим, конечно-разностным или численным. 7.1.2. Решение дифференциального уравнения радиоактивного распадаВ качестве примера аналитического решения дифференциального уравнения первого порядка (файл der) запишем дифференциальное уравнение радиоактивного распада атомов (N — число атомов в момент времени t, g=1/c): > restart: deq:=diff(N(t),t)=-g*N(t);
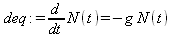 Используя функцию dsolve, которая более подробно будет описана чуть позже, получим его общее аналитическое решение: > dsolve(deq, N(t));N(t)=_C1e(-gtf) В решении присутствует произвольная постоянная _С1. Но ее можно заметить на постоянную N(0)=N0, означающую начальное число атомов в момент t=0: > dsolve({deq,N(0)=No},N(t));N(t)=Noe(-gt) Если конкретно N0=100 и g=4, то получим: > No := 100; g:=3;Nо:=100 g:=3 Хотя dsolve выдает решение N(t) в символьном виде, оно пока недоступно для построения графика этого решения или просто вычисления в любой точке. Однако, используя функции assign или subs можно сделать это решение доступным. Например, используем такую конструкцию: > s: =dsolve({ deq, N(0) =-No}, N (t)); assign(s);s: = N(t) = 100 e(-3t) Теперь мы можем воспользоваться полученной зависимостью N(t) и построить график ее: > plot(N(t),t=0..3,color=black); Этот график, который читатель может просмотреть сам, описывает хорошо известным апериодическим экспоненциальный закон уменьшения числа атомов вещества в ходе его радиоактивного распада. Подобные зависимости, кстати, характерны для напряжения на конденсаторе С при его разряде через резистор R, для тока в LA-цепи и для многих простых физических явлений, описывающихся дифференциальным уравнением первого порядка. 7.1.3. Модели популяций Мальтуса и Ферхюльса-ПирлаЕще одним классическим примером применения дифференциального уравнения первого порядка является давно известная и довольно грубая модель популяции Мальтуса. Не вдаваясь в хорошо известное описание этой модели, отметим, что она описывает численность особей или их биомассу x(t) в любой момент времени (для момента времени х(0)=N) Эта зависимость характеризуется коэффициентами рождаемости α и смертности β. При этом вводится их разность k=α-β. Представим задание дифференциального уравнения динамики популяций по модели Мальтуса и его решение в аналитическом виде: > restart:deq := diff(х(t),t) - k*x(t)=0; 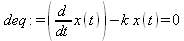 > dsol1 := dsolve({deq,x(0)=N});dsol1 := x(t) = Ne(k1) Нетрудно заметить, что решение этого уравнения аналогично решению дифференциального уравнения радиоактивного распада и описывается также экспоненциальной функций. Однако, в зависимости от того, какой фактор (рождаемость или смертность) преобладает наблюдается либо экспоненциальный рост, либо экспоненциальный спад биомассы популяций. Более правдоподобную модель популяций предложили Ферхюльст и Пирл. Эта модель учитывает (коэффициентом внутривидовую конкуренцию и позволяет учесть приближение популяций к некоторому состоянию равновесия. На рис. 7.1 представлено дифференциальное уравнение динамики популяций Ферхюльста-Пирла. Решения приведены в общем виде, а также для k=g= k/g=1 и разных x(0)=1, 0.5 и 2.  Рис. 7.1. Моделирование популяций по модели Ферхюльста и Пирла Поведение системы зависит от соотношения k/g и x(0)=N. При их равенстве количество биомассы популяции не меняется. При N>k/g биомасса экспоненциально уменьшается, приближаясь к значению k/g, а при N<k/g она экспоненциально возрастает, также приближаясь к k/g. 7.1.4. Системы дифференциальных уравненийВстроенные в математические системы функции обычно решают систему из обыкновенных дифференциальных уравнений (ОДУ), представленную в форме Коши: 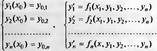 Здесь левая система задает начальные условия, а вторая представляет систему ОДУ. 7.1.5. Сведение ДУ высокого порядка к системам ОДУ первого порядкаЧасто встречаются ДУ высокого (n-го) порядка: y(n)=f(x, у, у', y'', …, y(n-1)),где y(x0)=y0, y'(x0) =y0,1, y''(x0)=y0,2, …, y(n-1)(x0)=y0,n-1Обозначив y1(х)=у(х), у2(х)=y'(x) …, yn(x)=y(n-1)(x)и y0,0= y(x0), y0,1=у'(х0), y0,n-1=y(n-1)(x0)Теперь решение этого уравнения можно свести к решению системы ОДУ: 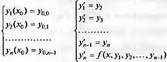 В таком виде ДУ n-го порядка может решаться стандартными средствами решения систем ОДУ, входящими в большинство математических систем. 7.1.6. Решение задачи на полет камняВ качестве примера аналитического решения системы дифференциальных уравнений рассмотрим постановку типичной физической задачи моделирования «Бросок камня», позволяющую описать полет камня, брошенного под углом к горизонту. Модель должна позволять: Вычислять положение камня в любой момент времени. Исходные данные: Масса камня, начальные координаты, начальная скорость и угол броска мяча. На основе содержательной модели разрабатывается концептуальная формулировка задачи моделирования. Применительно к нашей задаче движение камня может быть описано в соответствии с законами классической механики Ньютона. Гипотезы, принятые для модели: • камень будем считать материальной точкой массой m, положение которой совпадает с центром масс камня; • движение происходит в поле силы тяжести с постоянным ускорением свободного падения g и описывается уравнениями классической механики Ньютона; • движение камня происходит в одной плоскости, перпендикулярной поверхность Земли; • сопротивлением воздуха на первых порах пренебрегаем. В качестве параметров движения будем использовать координаты (х, у) и скорость v(vx, vy) центра масс камня. Концептуальная постановка задачи на основе принятых гипотез заключается в определении закона движения материальной точки массой m под действием силы тяжести, если известны начальные координаты точки х0 и ее начальная скорость v0 и угол броска α0. Таким образом, модель является простой — объект, как материальная точка, не имеет внутренней структуры. Учитывая типичные скорости и высоту броска камня, можно считать постоянным ускорение свободного падения. Переход от трехмерных координат к плоскости значительно упрощает решение задачи. Он вполне допустим, если камень не подкручивается при броске. Пренебрежение сопротивлением воздуха, как будет показано далее, приводит к значительной систематической ошибке результатов моделирования. Теперь перейдем к составлению математической модели объекта — совокупности математических соотношений, описывающих его поведение и свойства. Из законов и определяющих выражений предметной дисциплины формируются уравнения модели. По оси x на камень не действуют никакие силы, по оси y — действует сила тяжести. Согласно законам Ньютона имеем уравнения движения по оси x и оси y. при следующих начальных условиях x(0)=x0, y(0)=y0, vx(0)=v0∙cos α0, vy(0)=v0∙sin α0.Надо найти зависимости x(t), y(y), vx(r), vy(t). Математическая постановка решения задачи в нашем случае соответствует решению задачи Коши для системы обыкновенных дифференциальных уравнений с заданными начальными условиями. Известно, что решение задачи Коши существует и что оно единственное. Количество искомых переменных равно количеству дифференциальных уравнений. Таким образом, математическая модель корректна. Решение этой задачи есть в любом учебнике физики. Тем не менее, выполним его средствами системы Maple. Из (7.2) запишем систему ОДУ первого порядка: После интегрирования получим: Определив константы интегрирования из начальных условий, окончательно запишем: 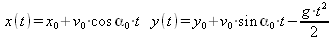 Из аналитического решения вытекает, что полет камня при отсутствии сопротивления воздуха происходит строго по параболической траектории, причем она на участках полета камня вверх и вниз симметрична. Необходимые для расчета уравнения заданы в параметрической форме — как зависимости от времени, что, кстати говоря, облегчает моделирование по ним полета камня. Немного позже мы решим эту задачу, используя средства Maple 9.5 для решения систем дифференциальных уравнений. 7.1.7. Классификация дифференциальных уравненийДифференциальные уравнения могут быть самого разного вида. На рис. 7.2 представлен раздел справки Maple 9.5 с классификацией дифференциальных уравнений. В ней представлено: • 20 дифференциальных уравнений первого порядка; • 25 дифференциальных уравнений второго порядка; • 6 типов дифференциальных уравнений высшего порядка; • основные функции решения дифференциальных уравнений.  Рис. 7.2. Классификация дифференциальных уравнений Эта классификация охватывает большую часть классических дифференциальных уравнений, которые используются в математике и в математической физике. Следует отметить, что речь не идет об отдельных функциях по решению таких уравнений частного вида, а о примерах составления соответствующих уравнений и решении их с помощью небольшого числа функций системы Maple 9.5. В качестве примера работы с классификатором выберем решение дифференциального уравнения Бернулли. Для этого активизируем на рис. 7.2 гиперссылку с его именем — Bernoulli. Появится окно справки по этому уравнению, показанное на рис. 7.3 с открытой позицией меню Edit.  Рис. 7.3. Окно справки по решению дифференциального уравнения Бернулли С помощью команды Copy Examples в позиции Edit меню можно перенести примеры решения с окна справки в буфер Clipboard операционной системы Windows. После этого командой Paste в меню Edit окна документа можно перенести примеры в текущий документ — желательно (но не обязательно) новый. Теперь можно наблюдать решение выбранного дифференциального уравнения — рис. 7.4.  Рис. 7.4. Пример решения дифференциального уравнения Бернулли из справки Возможность выбора и решения с полсотни классических дифференциальных уравнений различного типа дает системе Maple 9.5 преимущества, которые по достоинству оценят пользователи, заинтересованные в знакомстве с такими уравнениями и в их использовании. В Maple 9.5 средства решения дифференциальных уравнений подверглись значительной переработке. Введены новые методы решения для дифференциальных уравнений Абеля, Риккати и Матье, новые методы инициализации и решения уравнений с кусочными функциями, улучшены алгоритмы решения численными методами. Детальное описание этих новинок можно найти в справке по разделу What's New…. Это относится и к версии Maple 10. 7.1.8. Функция решения дифференциальных уравнений dsolveMaple позволяет решать одиночные дифференциальные уравнения и системы дифференциальных уравнений как аналитически, так и в численном виде. Разработчиками системы объявлено о существенном расширении средств решения дифференциальных уравнений и о повышении их надежности в смысле нахождения решений для большинства классов дифференциальных уравнений. Для решения системы простых дифференциальных уравнений (задача Коши) используется функция dsolve в разных формах записи: dsolve(ODE) dsolve(ODE, y(x), extra_args) dsolve({ODE, ICs}, y(x), extra_args) dsolve({sysODE, ICs}, {funcs}, extra_args) Здесь ODE — одно обыкновенное дифференциальное уравнение или система из дифференциальных уравнений первого порядка с указанием начальных условий, у(х) —функция одной переменной, Ics — выражение, задающее начальные условия, {sysODE} —множество дифференциальных уравнений, {funcs} — множество неопределенных функций, extra_argument —опция, задающая тип решения. Параметр extra_argument задает класс решаемых уравнений. Отметим основные значения этого параметра: • exact — аналитическое решение (принято по умолчанию); • explicit — решение в явном виде; • system — решение системы дифференциальных уравнений; • ICs — решение системы дифференциальных уравнений с заданными начальными условиями; • formal series — решение в форме степенного многочлена; • integral transform — решение на основе интегральных преобразований Лапласа, Фурье и др.; • series — решение в виде ряда с порядком, указываемым значением переменной Order; • numeric — решение в численном виде. Возможны и другие опции, подробное описание которых выходит за рамки данной книги. Его можно найти в справке по этой функции, вызываемой командой ?dsolve. Для решения задачи Коши в параметры dsolve надо включать начальные условия, а при решении краевых задач — краевые условия. Если Maple способна найти решение при числе начальных или краевых условий меньше порядка системы, то в решении будут появляться неопределенные константы вида _С1, _С2 и т.д. Они же могут быть при аналитическом решении системы, когда начальные условия не заданы. Если решение найдено в неявном виде, то в нем появится параметр _Т. По умолчанию функция dsolve автоматически выбирает наиболее подходящий метод решения дифференциальных уравнений. Однако в параметрах функции dsolve в квадратных скобках можно указать предпочтительный метод решения дифференциальных уравнений. Допустимы следующие методы: > `dsolve/methods`[1];[quadrature, linear, Bernoulli, separable, inverse_linear, homogeneous, Chini, lin_sym, exact, Abel, pot_sym ] Более полную информацию о каждом методе можно получить, используя команду ?dsolve,method и указав в ней конкретный метод. Например, команда ?dsolve,linear вызовет появление страницы справочной системы с подробным описанием линейного метода решения дифференциальных уравнений. 7.1.9. Уровни решения дифференциальных уравненийРешение дифференциальных уравнений может сопровождаться различными комментариями. Команда infolevel[dsolve] := n: где n — целое число от 0 до 5 управляет уровнями детальности вывода. По умолчанию задано n = 0. Значение n = 5 дает максимально детальный вывод. Производные при записи дифференциальных уравнений могут задаваться функцией diff или оператором дифференцирования D. Выражение sysODE должно иметь структуру множества и содержать помимо самой системы уравнений их начальные условия. Читателю, всерьез интересующемуся проблематикой решения линейных дифференциальных уравнений, стоит внимательно просмотреть разделы справки по ним и ознакомиться с демонстрационным файлом linearoade.mws, содержащим примеры решения таких уравнений в закрытой форме. 7.2. Примеры решения дифференциальных уравнений7.2.1. Примеры аналитического решение ОДУ первого порядкаОтвлекшись от физики, приведем несколько примеров на составление и решение дифференциальных уравнений первого порядка в аналитическом виде (файл dea): > dsolve(diff(y(х),х)-а*х=0, y(х)); 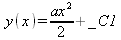 > dsolve(diff(y(х),х)-y(х)=ехр(-х), y(х)); 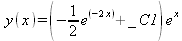 > dsolve(diff(y(х),х)-y(х)=sin(х)*х, y(х)); 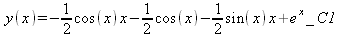 > infolevel[dsolve] := 3: > dsolve(diff(y(x),x)-y(x)=sin(x)*x, y(x)); Methods for first order ODEs: Trying classification methods — trying a quadrature trying 1st order linear <- 1st order linear successful 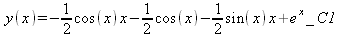 Обратив внимание на вывод в последнем примере. Он дан при уровне вывода n=3 Следующие примеры иллюстрируют возможность решения одного и того же дифференциального уравнения ode_L разными методами: > restart: ode_L := sin(x)*diff(y(x),x)-cos(x)*y(x)=0; 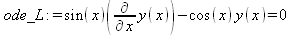 > dsolve(ode_L, [linear], useInt); 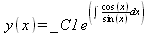 > value(%);y(x) = _C1 sin(x) > dsolve(od_L, [separable], useInt); 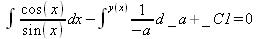 > value(%);ln(sin(x)) - ln(у(x)) + _C1 = 0 > mu := intfactor(ode_L); 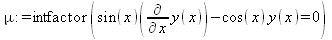 > dsolve(mu*ode_L, [exact], useInt);y(x) = -_C1 sin(x) Разумеется, приведенными примерами далеко не исчерпываются возможности аналитического решения дифференциальных уравнений. 7.2.2. Полет тела, брошенного вверхИз приведенных выше примеров видно, что для задания производной используется ранее рассмотренная функция diff. С помощью символа $ в ней можно задать производную более высокого порядка. В соответствии со вторым законом Ньютона многие физические явления, связанные с движением объектов, описываются дифференциальными уравнениями второго порядка. Ниже дан пример задания и решения такого уравнения (файл dem), описывающего движение тела, брошенного вверх на высоте h0 со скоростью v0 при ускорении свободного падения g: > restart; eq2:=diff(h(t),t$2) = -g; 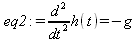 > dsolve({eq2,h(0)=h[0], D(h)(0)=v[0]},h(t));assign(s2); 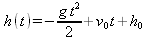 Итак, получено общее уравнение для временной зависимости высоты тела h(t). Разумеется, ее можно конкретизировать, например, для случая, когда g=9,8, h0=10 и v0=100: > g:=9.8: > s2:=dsolve({eq2,h(0)=10,D(h)(0)=100},h(t));assign(s2); 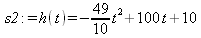 > plot(h(t),t=0..20,color=black); Зависимость высоты тела от времени h(t) представлена на рис. 7.5. Нетрудно заметить, что высота полета тела вначале растет и достигнув максимума начинает снижаться. Оговоримся, что сопротивление воздуха в данном примере не учитывается, что позволяет считать задачу линейной. Полученное с помощью Maple 9.5 для этого случая решение совпадает с полученным вручную в примере, описанном в разделе 7.1.3. 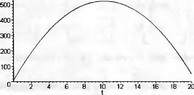 Рис. 7.5. Зависимость высоты полета тела от времени h(t) 7.2.3. Поведение идеального гармонического осциллятораЕще одним классическим применением дифференциальных уравнений второго порядка является решение уравнение идеального гармонического осциллятора (файл deio): > restart:eq3:=diff(y(t),t$2)=-omega^2*y(t); 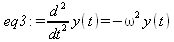 > dsolve(eq3,y(t));у(t) = _C1 sin(ω) + _C2 cos(ω) > s:=dsolve({eq3,y(0)=-1,D(y)(0)=1}, y(t)); 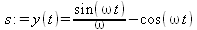 > assign(s);omega:=2;ω := 2 > plot(y(t),t=0..20,color=black); График решения этого уравнения (рис. 7.6) представляет хорошо известную синусоидальную функцию. Интересно, что амплитуда колебаний в общем случае отлична от 1 и зависит от значения у(0) — при у(0)=0 она равна 1 (в нашем случае синусоида начинается со значение у(0)=-1). Подобным осциллятором может быть LC-контур или механический маятник без потерь. 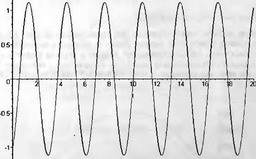 Рис. 7.6. Решение дифференциального уравнения идеального осциллятора 7.2.4. Дополнительные примеры решения дифференциальных уравнений второго порядкаНиже представлено решение еще двух дифференциальных уравнений второго порядка в аналитическом виде (de2a): > restart: dsolve(diff(y(x),x$2)-diff(y(x),x)=sin(x),y(x));у(x) = -½sin(x) + ½cos(x) + ex _C1 + _C2 > de:=m*diff(y(x),x$2)-k*diff(y(x),x); 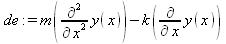 > yx0:=y(0)=0,y(1)=1;ух0:= у(0) = 0, у(1) = 1 > dsolve({de,yx0},y(x)); 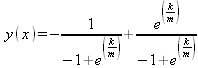 Ряд примеров на применение дифференциальных уравнений второго порядка при решении практических математических и физических задач вы найдете в главе 11. 7.2.5. Решение систем дифференциальных уравненийФункция dsolve позволяет также решать системы дифференциальных уравнений. Для этого она записывается в виде dsolve(ODE_sys, optional_1, optional_2,...) Здесь ODE_sys — список дифференциальных уравнений, образующих систему, остальные параметры опциональные и задаются по мере необходимости. Они могут задавать начальные условия, явно представлять искомые зависимости, выбирать метод решения и т.д. Детали задания опциональных параметров можно найти в справке. На рис. 7.7 представлено решение системы из двух дифференциальных уравнений различными методами — в явном виде, в виде разложения в ряд и с использованием преобразования Лапласа. Здесь следует отметить, что решение в виде ряда является приближенным. Поэтому полученные в данном случае аналитические выражения отличаются от явного решения и решения с применением преобразования Лапласа.  Рис. 7.7. Решение системы из двух дифференциальных уравнений различными методами Следует отметить, что, несмотря на обширные возможности Maple в области аналитического решения дифференциальных уравнений, оно возможно далеко не всегда. Поэтому, если не удается получить такое решение, полезно попытаться найти решение в численном виде. Практически полезные примеры решения дифференциальных уравнений, в том числе с постоянными граничными условиями, вы найдете в Главе 11. 7.2.6. Модель Стритера-Фелпса для динамики кислорода в водеВ качестве еще одного примера решении системы из двух дифференциальных уравнений рассмотрим модель Стритера-Фелпса, предложенную для описания динамики содержания растворенного в воде кислорода. Описание этой модели можно найти в [41]. Ниже представлено задание этой модели в виде системы из двух дифференциальных уравнений и их аналитическое решение (файл demp): > sys := diff(x1(t),t) = K1*(C-x1(t))-K2*x2(t), diff(x2(t),t) = -K2*x2(t); 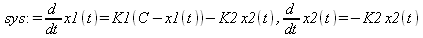 > dsol := dsolve({sys,x1(0) =a, x2(0)=b),{x1(t),x2(t)}); 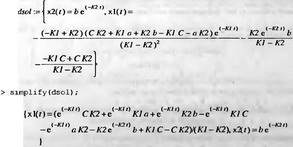 Здесь: x1(t) — концентрация в воде растворенного кислорода в момент времени t; x2(t) — концентрация биохимического потребления кислорода (БПК), С — концентрация насыщения воды кислородом, K1 — постоянная скорости аэрации, K2 — постоянная скорости уменьшения (БПК), a — начальное значение x1(t) и b — начальное значение х2(t) при t=0. В данном случае получены два варианта аналитического решения — основное и упрощенное с помощью функции simplify. Читатель может самостоятельно построить графики зависимостей x1(t) и x2(t). 7.3. Специальные средства решения дифференциальных уравнений7.3.1. Численное решение дифференциальных уравненийК сожалению, аналитического решения в общем случае нелинейные дифференциальные уравнения не имеют. Поэтому их приходится решать численными методами. Они удобны и в том случае, когда решение надо представить числами или, к примеру, построить график решения. Поясним принципы численного решения. Для этого вернемся к дифференциальному уравнению (7.1). Заменим приращение dx на малое, но конечное приращение dx=h. Тогда приращение dy будет равно Δy=h ∙ f(x, у).Если, к примеру, известно начальное значение у=у0, то новое значение у будет равно y1 = y0 + Δy = y0 + h∙f(x, y)Распространяя этот подход на последующие шаги решения получим конечно-разностную формулу для решение приведенного уравнения в виде: yi+1 = yi + h∙f(xi, yi).Эта формула известна как формула простого метода Эйлера первого порядка для решения дифференциального уравнения (7.1). Можно предположить (так оно и есть), что столь простой подход дает большую ошибку — отбрасываемый член порядка O(h2). Тем не менее, физическая и математическая прозрачность данного метода привела к тому, что он широко применяется на практике. Существует множество более совершенных методов решения дифференциальных уравнений, например, усовершенствованный метод Эйлера, метод трапеций, метод Рунге-Кутта, метод Рунге-Кутта-Фельберга и др. Ряд таких методов реализован в системе Maple и может использоваться при численном решении дифференциальных уравнений и систем с ними. Для решения дифференциальных уравнений в численном виде в Maple используется та же функция dsolve с параметром numeric или type=numeric. При этом решение возвращается в виде специальной процедуры, по умолчанию реализующей широко известный метод решения дифференциальных уравнений Рунге-Кутта-Фельберга порядков 4 и 5 (в зависимости от условий адаптации решения к скорости его изменения). Эта процедура называется rkf45 и символически выводится (без тела) при попытке решения заданной системы дифференциальных уравнений. Последнее достаточно наглядно иллюстрирует рис. 7.8. 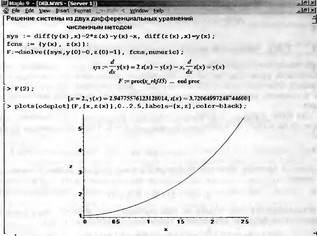 Рис. 7.8. Решение системы дифференциальных уравнений численным методом rkf45 с выводом графика решения Указанная процедура возвращает особый тип данных, позволяющих найти решение в любой точке или построить график решения (или решений). Для графического отображения Maple 9.5 предлагает ряд возможностей и одна из них представлена на рис. 7.8 — см. последнюю строку ввода. При этом используется функция plot[odeplot] из пакета odeplot, предназначенного для визуализации решений дифференциальных уравнений. Можно воспользоваться и функцией plot, выделив тем или иным способом (примеры уже приводились) нужное решение. В список параметров функции dsolve можно явным образом включить указание на метод решения, например опция method=dverk78 задает решение непрерывным методом Рунге-Кутта порядка 7 или 8. Вообще говоря, численное решение дифференциальных уравнений можно производить одним из следующих методов: • classical — одна из восьми версий классического метода, используемого по умолчанию; • rkf45 — метод Рунге-Кутта 4 или 5 порядка, модифицированный Фелбергом; • dverk78 — непрерывный метод Рунге-Кутта порядка 7 или 8; • gear — одна из двух версий одношагового экстраполяционного метода Гира; • mgear — одна из трех версий многошагового экстраполяционного метода Гира; • lsode — одна из восьми версий Ливенморского решателя жестких дифференциальных уравнений; • taylorseries — метод разложения в ряд Тейлора. Обилие используемых методов расширяет возможности решения дифференциальных уравнений в численном виде. Большинство пользователей Maple вполне устроит автоматический выбор метода решения по умолчанию. Однако в сложных случаях, или когда заведомо желателен тот или иной конкретный алгоритм численного решения, возможна прямая установка одного из указанных выше методов. С помощью параметра 'abserr'=aerr можно задать величину абсолютной погрешности решения, а с помощью 'minerr'=mine — минимальную величину погрешности. В большинстве случаев эти величины, заданные по умолчанию, оказываются приемлемыми для расчетов. Maple реализует адаптируемые к ходу решения методы, при которых шаг решения h автоматически меняется, подстраиваясь под условия решения. Так, если прогнозируемая погрешность решения становится больше заданной, шаг решения автоматически уменьшается. Более того, система Maple способна автоматически выбирать наиболее подходящий для решаемой задачи метод решения. Еще один пример решения системы дифференциальных уравнений представлен на рис. 7.9. Здесь на одном графике представлены зависимости y(x) и z(x) представляющие полное решение заданной системы. При этом процедура имеет особый вид listprocedure и для преобразования списка выходных данных в векторы решения Y и Z используется функция subs. 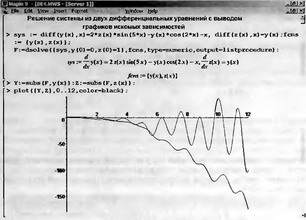 Рис. 7.9. Решение системы дифференциальных уравнений численным методом с выводом всех графиков искомых зависимостей Для решения достаточно сложных задач полезны специальная структура DESol для решения дифференциальных уравнений и инструментальный пакет SEtools, содержащий самые изысканные средства для графической визуализации результатов решения дифференциальных уравнений. Эти средства мы более подробно рассмотрим в дальнейшем. При решении некоторых задач физики и радиоэлектроники выбираемый по умолчанию шаг изменения аргумента х или t-h может привести к неустойчивости решения. Неустойчивости можно избежать рядом способов. Можно, например, нормировать уравнения, избегая необходимости использования малого шага. А можно задать заведомо малый шаг. Например, при method=classical для этого служит параметр stepsize=h. 7.3.2. Дифференциальные уравнения с кусочными функциямиСостоящие из ряда кусков кусочные функции широко используются при математическом моделировании различных физических объектов и систем. В основе такого моделирования обычно лежит решение дифференциальных уравнений, описывающих поведение объектов и систем. Покажем возможность применения кусочных функций для решения дифференциальных уравнений. Ниже представлено задание дифференциального уравнения первого порядка, содержащего кусочную функцию: > restart; > eq := diff(y(х), х)+ piecewise(х<х^2-3, ехр(х/2))*y(х); 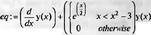 Используя функцию dsolve, выполним решение этого дифференциального уравнения: > dsolve(eq, y(х)); 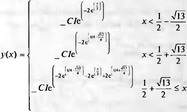 Нетрудно заметить, что результат получен также в форме кусочной функции, полностью определяющей решение на трех интервалах изменения х. Приведем пример решения дифференциального уравнения второго порядка с кусочной функцией: > eq := diff(y(х), х$2) + x*diff(y(x), х) + y(х) = piecewise(х > 0, 1); 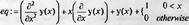 > dsolve(eq, y(х)); 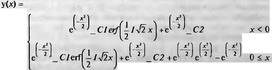 В заключении этого раздела приведем пример решения нелинейного дифференциального уравнения Риккати с кусочной функцией: > eq := diff(у(х), х)=piecewise(х>0, х)*у(х)^2; 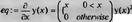 > dsolve({y(0)=1, eq}, y(х)); 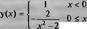 В ряде случаев желательна проверка решения дифференциальных уравнений. Ниже показано, как она делается для последнего уравнения: > simplify(eval(subs(%, eq))); 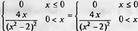 Как видно из приведенных достаточно простых и наглядных примеров, результаты решения дифференциальных уравнений с кусочными функциями могут быть довольно громоздкими. Это, однако, не мешает эффективному применению функций этого класса. 7.3.3. Структура неявного представления дифференциальных уравнений — DESolВ ряде случаев иметь явное представление дифференциальных уравнений нецелесообразно. Для неявного их представления в Maple введена специальная структура DESol(expr,vars) где exprs — выражение для исходной системы дифференциальных уравнений, vars — заданный в виде опции список переменных (или одна переменная). Структура DESol образует некоторый объект, дающий представление о дифференциальных уравнениях, чем-то напоминающее RootOf. С этим объектом можно обращаться как с функцией, то есть его можно интегрировать, дифференцировать, получать разложение в ряд и вычислять численными методами. На рис. 7.10 показаны примеры применения структуры DESol.  Рис. 7.10. Примеры применения структуры DESol Обратите внимание на последний пример — в нем структура DESol использована для получения решения дифференциального уравнения в виде степенного ряда. 7.4. Инструментальный пакет решения дифференциальных уравнений DEtools7.4.1. Средства пакета DEtoolsРешение дифференциальных уравнений самых различных типов — одно из достоинств системы Maple. Пакет DEtools предоставляет ряд полезных функций для решения дифференциальных уравнений и систем с такими уравнениями. Для загрузки пакета используется команда: > with(DEtools): Этот пакет дает самые изысканные средства для аналитического и численного решения дифференциальных уравнений и систем с ними. По сравнению с версией Maple V R5 число функций данного пакета в Maple 9.5 возросло в несколько раз. Многие графические функции пакета DEtools были уже описаны. Ниже приводятся полные наименования тех функций, которые есть во всех реализациях системы Maple: • DEnormal — возвращает нормализованную форму дифференциальных уравнений; • DEplot — строит графики решения дифференциальных уравнений; • DEplot3d — строит трехмерные графики для решения систем дифференциальных уравнений; • Dchangevar — изменение переменных в дифференциальных уравнениях; • PDEchangecoords — изменение координатных систем для дифференциальных уравнений в частных производных; • PDEplot — построение графиков решения дифференциальных уравнений в частных производных; • autonomous — тестирует дифференциальные уравнения на автономность; • convertAlg — возвращает список коэффициентов для дифференциальных уравнений; • convertsys — преобразует систему дифференциальных уравнений в систему одиночных уравнений; • dfieldplot — строит график решения дифференциальных уравнений в виде векторного поля; • indicialeq — преобразует дифференциальные уравнения в полиномиальные; • phaseportrait — строит график решения дифференциальных уравнений в форме фазового портрета; • reduceOrder — понижает порядок дифференциальных уравнений; • regularsp — вычисляет регулярные особые точки для дифференциальных уравнений второго порядка; • translate — преобразует дифференциальные уравнения в список операторов; • untranslate — преобразует список операторов в дифференциальные уравнения; • varparam — находит общее решение дифференциальных уравнений методом вариации параметров. Применение этих функций гарантирует совместимость документов реализаций Maple R5, 6 и 9. 7.4.2. Консультант по дифференциальным уравнениямДля выявления свойств дифференциальных уравнений в Maple 9.5 в составе пакета DEtools имеется консультант (адвизор), вводимый следующей функцией: odeadvisor(ODE) odeadvisor(ODE, y(х), [type1, type2,...], help) Здесь ODE — одиночное дифференциальное уравнение, y(x) — неопределенная (определяемая функция), type1, type2, … — опционально заданные множество типов, которые классифицируются и help — опционально заданное указание на вывод страницы справки по методу решения. Примеры работы с классификатором представлены ниже: > with(DEtools): ODE := x*diff(y(х),х)+а*y(х)+b*х^2; 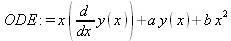 > odeadvisor(ODE);[_linear] > ОDE1 := x*diff(y(х)^2,х)+а*y(х)+b*х^2; 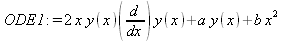 > odeadvisor(ODE1);[ rational, [_Abel, 2nd type, class В]] > ODE2 := diff(y(x),x,x,x)+D(g)(y(x))*diff(y(x),x)^3 + 2*g(y(x))*diff(y(x),x) *diff(y(x), x, x) + diff(f(x),x)*diff(y(x),x) + f(x)*diff(y(x),x,x) = 0; 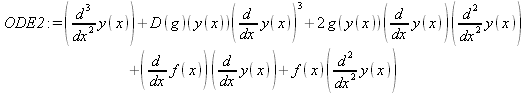 > odeadvisor(ODE2,у(x));[[_3rd_order, exact, _nonlinear], [_3rd order, reducible, _mu_y2]] 7.4.3. Основные функции пакета DEtoolsРассмотрим наиболее важные функции этого пакета. Функция autonomous(des,vars,ivar) тестирует дифференциальное уравнение (или систему) des. Ее параметрами, помимо des, являются независимая переменная ivar и зависимая переменная dvar. Следующие примеры поясняют применение этой функции: > autonomous(sin(z(t)-z(t)^2)*(D@@4)(z)(t)-cos(z(t))-5,z,t);true > DE:=diff(x(s),s)-x(s)*cos(arctan(x(s)))=arctan(s): > autonomous(DE,{x},s);false Ниже описание этой функции будет продолжено. Функция Dchangevar используется для обеспечения замен (подстановок) в дифференциальных уравнениях: Dchangevar(trans, deqns, с_ivar, n_ivar) Dchangevar(tran1, tran2, ..., tranN, deqns, с_ivar, n_ivar) В первом случае trans — список или множество уравнений, которые подставляются в дифференциальное уравнение, список или множество дифференциальных уравнений deqns. При этом civar — имя текущей переменной, n_ivar — имя новой переменной (его задавать необязательно). Во второй форме для подстановки используются уравнения tran1, tran2, … Ниже представлены примеры применения функции Dchangevar # Преобразование 1-го типа > Dchangevar(m(х) = l(х)*sin(x), n(x)=k(x), [D(m)(x)=m(x), (D@@2)(n)(x)=n(x)^2], x);[D(l)(x)sin(x) + l(x)cos(x) = l(x)sin(x), (D(2))(k)(x) = k(x)2 > Dchangevar(c=d, е=sin(f) , {D(с), (D@@2)(e)}, dummy);[D(d), (D(2))(sin(f))] # Преобразование 2-го типа > Dchangevar(t=arctan(tau), diff(x(t), t) = sin(t), t, tau);D(x)(arctan(x)) = sin(arctan(f))] > Dchangevar(x=sin(cos(t)),diff(y(x),x,x,x), x, t);(D(3))(y)(sin(cos(t))) # Преобразование 3-го типа > Dchangevar(x(t)=L*y(phi),diff(x(t),t$3) = tan(t),t,phi); 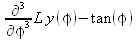 # Дополнительные примеры > Dchangevar({t=T*phi,x(t)=L*y(phi)},diff(x(t)), t$3)=tan(t),t,phi); 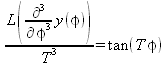 > de := diff(y(x),x$2) = y(x)*diff(y(x),x)/x; 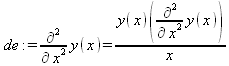 > Dchangevar({x=exp(t), y(x)=Y(t)},de,x,t); 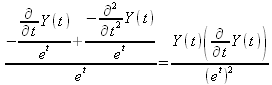 Следует отметить, что подстановки являются мощным средством решения дифференциальных уравнений. Нередки случаи, когда дифференциальное уравнение не решается без их применения. Функция нормализации ОДУ DEnormal синтаксически записывается в виде DEnormal(des, ivar, dvar) где des — система дифференциальных уравнений, ivar — независимая переменная и dvar — зависимая переменная. Применение этой функции поясняют следующие примеры: > DE := х^3*у(х)+х^2*(х-1)*D(y)(х)+50*х^3*(D@@2)(y)(x)=x*sin(x);DE := x3у(х) + x2(x-1)D(y)(x) + 50 x3(D(2))(y)(x) = x sin(x) > DE2 := convertAlg(DE,y(x));DE2 := [[x³, x³ - x², 50x³], x sin(x)] > DEnormal(DE,x,y(x)); 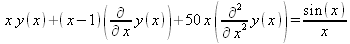 > DEnormal(DE2,х); 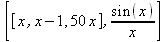 Функция convertAlg(des,dvar) возвращает список коэффициентов формы системы дифференциальных уравнений des с зависимыми переменными dvar. Это поясняют следующие примеры: > А : = diff(y(х),х)*sin(х) - diff(y(х),х) - tan(х)*y(х) = 5; 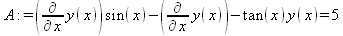 > convertAlg(А,y(х));[[-tan(x), sin(x) - 1], 5] > В := (D@@2)(y)(х)*cos(x) + (D@@2)(y)(х)*5*х^2;В := (D(2))(y)(x)cos(x) + 5(D(2))(y)(x)x2 > convertAlg(В,y(x));[[0, 0, cos(x) + 5 x²], 0] Для изменения переменных в системах дифференциальных уравнений используется функция convertsys: convertsys(deqns, inits, vars, ivar, yvec, ypvec) Здесь deqns — одно дифференциальное уравнение или список (множество), представляющие систему дифференциальных уравнений первого порядка, inits — множество или список начальных условий, vars — зависимые переменные, ivar — независимые переменные, yvec — вектор решений и ypvec — вектор производных. indicialeq(des,ivar,alpha,dvar) обеспечивает полиномиальное представление для линейного однородного дифференциального уравнения второго порядка des. Параметр alpha намечает точку сингулярности. > Y : = (2*х^2+5*х^3)*diff(y(х),х,х)+(5*х-х^2)*diff(y(х),х)+(1+х)*y(х)=0: > Y := convertAlg(Y, y(х));Y := [[1 + х, 5х - х², 2х² + 5х³], 0] > indicialeq(Y, х, -2/5, y(х)); 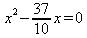 > indicialeq(Y, x, 0, y(x)); 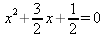 > indicialeq(Y, х, 1, y(х));x² - x = 0 Функция reduceOrder(des,dvar,partsol, solutionForm) обеспечивает понижение порядка дифференциального уравнения des (или системы уравнений, представленных списком или множеством) при зависимых переменных dvar, частном решении partsol (или списке частных решений) и флаге solutionForm, показывающем, что решение происходит явным методом (explicitly). Для демонстрации действия этой функции воспользуемся примером из ее справочной страницы: > de := diff(Y(х),х$3) - 6*diff(y(х),х$2) + 11*diff(y(х),х) - 6*y(х); 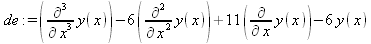 > sol:=exp(x);sol := еx > reduceOrder(de, y(х), sol); 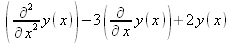 > reduceOrder(de, y(x), sol, basis); 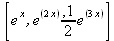 Функция regularsp(des,ivar,dvar) вычисляет регулярные особые (сингулярные) точки для дифференциального уравнения второго порядка или системы дифференциальных уравнений des. Следующий пример поясняет применение данной функции: > coefs := [21*(х^2-х+1), 0, 100*х^2*(х-1)^2]: > regularsp(coefs, х);[0, 1] Еще две функции пакета DEtools translate(des,ivar,pt,dvar) untranslate(des,ivar,pt,dvar) выполняют особую операцию трансляции дифференциального уравнения (или списка дифференциальных уравнений) из центрированного относительно 0 в центрированное относительно 1 и наоборот. С деталями этого специфического процесса заинтересованный читатель может познакомиться в справочной базе данных. И еще одна полезная функция пакета varparam(sols,v,ivar) находит общее решение дифференциального уравнения (или системы уравнений) sols методом вариации параметров. Параметр v задает правую часть уравнения; если он равен 0, ищется только частичное решение. > varparam([u1(х), u2(х)[LDV4]], g(x), х);{x1(t) = (e(-K1 t)C K2 + e(-K1 t)K1 a + e(-K1 t)K2 b – e(-K1 t)K1 C – e(-K1 t)a K2 – K2 e(-K1 t)b + K1 C – C K2)/(K1 – K2), x2(t) = b e(-K2 t) } Более подробную информацию об этих функциях читатель найдет в их справочных страницах, а также в информационном документе DEtools.mws, содержащем систематизированное описание пакета DEtools с многочисленными примерами его применения. 7.4.4. Дифференциальные операторы и их применениеСредствами пакета DEtools предусмотрена работа с дифференциальными операторами DF, которые дают компактное представление производных, например (файл difop): > restart; with(DEtools): > df := x*2*DF^2 - x*DF + (х^2 - 1);df := x²DF² - x DF + x² - 1 Данное выражение представляет собой дифференциальное уравнение второго порядка, записанное через дифференциальные операторы. С помощью функции diffop2de это уравнение можно преобразовать в обычное дифференциальное уравнение: > diffop2de(df,y(x),[DF,x]); 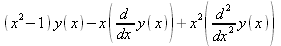 Теперь это уравнение можно решить с помощью функции dsolve: > dsolve(%, y(x));у(х) = _C1 х BesselJ(√2, x) + _С2 х BesselY(√2, x) Уравнения с дифференциальными операторами имеет вид степенного многочлена. Поэтому с ним можно выполнять множество операций, характерных для полиномов, например факторизацию, комплектование по степеням и др. В практике инженерных и научных расчетов дифференциальные операторы применяются довольно редко. Множество примеров с ними дано в файле примеров diffop.mws. 7.5. Графическая визуализация решений дифференциальных уравнений7.5.1. Применение функции odeplot пакета plotsДля обычного графического представления результатов решения дифференциальных уравнений может использоваться функция odeplot из описанного выше пакета plots. Эта функция используется в следующем виде: odeplot(s,vars, r, о) где s — запись (в выходной форме) дифференциального уравнения или системы дифференциальных уравнений, решаемых численно функцией dsolve, vars — переменные, r — параметр, задающий пределы решения (например, a..b) и о — необязательные дополнительные опции. На рис. 7.11 представлен пример решения одиночного дифференциального уравнения с выводом решения у(х) с помощью функции odeplot. 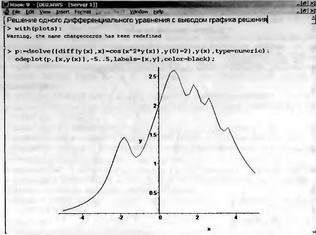 Рис. 7.11. Пример решения одиночного дифференциального уравнения В этом примере решается дифференциальное уравнение у'(х) = cos(x²y(x))при у(0)=2 и х, меняющемся от -5 до 5. Левая часть уравнения записана с помощью функции вычисления производной diff. Результатом построения является график решения y(x). В другом примере (рис. 7.12) представлено решение системы из двух нелинейных дифференциальных уравнений. Здесь с помощью функции odeplot строятся графики двух функций — y(х) и z(x). 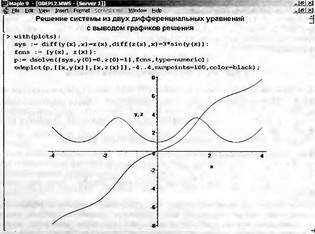 Рис. 7.12. Пример решения системы из двух дифференциальных уравнений В этом примере решается система: y'(х) = z(х), z'(x) = 3 sin(y(x))при начальных условиях y(0)=0, z(0)=1 и х, меняющемся от -4 до 4 при числе точек решения, равном 25. Иногда решение системы из двух дифференциальных уравнений (или одного дифференциального уравнения второго порядка) представляется в виде фазового портрета — при этом по осям графика откладываются значения у(х) и z(х) при изменении х в определенных пределах. Рисунок 7.13 демонстрирует построение фазового портрета для системы, представленной выше. 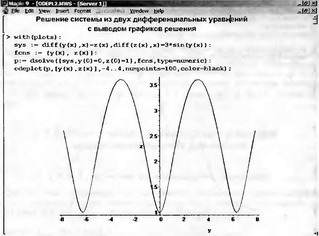 Рис. 7.13. Представление решения системы дифференциальных уравнений в виде фазового портрета Обычное решение, как правило, более наглядно, чем фазовый портрет решения. Однако для специалистов (например, в теории колебаний) фазовый портрет порою дает больше информации, чем обычное решение. Он более трудоемок для построения, поэтому возможность Maple быстро строить фазовые портреты трудно переоценить. 7.5.2. Функция DEplot из пакета DEtoolsСпециально для решения и визуализации решений дифференциальных уравнений и систем с дифференциальными уравнениями служит инструментальный пакет DEtools. В него входит ряд функций для построения наиболее сложных и изысканных графиков решения дифференциальных уравнений. Основной из этих функций является функция DEplot. Функция DEplot может записываться в нескольких формах: DEplot(deqns, vars, trange, eqns) DEplot(deqns, vars, trange, inits, eqns) DEplot(deqns, vars, trange, yrange, xrange, eqns) DEplot(deqns, vars, trange, inits, xrange, yrange, eqns) Здесь deqns — список или множество, содержащее систему дифференциальных уравнений первого порядка или одиночное уравнение любого порядка; vars — зависимая переменная или список либо множество зависимых переменных; trange — область изменения независимой переменной t; inits — начальные условия для решения; yrange — область изменения для первой зависимой пере- менной, xrange — область изменения для второй зависимой переменной; eqns — опция, записываемая в виде keyword=value. Замена имен переменных другими в данном случае недопустима. Эта функция обеспечивает численное решение дифференциальных уравнений или их систем при одной независимой переменной t и строит графики решения. Для автономных систем эти графики строятся в виде векторного поля направлений, а для неавтономных систем — только в виде кривых решения. По умолчанию реализуется метод Рунге-Кутта 4-го порядка, что соответствует опции method=classical[rk4], С функцией DEplot могут использоваться следующие параметры: • arrows=type — тип стрелки векторного поля ('SMALL', 'MEDIUM', 'LARGE', 'LINE' или 'NONE'); • colour, color = arfowcolour — цвет стрелок (задается 7 способами); • dirgrid = [integer,integer] — число линий сетки (по умолчанию [20, 20]); • iterations = integer — количество итераций, представленное целым числом; • linecolor, linecolor = line_info — цвет линии (задается 5 способами); • method='rk4' — задает метод решения ('euler', 'backeuler', 'impeuler' или 'rk4'); • obsrange = TRUE,FALSE — задает (при TRUE) прерывание вычислений, если кривая решения выходит из области обзора; • scene = [name,name] — задает имена зависимых переменных, для которых строится график; • stepsize=h — шаг решения, по умолчанию равный abs((b-a))/20, и представленный вещественным значением. 7.5.3. Решение системы дифференциальных уравнений модели Лотки-ВольтераЕще одна из моделей динамики популяций, известна как модель Лотки-Вольтера, описывает изменение популяции в биологической среде хищник-жертва. Эта модель позволяет описать периодическое колебательное изменение числа жертв и поедающих их хищников. На рис. 7.14 показано решение системы дифференциальных уравнений Лотки-Вольтера: x'(t) = x(t)(1 - y(t)), x'(t) = 0,3y(y)(x(t) - 1).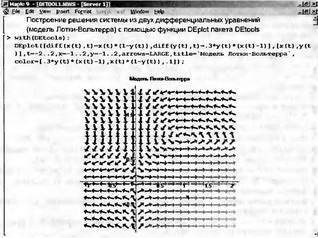 Рис. 7.14. Решение системы дифференциальных уравнений модели Лотки-Вольтерра с выводом в виде графика векторного поля Решение представлено в виде векторного поля, стрелки которого являются касательными к кривым решения (сами эти кривые не строятся). Обратите внимание на функциональную закраску стрелок векторного поля, делающую решение особенно наглядным (правда, лишь на экране цветного дисплея, а не на страницах книги). Еще интересней вариант графиков, представленный на рис. 7.15. Здесь помимо векторного поля несколько иного стиля построены фазовые портреты решения с использованием функциональной закраски их линий. Фазовые портреты построены для двух наборов начальных условий: x(0)=y(0)=1,2 и y(0)=1 и y(0)=0,9. 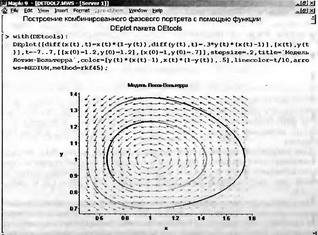 Рис. 7.15. Пример построения двух фазовых портретов на фоне векторного поля Читатель может легко дополнить этот пример выводом графиков временных зависимостей числа хищников и жертв и убедиться в том, что они действительно носят колебательный характер. При этом отличие фазовых портретов от эллиптической формы говорит о том, что форма колебаний заметно отличается от синусоидальной. Следует отметить, что функция DEplot может обращаться к другим функциям пакета SEtools для обеспечения специальных графических возможностей, таких как построение векторного поля или фазового портрета решения. В файле deplot.mws можно найти множество дополнительных примеров на применение функции Deplot. 7.5.4. Функция DEplot3d из пакета DEtoolsВ ряде случаев решение систем дифференциальных уравнений удобно представлять в виде пространственных кривых — например, линий равного уровня, или просто в виде кривых в пространстве. Для этого служит функция DEplot3d: DEplot3d(deqns, vars, trange, initset, o) DEplot3d(deqns, vars, trange, yrange, xrange, initset, o) Назначение параметров этой функции аналогично указанному для функции DEplot. Рис. 7.16 поясняет применение функции DEPlot3d для решения системы из двух дифференциальных уравнений с выводом фазового портрета колебаний в виде параметрически заданной зависимости x(t), y(t). В данном случае фазовый портрет строится на плоскости по типу построения графиков линий равной высоты (контурных графиков).  Рис. 7.16. Пример решения системы из двух дифференциальных уравнений с помощью функции DEplot3d Другой пример (рис. 7.17) показывает решение системы из двух дифференциальных уравнений с построением объемного фазового портрета. В этом случае используется трехмерная координатная система и графические построения соответствуют параметрическим зависимостям x(t), y(t) и z(t). Вид фазового портрета напоминает разворачивающуюся в пространстве объемную спираль. Функциональная окраска делает график пикантным, что, увы, теряется при черно-белом воспроизведении графика.  Рис. 7.17. Пример решения системы из двух дифференциальных уравнений с построением трехмерного фазового портрета Возможности функции DEplot3d позволяют решать системы, состоящие более чем из двух дифференциальных уравнений. Однако в этом случае число решений, представляемых графически, выходит за пределы возможного для трехмерной графики. При этом от пользователя зависит, какие из зависимостей опускаются при построении, а какие строятся. В файле deplot3d.mws есть ряд дополнительных примеров на применение функции Deplot3d. 7.5.5. Графическая функция dfieldplotГрафическая функция dfieldplot служит для построения поля направления с помощью векторов по результатам решения дифференциальных уравнений. Фактически эта функция как бы входит в функцию DEplot и при необходимости вызывается последней. Но она может использоваться и самостоятельно, что демонстрирует рис. 7.18, на котором показан пример решения следующей системы дифференциальных уравнений: x'(t)=x(t)(1-у(t)), у'(t)=0,3у(t)(х(t)-1). 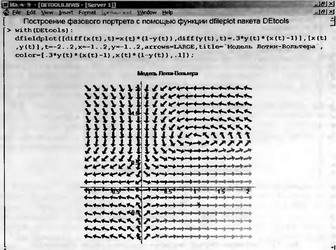 Рис. 7.18. Построение фазового портрета в виде графика векторного поля Обратите внимание на использование опций в этом примере — в частности, на вывод надписи на русском языке. В целом список параметров функции phaseportrait аналогичен таковому для функции DEplot (отсутствует лишь задание начальных условий). 7.5.6. Графическая функция phaseportraitГрафическая функция phaseportrait служит для построения фазовых портретов по результатам решения одного дифференциального уравнения или системы дифференциальных уравнений deqns. Она задается в следующем виде: phaseportrait(deqns,vars,trange,inits,о) При задании уравнений достаточно указать их правые части. На рис. 7.19 представлен пример применения функции phaseportrait для решения системы из трех дифференциальных уравнений первого порядка. 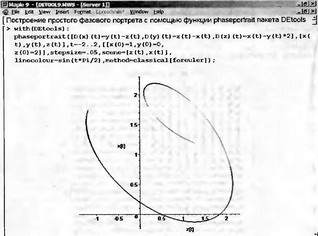 Рис. 7.19. Построение фазового портрета с помощью функции phaserportrait В этом примере система дифференциальных уравнений задана с помощью оператора дифференцирования D. Функциональная окраска линии фазового портрета достигается использованием параметра linecolor в правой части которой задана формула для цвета. Еще более интересный пример решения дифференциального уравнения представлен на рис. 7.20. Здесь построены фазовые портреты для асимптотических решений. 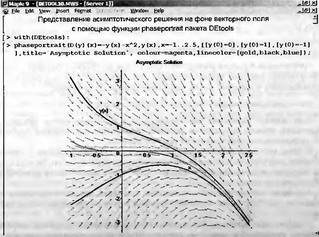 Рис. 7.20. Построение асимптотического решения на фоне графика векторного поля В целом надо отметить, что возможности визуализации решений дифференциальных уравнений с помощью системы Maple весьма велики и приведенные выше примеры лишь частично иллюстрируют сказанное. 7.6. Углублённый анализ дифференциальных уравнений7.6.1. Задачи углубленного анализа ДУMaple 9.5 существенно доработан по части решения дифференциальных уравнений (ДУ) и систем с ДУ. Эта доработка, прежде всего, направлена на получение верных решений как можно большего числа ДУ разных классов и систем с ДУ. В частности расширен круг нелинейных дифференциальных уравнений, для которых система Maple 9.5 способна дать аналитические решения. Весь арсенал средств решения ДУ и методика их применения вполне заслуживают отражения в отдельной большой книге. Мы ограничимся описанием только трех средств системы Maple — проверки ДУ на автономность, углубленным анализом решения с помощью контроля уровня выхода и получением приближенного полиномиального аналитического решения. 7.6.2. Проверка ДУ на автономностьОдиночное дифференциальное уравнение или система дифференциальных уравнений называется автономной, если их правая часть явно не зависит от независимой переменной. Для автономных дифференциальных уравнений или систем при построении графиков решений функцией DEplot не обязательно задавать начальные условия, но нужно указывать диапазон изменения искомых переменных. Для проверки уравнений (или систем) на автономность используется функция autonomous(des,vars, ivar) где des — заданное дифференциальное уравнение или (в виде списка) система дифференциальных уравнений, vars — зависимые переменные и ivar — независимая переменная. Если система автономна, то эта функция возвращает true, в противном случае false. Примеры: > dif1:=diff(х(t),t)=x(t)*(1-y(t)); dif2:=diff(y(t),t)=.3*y(t)*(x(t)-1); 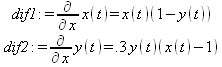 > autonomous({dif1,dif2),[x(t),y(t)],t);true > autonomous(diff(x(t),t)=sin(t),x,t);false В первом случае система дифференциальных уравнений (модель Лотки-Вольтерра) автономна, а во втором случае дифференциальное уравнение не автономно. 7.6.3. Контроль уровня вывода решения ДУДля углубленного анализа аналитического решения ДУ (или системы ДУ) можно использовать специальную возможность управления уровнем вывода решения с помощью системной переменной infolevel(dsolve):=level. Значение level=all дает обычный вывод решения без комментариев, уровень 1 зарезервирован для информации, которую может сообщить пользователь, уровень 2 или 3 дает более детальный вывод (включая сообщения об использованном алгоритме и технике решения) и, наконец, уровни 4 и 5 дают наиболее детальную информацию (если таковая есть в дополнение к той информации, которую дает уровень 2 или 3). Приведем пример аналитического решения ДУ третьего порядка с контролем уровня вывода решения (файл deil): > myDE:= x^2 * diff(y(х),х,х,х) - 2*(n+1)*x*diff(y(х), х, х) + (а*х^2+6*n)*diff(y(х),х)-2*а*х-y(х) = 0; 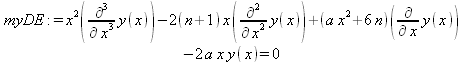 > infolevel[dsolve] := all: dsolve(myDE); 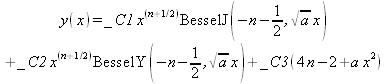 > infolevel[dsolve] := 1:dsolve(myDE); <- No Liouvillian solutions exists 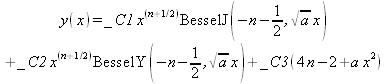 > infolevel[dsolve] := 3:dsolve(myDE); Methods for third order ODEs: -- Trying classification methods -- trying a quadrature checking if the LODE has constant coefficients checking if the LODE is of Euler type trying high order exact linear fully integrable trying to convert to a linear ODE with constant coefficients Equation is the LCLM of -2*x/(2*(2*n-1)/а+х^2)*y(x)+diff(y(x), x), a*y(x)-@KOD = 2*n/x*diff(y(x),x)+diff(diff(y(x),x),x) checking if the LODE is of Euler type -> Attemtping a differential factorization trying exponential solutions checking if the LODE is of Euler type 1, exponential solutions found exponential solutions successful <- differential factorization successful -> Tackling the linear ODE "as given": trying a quadrature checking if the LODE has constant coefficients checking if the LODE is of Euler type trying a symmetry of the form [xi=0, eta=F(x)] checking if the LODE is missing 'y' -> Trying a Liouvillian solution using Kovacic's algorithm <- No Liouvillian solutions exists -> Trying a solution in terms of special functions: -> Bessel <- Bessel successful <- special function solution successful <- successful solving of the linear ODE "as given" <- solving the LCLM ode successful 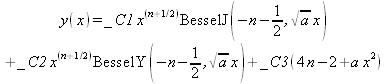 В данном случае повышение уровня вывода до 4 или 5 бесполезно, поскольку вся информация о решении сообщается уже при уровне 2 (или 3). 7.6.4. Приближенное полиномиальное решение дифференциальных уравненийВо многих случаях аналитические решения даже простых ДУ оказываются весьма сложными, например, содержат специальные математические функции. При этом нередко полезна подмена такого решения другим, тоже аналитическим, но приближенным решением. Наиболее распространенным приближенным решением в этом случае может быть полиномиальное решение, то есть замена реального решения полиномом той или иной степени. При этом порядок полинома задается значением системной переменной Order, а для получения такого решения функция dsolve должна иметь параметр series. На рис. 7.21 представлено решение ДУ третьего порядка различными методами: точное аналитическое и приближенное в виде полинома с максимальным заданным порядком 10 и 60. График дает сравнение этих решений для зависимости у(t). 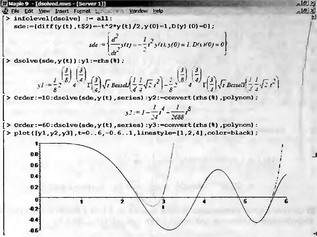 Рис. 7.21. Примеры решения ДУ третьего порядка Дадим небольшой комментарий. Нетрудно заметить, что точное аналитическое решение весьма сложно и содержит специальные функции Бесселя и гамма-функции. При порядке полинома 8 (он несколько меньше заданного максимального) решение практически совпадает с точным до значений t<2, а при максимальном заданном порядке 60 область совпадения расширяется до значений t<5,5. Затем приближенное решение резко отходит от точного. Этот пример с одной стороны иллюстрирует хорошо известный факт — быстрое нарастание погрешности полиномиального приближения за пределами области хорошего совпадений решений. С другой стороны он показывает, что степень полинома более 60 (и даже выше) вовсе не так уж бесполезна, как это утверждается во многих статьях и книгах по полиномиальному приближению. Точность полиномиальных вычислений Maple достаточно высока, чтобы обеспечить получение приближенных полиномиальных выражений со степенью порядка десятков и иногда даже сотен. Другое дело, что столь «длинный» полином не всегда удобен для аналитических расчетов, даже несмотря на его структурную простоту. 7.7. Решение дифференциальных уравнений специального вида7.7.1. Определение жестких систем дифференциальных уравненийВ последнее время особое внимание уделяется решению важного класса систем дифференциальных уравнений — жестких. Если представить систему дифференциальных уравнений в матричном виде у = Ах, то такая система относится к жесткой при выполнении следующих двух условий: • действительные части всех собственных значений матрицы А отрицательны, т. е. Re(λk)<0 (А = 0, 1, …, n-1); • величина s=max|Re(λk) |/min|Re(λk) (k=0, 1, …, n-1), именуемая жесткостью системы, должна быть велика. Жесткие системы впервые появились при решении систем дифференциальных уравнений химической кинетики. Решение таких систем представляется фрагментами с сильно отличающейся крутизной зависимостей. Нередко это случается и при анализе электрических цепей с резко отличными постоянными времени. Если шаг решения h сравним или больше наименьшей постоянной времени решения, то применение стандартных методов (например, Рунге-Кутта) с неизменным шагом приводит к большим погрешностям вычислений и даже к к расхождению вычислительного процесса, в ходе которого решение грубо отлично от существующего. Maple в большинстве случаев дает верное решение даже без указания метода решения. Это связано с тем, что система дифференциальных уравнений при решении его функцией dsolve анализируется и в зависимости от результатов анализа выбирается наиболее подходящий метод решения. Кроме того, большинство методов (например, самый распространенный rkf45) реализуют алгоритмы контроля погрешности вычислений и дробления шага решения, если погрешность оказывается больше заданной. В связи с указанным решение жестких систем дифференциальных уравнении средствами системы Maple не вызывает особых трудностей и может быть осуществлено даже при выборе не вполне удачного метода. Однако при этом возможны следующие ситуации: • может резко возрасти время вычислений из за чрезмерно сильного уменьшения шага решения; • может оказаться превышенным число итераций в ходе дробления шага; • для «особо жестких» систем адаптивный выбор шага может не помочь и погрешность решения будет большой. Во избежание этого рекомендуется при решении жестких систем дифференциальных уравнений все же пользоваться специально для них созданными методами, например методом Розенброка (опция method=rosenbrock для функции dsolve). 7.7.2. Примеры решения жестких систем дифференциальных уравненийВ качестве первого примера исследуем и решим следующую систему дифференциальных уравнений (файл sdes): > deq2 := diff(u(t),t) = -11*u(t)+9*v(t), diff(v(t),t) = 9*u(t)-11*v(t); 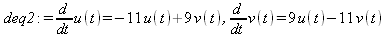 Загрузив пакет linalg вычислим собственные значения матрицы данной системы дифференциальных уравнений: > with(linalg): M:=matrix(2,2, [-11,9,9,-11]); 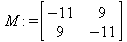 > ge:=eigenvalues(M);ge := - 2, -20 Они оказались отрицательными. Кроме того, очевидно, что значение жесткости данной системы s=10. Его трудно назвать очень большим, но в целом условия жесткости для данной системы выполняются. Теперь решим эту систему методом Розенберга. Решение представлено на рис. 7.22. Обратите внимание на то, что представлены две точки и график решения. К достоинствам реализации примененного метода относится отсутствие необходимости в составлении матрицы Якоби, которую приходится задавать при использовании ряда функций системы Mathcad, имеющихся для решения жестких систем дифференциальных уравнений [9]. 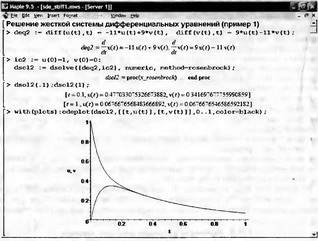 Рис. 7.22. Задание и решение жесткой системы дифференциальных уравнений (пример 1) Еще один пример задания и решения жесткой системы дифференциальных уравнений представлен на рис. 7.23. Собственные значения матрицы этой системы равны -2 и -1000, а жесткость системы s=500 (проверьте сами по аналогии с ранее приведенным примером). Таким образом, эта система намного жестче, чем система из первого примера. Обратите внимание на то, что она решается без задания метода решения, но с опцией stiff=true, вынуждающей Maple выбирать метод для решения жестких систем дифференциальных уравнений. 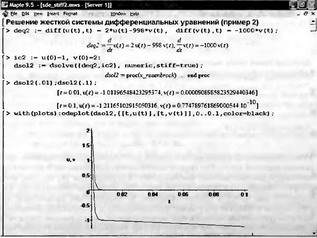 Рис. 7.23. Задание и решение жесткой системы дифференциальных уравнений (пример 2) 7.7.3. Пример решения системы жестких дифференциальных уравнений химической кинетикиЖесткие системы дифференциальных уравнений, часто описывают кинетику химических процессов, например, растворение веществ в растворах или смешивание газов. На рис. 7.24 показано решение жесткой системы из трех дифференциальных уравнений, описывающих один из типовых химических процессов — какой именно в данном случае не важно. 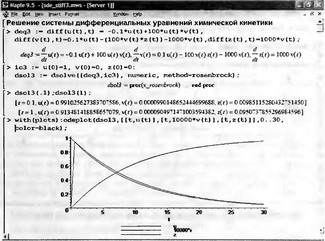 Рис. 7.24. Решение жесткой системы дифференциальных уравнений, описывающей кинетику химического процесса 7.7.4. Решение дифференциального уравнения Ван-Дер ПоляКлассическим примером нелинейного дифференциального уравнения второго порядка, относящегося к жесткому типу по большом значении некоторого параметра mu, относится уравнение Ван-Дер Поля. Важность этого уравнения заключается в том, что к нему довольно просто сводятся дифференциальные уравнения, описывающие динамику развития колебаний в различных колебательных системах, например, автогенераторах на электронных лампах, полевых и биполярных транзисторах. Пример задания и решения дифференциального уравнения Ван-Дер Поля при сравнительно малом mu=1 (и при выборе метода решения по умолчанию) представлен на рис. 7.25. Нетрудно заметить, что выбор Maple пал на метод rkf45 и что этот метод не очень удачен даже для этого метода с mu=1. Хотя общая форма колебаний (близкая к синусоидальной, но все же заметно искаженная) в интервале t от 0 до 20 просматривается, уже в данном случае видна нестабильность колебаний. При увеличен максимального значения t до 100 и более, нестабильность колебаний становится весьма заметна (проверьте это сами). 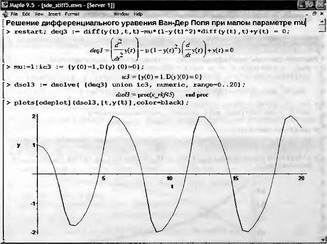 Рис. 7.25 Задание и решение дифференциального уравнения Ван-Дер Поля при сравнительно малом mu=1 Задание и решение дифференциального уравнения Ван-Дер Поля при большом mu=2000 (рис. 7.26) демонстрирует существенное изменение формы временной зависимости колебаний и их параметров. Теперь отчетливо виден разрывный характер колебаний, типичный для релаксационных колебаний. Моделирование колебаний в этом случае методом rkf45 уже невозможно и потому для решения задана опция stiff=true. При этом Maple взял за основу метод Розенброка. Он обеспечивает более качественное моделирование в системе Ван-Дер Поля. 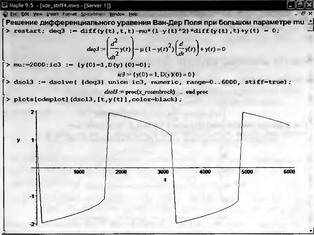 Рис. 7.26. Задание и решение дифференциального уравнения Ван-Дер Поля при большом mu=2000 Дополнительные примеры на решение жестких систем дифференциальных уравнений можно найти в разделах справки по решению таких уравнений. 7.7.5. Решение дифференциальных уравнении с двумя краевыми условиямиВ решении ряда математических задач нужно найти решение дифференциального уравнения с двумя краевыми условиями. Например, в физике это задача стрельбы по летящей цели. Обычно такая задача решается методом пристрелки, при котором методом проб с итерационным уточнением рассчитывается ряд вариантов решения и выбирается тот, у которого соблюдается начальное условие в начале решения и начальное условие в конце решения с заданной (в частности по умолчанию) погрешностью. Для такого решения используется функция dsolve в следующем виде: dsolve(odesys, numeric, vars, options) Здесь: • odesys — множество или список обыкновенных дифференциальных уравнений и двойных граничных условии; • numeric — опция, задающая решение в численном виде; • vars — опционально заданный параметр, задающий имя переменной в odesys; • options — опционально заданные равенства (в форме keyword=value), определяющие краевые условия. Пример решения дифференциального уравнения второго порядка с двумя граничными условиями представлен на рис. 7.27. Отчетливо видно, что найденная зависимость точно удовлетворяет краевым условиям. 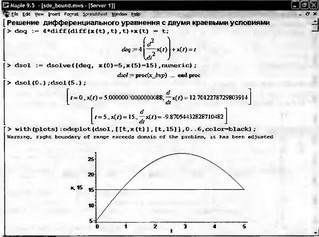 Рис. 7.27. Пример решения дифференциального уравнения второго порядка с двумя граничными условиями 7.8. Решение дифференциальных уравнений с частными производными7.8.1. Функция pdsolveВ Maple 9.5 имеется функция pdsolve для решения дифференциальных уравнений с частными производными. Она может использоваться в следующих формах записи: pdsolve(PDE, f, HINT, INTEGRATE, build) pdsolve(PDE_system, funcs, HINT, other_options) pdsolve(PDE_system, conds, numeric, other_options) pdsolve(PDE_system, conds, type=numeric, other_options) Эта функция введена вместо устаревшей функции pdesolve. В функции pdsolve используются следующие параметры: • PDE — одиночное дифференциальное уравнение с частными производными; • PDE system — система дифференциальных уравнений с частными производными; • conds — начальные или граничные условия; • f — неопределенная функция или имя; • funcs — (опция) множество или список с неопределенными функциями или именами; • HINT — (опция) равенство в форме HINT=argument, где аргумент может быть символом '+', '*', любым алгебраическим выражением или строкой 'strip'; • INTEGRATE — (опция) задает автоматическое интегрирование для множества ODEs (если PDE решается при разделении переменных; • build — опция, задающая попытку построения явного выражения для неопределенной функции, независимо от общности найденного решения; • numeric — ключевое слова, задающее решение в численном виде; • other options — другие опции. 7.8.2. Инструментальный пакет расширения PDEtoolДля решения дифференциальных уравнений с частными производными и его визуализации в Maple 9.5 служит специальный инструментальный пакет PDEtool: > with(PDEtools);[PDEplot, build, casesplit, charstrip, dchange, dcoeffs, declare, diff order, dpolyforin, dsubs, mapde, separability, splitstrip, splitsys, undeclare] Ввиду небольшого числа функций этого пакета приведем их определения: build(sol) — конструирует улучшенную форму решения, полученного функцией pdsolve; casesplit(sys, о1, o2, …) — преобразует форму дифференциального уравнения; charstrip(PDE, f) — находит характеристическую последовательность, дающую дифференциальное уравнение первого порядка; dchange(tr,expr,o1,o2,…) — выполняет замену переменных в математических выражениях или функциях; dcoeff(expr,y(x)) — возвращает коэффициенты полиномиала дифференциального уравнения; declare(expr) и др. — задает функцию для компактного ее отображения; difforder(a,x) — возвращает порядок дифференциала в алгебраическом выражении а; dpolyform(sys,no_Fn,opts) — возвращает полиномиальную форму для заданной системы sys не полиномиальных дифференциальных уравнений; dsubs(deriv1=a,…,expr) — выполняет дифференциальные подстановки в выражение expr; mapde(PDE,into,f) — создает карту PDE в различных форматах into с опциональным заданием имени неизвестной функции f; separability(PDE, F(x,y,…), '*') — определяет условия разделения для сумм или произведений PDE; splitstrip(PDE, f) — разделяет характеристическую последовательность на несоединенные поднаборы; splitsys(sys,funcs) — разделяет наборы уравнений (алгебраические и дифференциальные) на несоединенные поднаборы; undeclare(f(x),…) и др. — отменяет задание функции для компактного ее отображения. 7.8.3. Примеры решения дифференциальных уравнений с частными производнымиПримеры решения дифференциальных уравнений и систем с частными производными представлены ниже (файл pde): > restart: with(PDEtools): > PDE := x*diff(f(x, y), y) - diff(f(x,y),x)=f(x,y;^2*g(x)/h(y); 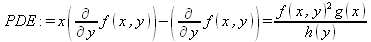 > ans := pdsolve(PDE); 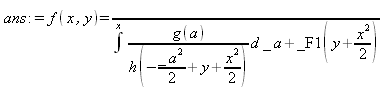 > PDE := S(x,y)*diff(S(x,y),y,x) + diff(S(x,y),x)*diff(S(x,y),y) = 1; 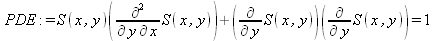 > struc := pdsolve(PDE, HINT=f(x)*g(y)); 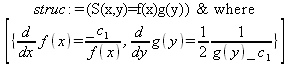 > build(struc); 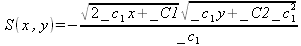 > pdsolve(PDE,HINT=P(x,y)^(1/2)); 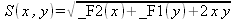 > PDE := diff(f(x,y,z), x) + diff(f(x,y,z), у)^2 = f(x,y,z)+z; 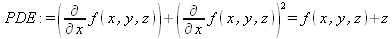 > pdsolve(PDE, HINT=strip); 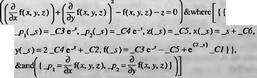 > myPDEsystem := [-y*diff(f(x,у,z,t),x) + z^2*diff(f(x,y,z,t),z) + 3*t*z*diff(f(x,y,z,t),t) - 3*t^2-4*f(x,y,z,t)*z = 0, -y*diff(f(x, y, z, t), y) - z*diff(f(x,y,z,t),z) - t*diff(f(x,y,z,t), t) + f(x,y,z,t) = 0, -x*diff(f(x, y, z, t), y) - diff(f(x,y,z,t),z)=0]: for _eq in myPDEsystem do _eq; od; 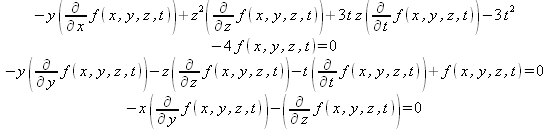 > sol := pdsolve(myPDEsystem); 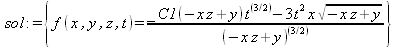 Обратите внимание на то, что в последнем примере из справки решена система дифференциальных уравнений в частных производных. 7.8.4. Функция PDEplot пакета DEtoolsОдна из важнейших функций пакета DEtools — DEtools[PDEplot] — служит для построения графиков решения систем с квазилинейными дифференциальными уравнениями первого порядка в частных производных. Эта функция используется в следующем виде: PCEplot(pdiffeq, var, i_curve, srange, o) PDEplot(pdrffeq, var, i_curve, srange, xrange, yrange, urange, o) Здесь помимо упоминавшихся ранее параметров используются следующие: pdiffeq — квазилинейные дифференциальные уравнения первого порядка (PDE), vars — независимая переменная и i_curve — начальные условия для параметрических кривых трехмерной поверхности. Помимо опций, указанных для функции DEplot, здесь могут использоваться следующие опции: • animate = true, false — включение (true) или выключение (false) режима анимации графиков; • basechar = true, false, ONLY — устанавливает показ начального условия на плоскости (х,у); • basecolor = b_color — устанавливает цвет базовых характеристик; • ic_assumptions — задание (в виде равенств или неравенств) ограничений на начальные условия для первых производных; • initcolor = i_color — инициализация цвета кривой начальных условий; • numchar = integer — залает число отрезков кривых, которое не должно быть меньше 4 (по умолчанию 20); • numsteps = [integer1, integer2] — задает число шагов интегрирования (по умолчанию [10,10]); • obsrange = true, false — прекращение интегрирования (true) при выходе отображаемой переменной за заданные пределы или продолжение интегрирования (false) в любом случае; • scene=[x,y,u(x,y)] — вывод обозначений координатных осей. С помощью параметров и опций можно задать множество возможностей для наглядной визуализации довольно сложных решений систем дифференциальных уравнений с частными производными. Следует отметить, что неправильное задание параметров ведет просто к выводу функции в строке вывода без построения графиков и нередко без сообщений об ошибках. Поэтому полезно внимательно просмотреть примеры применения этой функции — как приведенные ниже, так и в справке. 7.8.5. Примеры применения функции PDEplotРисунок 7.28 демонстрирует применение функции PDEplot. Этот пример из справки показывает, насколько необычным может быть решение даже простой системы дифференциальных уравнений в частных производных.  Рис. 7 28. Пример применения функции PDEplot В данном случае решение представлено трехмерной фигурой весьма нерегулярного вида. Другой пример использования функции PDEplot показан на рис. 7.29. Он иллюстрирует комбинированное построение графиков решения разного типа с применением функциональной закраски, реализуемой по заданной формуле с помощью опции initcolor.  Рис. 7.29. Построение комбинированного графика с помощью функции PDEplot Еще раз отметим, что, к сожалению, рисунки в данной книге не дают представления о цвете выводимых системой Maple графиков. Поэтому наглядность решений, видимых на экране монитора, существенно выше. 7.9. Сложные колебания в нелинейных системах и средах7.9.1. Пример нелинейной системы и моделирование колебаний в нейМногие системы (например, нелинейные оптические резонаторы, лазерные устройства и др.) описываются системами из более чем двух нелинейных дифференциальных уравнений. Колебания в таких системах нередко носят сложный нестационарный, а порою даже хаотический характер. Примером этого может служить анализ переходных процессов в системе, описываемой тремя дифференциальными уравнениями и представленной на рис. 7.30. 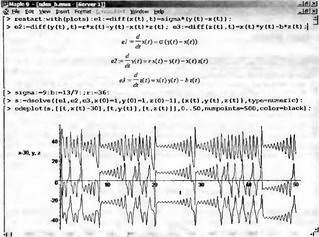 Рис. 7.30. Пример решения системы из трех нелинейных дифференциальных уравнений, создающей колебания сложной формы Поведение системы описывается тремя постоянными sigma, b и r, меняя которые можно получить самый различный вид временных зависимостей x(t), y(t) и z(t). Даже на ограниченном промежутке времени эти зависимости имеют весьма сложный и почти непредсказуемый характер и далеки от периодических колебаний. Нередко в них проглядывает фрактальный характер. 7.9.2. Фазовый портрет на плоскостиФункция odeplot позволяет получать не только графики временных зависимостей, но и фазовые портреты колебаний. Рисунок 7.31 показывает построение фазового портрета в плоскости (x, y). 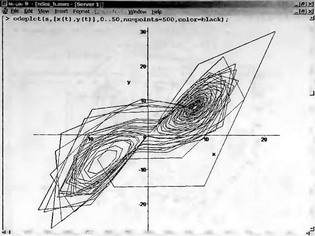 Рис. 7.31. Фазовый портрет колебаний на плоскости (х, у) Нетрудно заметить, что фазовый портрет отчетливо выделяет два фокуса, которые соответствуют слабым осцилляциям нарастающих почти гармонических колебаний, время от времени повторяющимся. В целом же фазовый портрет колебаний оказывается довольно запутанным и хорошо иллюстрирует развитие нестационарных компонент колебаний. 7.9.3. Фазовые портреты в пространствеМожно разнообразить представления о колебаниях, перейдя к построению трехмерных (пространственных) фазовых портретов. Они делают такое представление более полным. На рис. 7.32 представлен фазовый портрет в пространстве при параметрическом задании семейства функций [x(t), y(t), z(t)]. 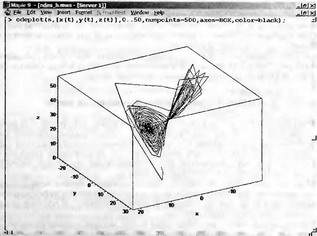 Рис. 7.32. Фазовый портрет колебаний в пространстве Фазовый портрет отчетливо выявляет, что большая часть колебаний развивается в двух плоскостях пространства, причем в каждой из них имеется свой фокус. Еще один вариант пространственного фазового портрета показан на рис. 7.33. Он хорошо представляет динамику развития колебаний в плоскости (у, z) при изменении времени t. Фазовый портрет весьма любопытен — хорошо видны две «трубки» в которых развиваются переходные процессы. В них можно выделить характерные раскручивающиеся спирали. 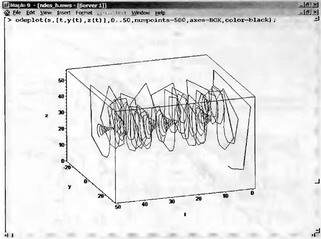 Рис. 7.33. Фазовый портрет колебаний в пространстве [t, y(t), z(t)] Остается отметить, что для повышения наглядности переходных процессов в графиках рис. 7.32 и 7.33 используется вывод осей координат в виде «ящика» (опция axes=BOX) и поворот изображения с помощью мыши. 7.9.4. Распространение волн в нелинейной средеМногие наяву или в кино видели, как большие волны воды в море или океане теряют свой гармонический характер. Их гребни, расположенные в воздухе, явно движется быстрее, чем впадины, в результате во времени гребень достигает предшествующей ему впадины и может даже перегнать ее. Радиотехники давно научились использовать распространение волн в нелинейных средах для получения очень коротких перепадов напряжения или тока. Моделирование этого сложного явления (обострения фронта волн и потеря ими устойчивости) достаточно просто осуществляется волновым дифференциальным уравнением в частных производных Бюргерса. Рисунок 7.34 показывает пример задания и решения этого уравнения. 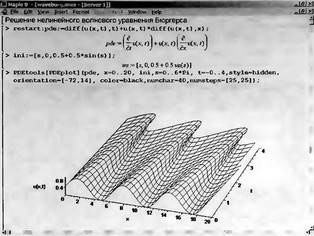 Рис. 7.34. Моделирование процесса распространения волн в нелинейной среде Здесь поначалу задана синусоидальная волна, которая хорошо видна на переднем плане рисунка для малых времен t. Представление результата моделирования в трехмерном пространстве позволяет наглядно представить, как меняется форма волны во времени. Нетрудно заметить, что фронт волны и впрямь обостряется и может даже приобрести отрицательный наклон. 7.10. Интерактивное решение дифференциальных уравнений7.10.1. Новые средства интерактивного решения дифференциальных уравненийПоскольку Maple университетская система, разработчики новых версий Maple предприняли большие усилия в повышении степени визуализации всех стадий решения дифференциальных уравнений. В частности были введены новые средства решения дифференциальных уравнений в интерактивном режиме, при котором каждая стадия решения наглядно отображается в соответствующем окне. Это едва ли нужно инженерам и научным работникам, понимающим суть и стадии решения, но, безусловно, полезно преподавателям и студентам высших учебных заведений. Новые средства решения дифференциальных уравнений представляют собой ряд окон, созданных средствами пакета расширения Maplets. Каждое окно содержит поля для представления уравнений или параметров, там где это надо поля для представления графиков и кнопки управления. Довольно подробное описание процесса интерактивного решения дифференциальных уравнений дано в разделе ODE Analyzer справки. Доступ к нему представлен на рис. 7.35. 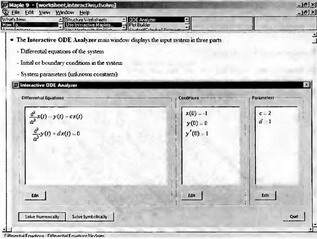 Рис. 7.35. Окно справки по разделу ODE Analyzer 7.10.2. Примеры интерактивного решения дифференциальных уравненийДля интерактивного решения дифференциальных уравнений используется функция dsolve в следующей записи: dsolve[interactive](odesys, options) Здесь указание [interactive] задает вывод первого окна с записью дифференциальных уравнений, представленных параметром odesys и необходимыми опциями options. Примеры применения функции dsolve уже неоднократно приводились. На рис. 7.35 в центре видно окно с записью дифференциальных уравнений, начальных условий для его решения и значениями параметров. Предусмотрено редактирование как самой системы, так и начальных условий и параметров. Для этого достаточно активизировать кнопку Edit в соответствующей части окна. Примеры редактирования можно найти в справке, они просты и наглядны, а потому детали описания редактирования опускаются. Внизу окна имеется две кнопки: Solve Numerically — решение численное; Solve Symbolically — решение символьное (аналитическое). На рис. 7.36 представлен пример численного решения. Для этого случая возможно задание одного из пяти методов решения, задания (если нужно) граничных условий и построение графика решения. 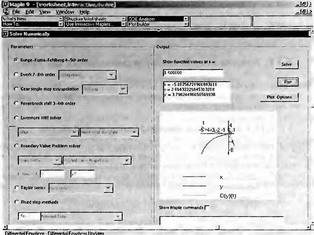 Рис. 7.36. Пример решения системы ОДУ численным методом Другой случай решения — аналитически представлен на рис. 7.37. Решение появляется в подокне при нажатии клавиши Solve. В данном случае оно поместилось в подокне, но если решение слишком громоздко, то активизировав кнопку Large Display можно вывести решение в отдельное большое окно. 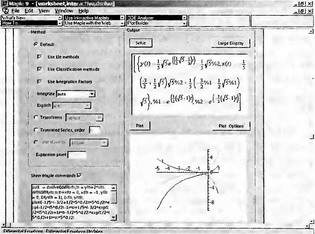 Рис. 7.37. Пример решения системы ОДУ символьным методом Для изменения параметров графиков служит отдельное окно. С его работой и другими деталями интерактивного решения можно познакомиться по справке. 7.11. Анализ линейных функциональных системЗавершим главу описанием пакета LinearFunctionalSystems. Он содержит специальные средства для решения дифференциальных уравнений, описывающих линейные функциональные системы. 7.11.1. Назначение пакета LinearFunctionalSystemsПакет LinearFunctionalSystems содержит набор функций для решения задач, связанных с анализом линейных функциональных систем. Обычно такие системы описываются линейными дифференциальными уравнениями, имеющими то или иное решение. Пакет LinearFunctionalSystems позволяет провести тестирование подготовленной системы, оценить ряд ее параметров и получить решение одним из ряда методов. Вызов всех функций пакета осуществляется командой: > with(LinearFunctionalSystems);[AreSameSolution, CanonicalSystem, ExtendSeries, HomogeneousSystem, IsSolution, MatrixTriangularization, PolynomialSolution, Properties, Rational Solution, SeriesSolution, UniversalDenominator] 7.11.2. Тестовые функции пакета LinearFunctionalSystemsПрежде чем рассматривать основные функции пакета, рассмотрим две тестовые функции. Они представлены следующими формами записи: IsSolution(sol, sys, vars) IsSolution(sol, A, b, x, case) IsSolution(sol, A, x, case) AreSameSolution(sol, sol1) В них: sol — тестируемое решение, sys — система функциональных уравнений, x — независимая переменная решения, А и b — матрица и вектор с рациональными элементами, case — имя метода решения ('differential', 'difference' или 'qdifference') 7.11.3. Функции решения линейных функциональных системГруппа основных функций пакета LinearFunctionalSystems имеет идентичный синтаксис и записывается в виде: name(sys,vars,[method]) или name(A[,b],x,case,[method]) Здесь name — одно из следующих имен: • PolynomialSolution — решение в форме полинома; • RationalSolution — решение в форме рационального выражения; • SeriesSolution — решение в виде ряда; • UniversalDenominator — решение с универсальным знаменателем (и числителем, равным 1). Система функциональных уравнений задается либо в виде полной системы sys со списком переменных vars, либо в матричном виде с заданием матрицы коэффициентов системы А и вектора свободных членов b (может отсутствовать) с указанием независимой переменной x и параметра case, имеющего значения 'differential', 'difference' или 'qdifference'. Параметр method, задающий метод EG-исклю-чения может иметь значения 'quasimodular' или 'ordinary'. 7.11.4. Вспомогательные функцииНесколько вспомогательных функций пакета LinearFunctionalSystems представлено ниже: • MatrixTriangularization(mat, m, n, х, It) — триангуляция матрицы mat размера m×n с указанием типа It ('lead' или 'trail'); • CanonicalSystem(shift, sys, vars) или CanonicalSystem(shift, A[, b], x, case) — возвращает систему в каноническом виде (параметр shift задается как 'difference' или 'q-difference', назначение других параметров соответствует указанным выше для других функций); • ExtendSeries(sol, deg) — расширяет ряд решения sol до расширенного ряда степени deg; • HomogeneousSystem(homo, sys, vars) или HomogeneousSystem(homo, A[, b], x, case) — преобразует исходную систему в гомогенную с именем homo. • Properties(sys, vars) или Properties(A[, b], x, case) — возвращает основные свойства системы. Ряд примеров применения пакета LinearFunctionalSystems представлен в файле lfs и в справке по данному пакету. 7.12. Новые возможности Maple 10 в решении дифференциальных уравнений7.12.1. Средства Maple 10 для аналитического решения дифференциальных уравненийВозможности Maple 10 в решении дифференциальных уравнений существенно расширены. Это прежде всего касается решения ряда таких уравнений в аналитическом виде. В частности введен ряд новых опций для функции dsolve, представляющих решения дифференциальных уравнений, например Абеля, Риккати и др. На рис. 7.38 представлен пример решения линейного дифференциального уравнения, представленного через новую специальную функцию Хеуна (Heun). Этот пример описан в самоучителе Maple 10. 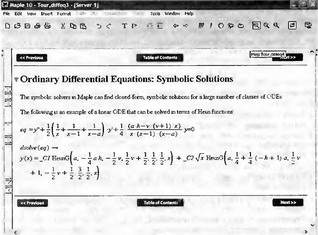 Рис. 7.38. Пример решения линейного дифференциального уравнения Решатель дифференциальных уравнений Maple 10 способен находить аналитические решения и для большого числа дифференциальных уравнений в частных производных. Пример такого решения из самоучителя Maple 10 представлен на рис. 7.39. 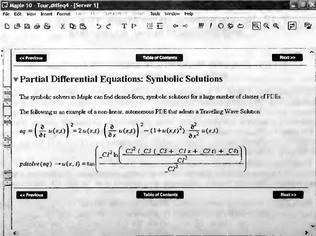 Рис. 7.39. Пример решения дифференциального уравнения в частных производных Поскольку большая часть новых возможностей Maple 10 в решении дифференциальных уравнений представляет ограниченный интерес для большинства пользователей системой Maple 10 подробное их описание едва ли целесообразно Обзор таких функций и решаемых дифференциальных уравнений можно найти в подразделе Differential Equations раздела What's New справки. 7.12.2. Средства Maple 10 численного решения дифференциальных уравненийВ части средств численного решения дифференциальных уравнении повышена надежность решения жестких систем дифференциальных уравнении и дифференциальных уравнений в частных производных. На рис. 7.40 показан пример решения такого уравнения с выводом результатов в виде анимационного двумерного графика и трехмерного графика, представляющего множество решений в разные моменты времени. 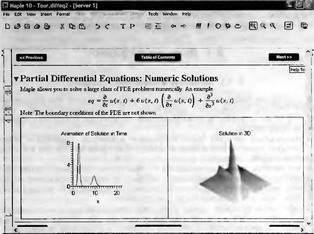 Рис. 7.40. Пример численного решения дифференциального уравнения в частных производных |
|
||
| Главная | В избранное | Наш E-MAIL | Добавить материал | Нашёл ошибку | Наверх | ||||
|
|
||||

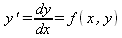 (7.1)
(7.1)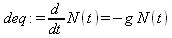
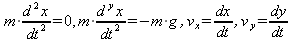 (7.2)
(7.2)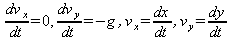 (7.3)
(7.3)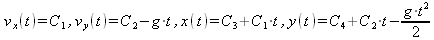 (7.4)
(7.4)