Как мы уже упоминали, создателем теории сравнений был немецкий математик Карл Фридрих Гаусс. Его знаменитая работа по теории чисел «Арифметические исследования» появилась в 1801 году, когда ему было 24 года. В первых главах этой книги рассказывается о теории сравнений. Однако здесь следует упомянуть, что следы теории сравнений можно обнаружить за несколько столетий до Гаусса. Некоторые из них присутствуют в древних правилах проверки арифметических вычислений. Они составляют существенную часть инструкции по арифметическим операциям эпохи Ренессанса. Некоторые из них используются до сих пор, а из всего того, что нам известно об их происхождении, можно сказать, что их корни лежат в античности.

Мы не знаем, каким образом эти правила были впервые введены, однако попытаемся указать один из возможных путей, на котором они могли быть открыты. Вернемся к временам счетных досок. На таком абаке каждая цифра в числах, которые участвовали в вычислениях, обычно выкладывалась с помощью фишек, камней, палочек или орехов, причем каждая группа отмечала количество единиц, десятков, сотен и т. д. в соответствии с местом их нахождения. В нашей десятичной системе число

N = a_n10ⁿ + a_n-110^n-1 +… + a₂10² + a₁10 + a₀ = (a_n, a_n-1…, a₂, a₁, a₀)₁₀ (8.1.1)

потребовало бы для своей записи

S_N = a_n + a_n-1 +… + а₂ + а₁ + а₀ (8.1.2)

фишек. Это число мы называем суммой цифр числа N.

Теперь предположим, что мы хотим выполнить на доске простое действие, а именно: сложить два числа N и M. Тогда мы должны отметить на доске также второе число

M = (b_m, b_m-1, …, b₂, b₁, b₀)₁₀,

у которого на тех же линиях лежит

S_M = b_m + b_m-1 + … + b₂ + b₁ + b₀

складываемых фишек. На некоторых линиях может теперь лежать больше, чем по 9 фишек. Операция, необходимая для нахождения числа N + М, состоит в замене десяти фишек на одной линии одной фишкой на следующей линии. И так нужно продолжать до тех пор, пока такой процесс возможен. На каждом шаге заменяют десять фишек одной-единственной и таким образом происходит потеря девяти фишек на доске. Итак, мы видим, что если сложение выполнено правильно, то число фишек, остающихся на доске, должно удовлетворять условию

S_N+M ≡ S_N + S_M (mod 9), (8.1.3)

т. е. количество фишек, находящихся на доске, должно отличаться от первоначального общего числа фишек на число, кратное 9. Эта проверка (8.1.3) до сих пор сохранила свое старое название «выбрасывание девяток».

После того как это правило было открыто, не составило труда заметить, что оно также применимо при сложении нескольких чисел, при вычитании и при умножении; в последнем случае, в соответствии с (8.1.3),

S_M S_N ≡ S_MN (mod 9). (8.1.4)

Теоретическое доказательство этих правил является легкой задачей при использовании сравнений. Очевидно, что

1 ≡ 1, 10 ≡ 1, 10² ≡ 1, 10³ ≡ 1… (mod 9); (8.1.5)

таким образом, из (8.1.1) и (8.1.2) мы делаем вывод, что

N ≡ S_N (mod 9).    (8.1.6)

Поэтому из правил сравнений, которые мы установили в § 3 главы 7, ясно, что

S_N ± S_M ≡ N ± М ≡ S_{N ± M},

S_N • S_M = N •M ≡ S_N•M (mod 9).

Правило «выбрасывания девяток» чаще всего применяется к умножению. Возьмем в качестве примера числа

M = 3119, N = 3724 (8.1.7)

и их произведение

М • N = 11 614 156.

Это вычисление не может быть верным, так как если бы оно было верным, то мы имели бы, что

M ≡ S_M ≡ 3 + 1 + 1 + 9 ≡ 5 (mod 9),

N ≡ S_N ≡ 3 + 7 + 2 + 4 ≡ 7(mod 9)

и MN ≡ S_MN ≡ 1 + 1 + 6 + 1 + 4 + 1 +5 + 6 ≡ 7 (mod 9).

Но 5 • 7 = 35 ≠ 7 (mod 9).

В действительности же это произведение равно MN = 11 615 156.

В средневековых школах ученики имели строгий наказ обязательно проводить проверку своих упражнений. Поэтому в рукописях, сохранившихся с тех времен, мы видим множество знаков, похожих на эмблему из скрещенных костей. Такой знак для нашего примера выглядит так, как на рис. 18.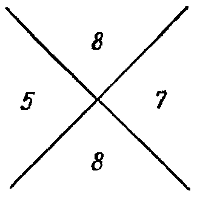

Рис. 18.

Здесь числа 5 и 7, лежащие слева и справа, означают остатки чисел М и N (по модулю 9), а верхнее число 8 является остатком вычисленного произведения MN. Оно должно проверяться с помощью произведения остатков начальных чисел, записываемого в нижней части.

Здесь

5 • 7 = 35 ≡ 8 (mod 9).

Рис. 19.

Такая проверка «скрещенных костей» была совершенно обычной в ранних изданиях учебников арифметики (рис. 19), например, в английских учебниках семнадцатого и восемнадцатого веков. Конечно, существует возможность, что вычисления содержат ошибку, необнаруживаемую методом «выбрасывания девяток», но тогда мы знаем, что ошибка является «ошибкой по модулю 9».

Ясно, что и при другом основании системы счисления можно использовать простейшую проверку. Для числа

M = m_nbⁿ + m_n-1b^n-1 +… + m₂b² + m₁b + m₀,

записанного при основании b, как и в (8.1.5), мы имеем

1 ≡ 1, b ≡ 1, b² ≡ 1… (mod (b — 1));

поэтому, как и раньше,

М ≡ S_M = m_n + m_n-1 +… + m₂ + m₁ + m₀ (mod (b — 1)),

и проверочное правило остается прежним.

Это, по-видимому, совершенно тривиальное замечание применимо даже в нашей обычной десятичной системе. Мы упоминали в § 5 главы 7, что если мы разобьем цифры десятичного числа на группы по три, то тогда эта группировка может рассматриваться как представление числа при основании b = 10³ = 1000. Аналогично, если группировать цифры в пары, то это соответствует представлению числа при основании b = 10² = 100.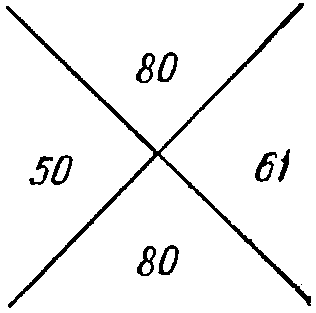

Рис. 20.

Взяв числа 3119 и 3724 вновь в качестве примера и записав

M = 31 19, N = 37 24, MN = 11 61 51 56,

мы находим

M ≡ 31 + 19 = 50 (mod 99), N ≡ 37 + 24 = 61 (mod 99),

MN ≡ 11 +61+ 51+56 = 179 ≡ 80 (mod 99).

Здесь наша проверка «скрещенных костей» будет такой, как на рис. 20, потому что, как легко видеть, 50 • 61 ≡ 80 (mod 99).

Эта проверка более эффективна, чем «выкидывание девяток», потому что модули в этом случае гораздо больше и вероятность, что ответ будет правильным, соответственно гораздо больше. Другими словами, «ошибка по модулю 99» менее вероятна, чем «ошибка по модулю 9».

Многие задачи астрономии и хронологии, связанные с периодичностью, могут быть сформулированы в терминах теоретико-числовых понятий. Возьмем простой пример: определение дня недели, который падает на заданный день. Дни недели повторяются с периодом 7, поэтому вместо обычных названий мы можем дать каждому дню номер:

воскресенье = 0,

понедельник = 1,

вторник     = 2,

среда       = 3,

четверг     = 4,

пятница     = 5,

суббота     = 6.

Если мы это сделаем, то каждому целому числу соответствует день недели, а именно: день, определяемый его остатком по модулю 7.

Если бы мы имели благоприятнейшую ситуацию, при которой количество дней в году делилось на 7, то все даты падали бы на одни и те же дни ежегодно, и составление расписаний было бы гораздо проще, а издатели календарей имели бы меньше работы. Однако количество дней в году равно

365 ≡ 1 (mod 7),

за исключением високосных лет, в которых количество дней

366 ≡ 2 (mod 7).

Это показывает, что для обычного года номер W дня недели заданной даты в следующем году увеличится на 1, например, если в этом году 1 января — воскресенье, то в следующем году он будет падать на понедельник. Это не слишком сложно, однако, эта простая схема нарушается високосными годами. Это происходит каждый четвертый год, тогда номер дня недели увеличивается на 2. Более того, возникает дополнительная трудность из-за того, что добавочный день високосного года прибавляется не в начале или конце года, а 29 февраля. Поэтому, для удобства, в общей формуле для вычисления W, которую мы дадим ниже, договоримся считать март — первым месяцем, апрель — вторым и т. д., при этом январь будет одиннадцатым месяцем, а февраль — двенадцатым месяцем предшествующего года.

Но на этом наши трудности не кончаются. В юлианском календаре, введенном по указу Юлия Цезаря, было принято, что год точно равен 365 1/4 дня, в соответствии с правилом високосного года. Однако это не совсем правильно, так как астрономический год в действительности равен 365,2422 дня.

Эта маленькая ошибка вызвала постепенный сдвиг сезонов по отношению к календарю, например, в шестнадцатом веке день весеннего равноденствия (первый день весны) пал на 11 марта вместо 21 марта, как это должно было быть.

Чтобы исправить положение, в 1582 году папа Григорий XIII после долгих колебаний произвел реформу календаря в странах с католическим вероисповеданием. В том году было опущено 10 дней, а именно, пятницу 5 октября стали считать пятницей 15 октября. Более того, для корректирования календаря были введены следующие григорианские правила для високосных лет.

Годы столетий

1700, 1800, 1900, 2100, 2200, 2300…,

в которых количество столетий не делится на 4, не считаются високосными годами. Оставшиеся годы столетий

1600, 2000, 2400…

продолжают считаться високосными годами. Получается очень хорошее приближение к правильной длине года, однако капельку длиннее. Было предложено не считать годы 4000, 8000… високосными вопреки григорианскому правилу; но так как этот вопрос еще открыт и не имеет отношения к ближайшему будущему, то мы не будем это принимать в нашей формуле.

Предположим теперь, что нам задана дата: d-й день в m-м месяце (где m определяется так, как было указано выше), в году, равном

N = c • 100 + Y, (8.2.1)

где с—количество столетий, а Y — номер года в столетии. Тогда можно доказать, что наш номер дня недели определяется при помощи сравнения

W ≡ d + [1/5 (13m -1)] + Y + [1/4 Y] + [1/4 c] — 2с (mod 7). (8.2.2)

Квадратные скобки, фигурирующие в этой формуле, были введены в § 3 главы 4 для обозначения наибольшего целого числа, не превосходящего числа, стоящего внутри этих скобок.

Пример. День Пирл-Харбора[12], 7 декабря 1941 г. Здесь

d = 7, m = 10, с = 19, Y = 41,

так что

W = 7 + 25 + 41 + 10 + 4 — 38 ≡ 0 (mod 7).

т. е. это было в воскресенье.

Пример. Каким днем недели будет 1 января 2000 года? Здесь

d = 1, m = 11, с = 19, Y = 99

и

W = 1 + 28 + 1 + 3 + 4 — 38 ≡ 6 (mod 7);

таким образом, первый день следующего столетия[13] будет субботой.

При пользовании этой формулой следует помнить, что ее нельзя применять для того периода, когда еще не был введен григорианский календарь. В Англии и английских колониях он был введен в 1752 году, при этом из календаря было опущено одиннадцать дней: 3 сентября стали считать 14 сентября по новому стилю[14].

Оставшаяся часть этого параграфа предназначена для тех, кто хотел бы познакомиться с выводом формулы (8.2.2). Вывод формулы проведем в два этапа. Во-первых, определим номер дня недели для 1 марта произвольного N-го года в формуле (8.2.1). Начнем отсчет от некоторого года, скажем, от 1600-го, и обозначим номер дня недели для 1 марта этого года через d₁₆₀₀. Можно было бы узнать номер этого дня из архивных документов, но можно обойтись и без этого, а получить его, как результат рассуждений.

Если бы не было високосных лет, то мы могли бы найти d_N — номер дня недели 1 марта N-то года, просто добавляя по одному дню к d₁₆₀₀ для каждого из прошедших лет. Это дает число

d₁₆₀₀ + (100с + Y — 1600) (mod 7). (8.2.3)

Принимая во внимание високосные годы и предполагая, что они следуют регулярно каждый четвертый год, мы должны прибавить к первому выражению еще следующее:

[1/4 (100с + Y — 1600)] = 25с — 400 + [1/4 Y]. (8.2.4)

Однако это чуть больше, чем нужно, потому что год окончания каждого столетия обычно не бывает високосным, и ввиду этого мы должны вычесть число

с—16. (8.2.5)

Но мы должны еще учесть следующее исключение: если с — номер столетия, делится на четыре, то год 100 с считается високосным. Таким образом, нужно добавить последнюю поправку

[1/4 (с -16)] = [1/4 с] — 4. (8.2.6)

Теперь мы сложим выражение (8.2.3) и (8.2.4), вычтем (8.2.5) и прибавим (8.2.6). Это даст нам номер дня недели 1 марта N-гo года в виде выражения

d_N ≡ d₁₆₀₀ + 124с + Y — 1988 + [1/4 с] + [1/4 Y] (mod 7).

Чтобы упростить его, мы приводим числа по модулю 7 и таким образом получаем

d_N ≡ d₁₆₀₀ — 2с + Y + [1/4 с] + [1/4 Y] (mod 7). (8.2.7)

Применим эту формулу к 1968 году, в котором 1 марта падает на пятницу, следовательно, d₁₉₆₈ = 5.

Здесь с = 19, [1/4 c] = 4, Y = 68, [1/4 Y] = 17,

и мы находим d₁₉₆₈ = 5 ≡ d + 2 (mod 7).

Это даст нам, что d₁₆₀₀ = 3, следовательно, 1 марта 1600 года было средой. Когда мы вставим полученное значение в (8.2.7). мы придем к формуле

d_N = 3 — 2с + Y + [1/4 с] + [1/4 Y] (mod 7) (8.2.8)

для номера дня недели 1 марта N-го года.

Вторым этапом будет определение количества дней по модулю 7 от 1 марта до произвольно взятого дня этого года. Так как количество дней в месяце

меняется, то для этого требуется некоторая хитрость. Начнем с нахождения количества дней, которые нужно прибавить к номеру дня 1 марта, чтобы получить номер дня 1 числа любого другого месяца по модулю 7.

Так как в марте 31 день, то для получения номера 1 апреля нужно добавить 3, для получения номера 1 мая мы должны добавить 3 + 2 дней, так как в апреле 30 дней. Продолжая рассмотрение для последующих месяцев, мы получаем добавочные слагаемые в виде следующей таблицы:

В качестве другого простого применения теории сравнений можно рассмотреть составление расписаний соревнований, проходящих по круговой системе, подобных тем, которые составляются во всех видах соревнований от шахмат до футбола.

Обозначим количество участников (или команд) через N. Если число N — нечетное, то в каждом туре соревнований невозможно разбить все команды на пары — каждый раз одна из команд будет свободна от игры. Мы можем обойти эту трудность, добавив фиктивную команду T₀ и составляя расписание для (N + 1)-й команды, включая команду Т₀. В каждом туре команда, которой выпадает играть с командой Т₀, будет свободна от игры.

Из сказанного следует, что можно считать количество команд N четным числом. Каждой команде мы сопоставим число

х = 1, 2…, N—1, N.

Общее количество туров, которое должна сыграть каждая команда, равно N — 1.

Предположим теперь, что х принадлежит множеству {1, 2…, N-1}. (8.3.1)

В качестве противника команды х в r-м туре мы назначим команду с номером у, из множества (8.3.1), где число y_r удовлетворяет сравнению

x + y_r ≡ r (mod (N — 1)). (8.3.2)

Чтобы увидеть, что при этом разные команды х имеют разных противников, заметим, что сравнение

x + y_r ≡ r ≡ x' + y_r (mod (N — 1))

означает, что

x ≡ x' (mod (N — 1))

или х = x', так как эти числа принадлежат множеству (8.3.1).

Единственная сложность возникает в том случае, когда х = y_r, и таким образом в формуле (8.3.2) получаем

2x ≡ r (mod (N — 1)). (8.3.3)

Существует лишь одно значение х во множестве (8.3.1), для которого выполняется это соотношение. Действительно, если

2x ≡ r ≡ 2x' (mod (N — 1)),

то отсюда следует, что

2(x — x') ≡ 0 (mod (N — 1)),

или

х = х' (mod (N — 1)),

так как N — 1 — нечетное число. Решение сравнения (8.3.3) на множестве (8.3.1) всегда существует, а именно:

x = r/2, если r — четное,

x = (r + N — 1) / 2, если r—нечетное.

С помощью соотношения (8.3.2) мы приписали в r-м туре для каждой команды х ее противника, за исключением номера х₀, который удовлетворяет условию (8.3.3). Команда х₀ в этом туре будет встречаться с командой, имеющей номер N.

Осталось показать, что в результате такого подбора любая команда в каждом туре r = 1, 2…, N играет с различным противником. Сначала мы удостоверимся в этом для команды с номером N, имеющей в некотором смысле особое положение. В r-м туре она играет с командой х₀, определяемой из соотношения (8.3.3). Предположим, что s ≠ r; тогда в s-м туре N-я команда играет с командой, имеющей номер x'₀, удовлетворяющий соотношению

2x'₀ ≡ s (mod (N — 1)).

При этом не может случиться, что х₀ = х', так как это привело бы к тому, что

2х₀ = 2х'₀ ≡ r ≡ s (mod (N — 1))

и, следовательно, r = s.

Теперь рассмотрим различных противников команды х, принадлежащей множеству (8.3.1). С командой, имеющей номер N, эта команда играет только один раз, а именно в туре r₀, где r₀ определяется из сравнения

2x ≡ r₀ (mod(N — 1)).

Предположим теперь, что r ≠ r₀ и s ≠ r₀. Тогда противники команды х в r-м и s-м турах будут определяться из соотношения (8.3.2):

х + у_r ≡ r (mod (N—1)) и х + y_s = s (mod (N —1)). Вновь из равенства y_r = y_s будет следовать r = s, откуда мы делаем вывод, что y_r ≠ y_s.

Построим таблицу соревнований, проходящих по круговой системе, для N = 6 команд с помощью изложенного метода. Проведя несколько простых вычислений, получим приведенную ниже таблицу. На пересечении r-й строки и x-го столбца стоит номер того противника команды с номером х, с которым она играет в r-м туре.

r \ х 1 2 3 4 5 6

 1    5 4 6 2 1 3

 2    6 5 4 3 2 1

 3    2 1 5 6 3 4

 4    3 6 1 5 4 2

 5    4 3 2 1 6 5

Система задач 8.3.

1. Постройте таблицу для N = 8 игроков.

2. Покажите, что когда r = 2, команды 1, 2…, N встречаются с командами N, N — 1…, 2, 1 соответственно.

3. Почему команда с номером N—1 в r-м туре играет всегда с r-й командой, за исключением r = N—1? С какой командой она играет в этом исключительном случае?

4. Убедитесь, что если в соответствии с формулой команда х в r-м туре играет с командой у, то команда у в этом туре играет с командой х.

В заключение обсудим применение сравнений в качестве метода определения того, является ли некоторое большое число простым или составным. Этот очень эффективный метод особенно хорош, когда речь идет о некотором числе, выбранном наугад. Он основан на малой теореме Ферма (7.5.8).

Пусть N — исследуемое число. Выберем небольшое число а взаимно простое с N. Удобно в качестве числа а брать некоторое небольшое простое число, не являющееся делителем числа N, например, 2, 3 или 5. Если бы N было простым числом, то для него было бы справедливо сравнение

а^N-1 ≡ 1 (mod N), (8.4.1)

в соответствии с малой теоремой Ферма. Следовательно, если мы проверим это сравнение (8.4.1) и убедимся, что оно не выполняется, то можно утверждать, что число N является составным.

Пример. Возьмем N = 91 и выберем а = 2. Тогда

a^N-1 = 2⁹⁰ = 2⁶⁴ • 2¹⁶ • 2⁸ • 2²

Более того,

2⁸ = 256 ≡ -17 (mod 91),

2¹⁶ = (2⁸)² ≡ (-17)² = 289 ≡ 16 (mod 91),

2³² = (2¹⁶)² ≡ (16)² = 256 ≡ -17 (mod 91),

2⁶⁴ = (2³²)² ≡ (-17)² = 289 ≡ 16 (mod 91),

так что

2⁹⁰ = 2⁶⁴ • 2¹⁶ • 2⁸ • 2² ≡ 16 • 16 • (-17) • 4 ≡ 64 ≠ 1 (mod 91).

Отсюда делаем вывод, что число N составное. И действительно, 91 = 7 • 13.

Наш пример слишком прост, чтобы на нем увидеть действительную силу метода. Составив соответствующую программу для ЭВМ, можно таким способом установить, что некоторые очень большие числа являются составными. К сожалению, этот метод не указывает на то, какие именно множители имеет данное число, следовательно, во многих случаях мы знаем, что число составное, однако не имеем представления о его делителях.

В особенности это относится к числам Ферма

F_n = 2^2ⁿ+1,

которые мы обсуждали в § 3 главы 2. Как мы уже отмечали, они являются простыми для n = 0, 1, 2, 3, 4. Чтобы проверить число

F₅ = 2^2ˆ5 + 1 = 2³² + 1 = 4294967297

с помощью теоремы Ферма, можно взять а = 3. Если бы F₅ было простым числом, мы бы имели, что

З^2ˆ32 ≡ 1 (mod F₅). (8.4.2)

Чтобы вычислить остаток степени в левой части сравнения, мы должны возвести число 3 в квадрат 32 раза и всякий раз привести полученный результат по модулю F₅. Мы избавим читателя от подробностей. Можно найти, что сравнение (8.4.2) не выполняется, следовательно, число F₅ является составным. Известный множитель 641 был найден путем проб. Тот же самый метод был использован для того, чтобы показать, что несколько больших чисел Ферма не являются простыми. Для некоторых из них нам известны множители, а для других нет.

Если сравнение (8.4.1) выполняется для некоторого числа а, взаимно простого с числом N, то число N может как быть простым, так и не быть им. При этом случаи, когда сравнение выполняется для составного числа N, являются исключительными, поэтому при выполнении сравнения мы можем быть почти уверены в том, что число N — просто. Однако для многих целей хотелось бы знать наверняка, является ли данное число простым. Это удается сделать с помощью усовершенствованного метода, основанного на следующем замечании: N является простым числом в том случае, если сравнение (8.4.1) выполняется для степени N — 1, но не выполняется ни для какой степени, являющейся делителем числа N — 1.

Имеется другой подход, эффективный для не слишком больших чисел N. Возьмем а = 2. Американские математики Пуль и Лемер нашли с помощью ЭВМ все значения чисел N ≤ 100 000, исключительные в том смысле, что выполняется сравнение

2^N-1 ≡ 1 (mod N), (8.4.3)

но число N является составным. Такие числа N иногда называют псевдопростыми. Для каждого из этих чисел N были указаны также наибольшие простые множители.

С помощью таблиц Пуля и Лемера можно определить простоту любого числа N ^ 100 000 000. Сначала проверяется выполнимость сравнения (8.4.3). Если это сравнение не выполняется, то число N — составное. Если же это сравнение выполняется и число N есть в таблицах, то оно также составное, и мы можем прочесть в таблицах его простой множитель. И наконец, если сравнение (8.4.3) выполняется и числа N нет в таблицах, то оно простое.

Наименьшим составным числом, удовлетворяющим сравнению (8.4.3), является

N = 341 = 11 • 31.

В пределах 1000 существуют еще два таких числа,

а именно:

N = 561= 3 • 11 • 17,

N = 645 = 3 • 5 • 43.

Число 561 является замечательным, так как соответствующее сравнение (8.4.1) выполняется для каждого целого числа а, взаимно простого с числом N. Мы называем такие особые числа числами, имеющими свойство Ферма. По таким числам в последнее время было проведено огромное количество исследований.

Примечания:

1

Игра с передвижением фишек по размеченной доске. (Прим. перев.)

12

День нападения японского флота на американскую военную базу Пирл-Харбор, начало войны США и Японии. (Прим. перев.)

13

Это распространенная ошибка. Первым днем следующего столетия будет 1 января 2001 года, который будет понедельником. (Прим. перев.)

14

У нас переход на григорианский календарь произошел в 1918 году; вместо 1 февраля старого стиля стали считать 14 февраля нового стиля. (Прим. перев.)