Во введении (§ 3, гл. 1) мы упоминали об одной из древнейших теоретико-числовых задач: найти все прямоугольные треугольники с целочисленными сторонами, т. е. найти все целочисленные решения уравнения

х² + y² = z². (5.1.1)

Эта задача может быть решена с использованием лишь простейших свойств чисел. Прежде чем приступить к ее решению, проведем некоторые предварительные исследования. Тройка целых чисел

(х, у, z), (5.1.2)

удовлетворяющая уравнению (5.1.1), называется пифагоровой тройкой. Отбросим тривиальный случай, когда одна из сторон треугольника равна нулю.

Ясно, что если множество (5.1.2) является пифагоровой тройкой, то любая тройка чисел

(kx, ky, kz), (5.1.3)

получающаяся умножением каждого из этих чисел на некоторое целое число k, также будет пифагоровой, и наоборот. Таким образом, при поиске решений достаточно ограничиться нахождением простейших треугольников, длины сторон которых не имеют общего множителя k > 1. Например, тройки

(6, 8, 10), (15, 20, 25)

являются пифагоровыми тройками, получающимися из простейшего решения (3, 4, 5).

В простейшей тройке (x, у, z) не существует общего множителя для всех трех чисел. В действительности справедливо более сильное утверждение: никакие два числа из простейшей тройки не имеют общего множителя, т. е.

D(x, y) = 1, D(x, z) = 1, D(y, z) = 1. (5.1.4)

Чтобы доказать это, предположим, что, например, х и у имеют общий делитель. Тогда они имеют общий простой делитель р. В соответствии с (5.1.1) число р должно также делить и r. Итак, (х, у, z) не может быть простейшей тройкой. Такие же рассуждения применимы для доказательства остальных двух утверждений.

Рассмотрим еще ряд свойств простейших троек. Мы только что получили, что числа х и у не могут быть оба четными, но мы можем также показать, что они не могут быть и оба нечетными. Действительно, предположим, что

x = 2a +1, y = 2b + 1.

После возведения в квадрат этих чисел и сложения их, получим число

x² + y² = (2a + 1)² + (2b + 1)² = 2 + 4а + 4a² + 4b + 4b² = 2 + 4 (а + а² + b + b²),

делящееся на 2, но не делящееся на 4. В соответствии с (5.1.1) это означает, что z² делится на 2, но не делится на 4, но это невозможно, так как если z² делится на 2, то и z делится на 2, но тогда z² делится на 4.

Так как одно из чисел х и у — четное, а другое — нечетное, то z — также нечетное. Для определенности будем считать, что в наших обозначениях число х — четное, а у — нечетное.

Чтобы найти простейшие решения уравнения Пифагора (5.1.1), перепишем его в виде

x² = z² — y² = (z + y)(z — y). (5.2.1)

Вспоминая, что х — четное, а у и z — оба нечетные, получаем, что все три числа

х, z + y, z — y

четные. Тогда мы можем разделить обе части уравнения (5.2.1) на 4 и получить

(1/2 x)² = 1/2 (z + y) 1/2 (z — y). (5.2.2)

Обозначим

m₁ = 1/2 (z + y), n₁ = 1/2 (z — y); (5.2.3)

тогда уравнение (5.2.2) перепишется как

(1/2 x)² = m₁n₁. (5.2.4)

Числа m₁ и n₁ взаимно простые. Чтобы это увидеть, предположим, что

d = D(m₁, n₁)

есть наибольший общий делитель чисел m₁ и n₁. Тогда, как это следует из § 1 гл. 4, число d должно делить оба числа

m₁ + n₁ = z, m₁ — n₁ = y.

Но единственным общим делителем чисел z и у в простейшей тройке может быть только 1, поэтому

d = D(m₁, n₁) = 1. (5.2.5)

Так как произведение (5.2.4) этих двух взаимно простых чисел является квадратом, то можно использовать результат, изложенный в конце § 2 гл. 4 (стр. 50), согласно которому числа m₁ и n₁ являются квадратами

m₁ = m², n₁ =, D(m, n) = 1. (5.2.6)

Здесь мы можем без нарушения общности считать, что m > 0, n > 0. Теперь подставим m² и n² вместо m₁ и n₁ соответственно в уравнения (5.2.3) и (5.2.4);

получим

m² = 1/2 z + 1/2 y, n² = 1/2 z — 1/2 y, m²n² = 1/4 x²,

т. е.

x = 2mn, y = m² — n², z = m² + n². (5.2.7)

Проверка показывает, что эти три числа всегда удовлетворяют соотношению Пифагора х² + у² = z².

Осталось определить, какие целые положительные числа m и n в действительности соответствуют простейшим треугольникам. Докажем, что следующие три условия на числа m и n являются необходимыми и достаточными:

(1) (m, n) = 1,

(2) m > n, (5.2.8)

(3) одно из чисел m и n четное, а другое — нечетное.

Доказательство. Сначала покажем, что если числа х, у, z образуют простейшую тройку, то условия (5.2.8) выполняются. Мы уже показали, что условие (1) является следствием того, что числа х, у, z взаимно простые. Условие (2) следует из того, что числа х, у, z — положительны. Чтобы увидеть, что условие (3) необходимо, заметим, что если m и n оба нечетные, то в соответствии с (5.2.7) у и z были бы оба четные, в противоречие с результатами, полученными в конце предыдущего параграфа.

Наоборот, если условия (5.2.8) выполнены, то соотношения (5.2.7) определяют простейшую тройку: условие (2) обеспечивает положительность чисел х, у и z.

Могут ли какие-нибудь два из этих трех чисел иметь общий простой множитель р? Такое простое число р, делящее два из них, должно также делить и третье в силу соотношения х² + у² = z². Если число р делит х, то оно в соответствии с (5.2.7) должно делить 2mn. Число р не может равняться 2, потому что у и z нечетные в соответствии с условием (3) и (5.2.7). Предположим, что р ≠ 2 — нечетное простое число, делящее m. Тогда условие (1) и выражение (5.2.7) показывают, что р не может делить у и z. Такие же рассуждения применимы и для случая, если р делит число n.

Найдя необходимые и достаточные условия (5.2.8) для того, чтобы m и n давали простейший треугольник, можно вычислить все такие треугольники с помощью соотношения (5.2.7). Например, пусть

m = 11, n = 8.

Наши условия выполнены, и мы находим, что

х = 176, у = 57, z = 185.

В табл. 3 приведены все простейшие треугольники х, у, z для нескольких первых значений чисел т и n.

Таблица 3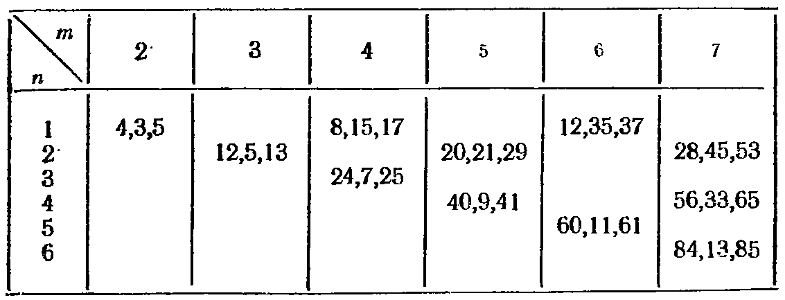

Система задач 5.2.

1. Продлите таблицу для всех значений m ≤ 10.

2. Могут ли два разных набора значений чисел m и п, удовлетворяющих условию (5.2.8), дать один и тот же треугольник?

3. Найдите все пифагоровы треугольники, у которых длина гипотенузы не превосходит 100.

Мы решили задачу нахождения всех треугольников Пифагора. Здесь, как почти всегда в математике, решение одной задачи приводит к постановке ряда других задач. Часто новые вопросы оказываются значительно более трудными, чем первоначальный.

Одним из естественных вопросов о простейших треугольниках является следующий. Пусть задана одна из сторон простейшего треугольника Пифагора, как найти остальные? Первым рассмотрим случай, когда известна сторона у. В соответствии с (5.2.7)

y = m² — n² = (m + n)(m — п), (5.3.1)

где m и n—числа, удовлетворяющие условиям (5.2.8).

В уравнении (5.3.1) множители (m + n) и (m — n) взаимно простые. Чтобы в этом убедиться, заметим, что эти множители

а = m + n, b = m — n (5.3.2)

оба нечетные, так как одно из чисел m и n нечетное, а другое четное. Если числа а и b имеют общий нечетный простой множитель р, то число р должно было бы делить каждое из чисел

а + b = m + n + (m — n) = 2m

и

а — b = m + n — (m — n) = 2n,

т. е. р должно было бы делить числа m и n. Но это невозможно, так как D(m, n) = 1.

Предположим теперь, что есть разложение данного нечетного числа у на два множителя

y = a  b, a > b, D(a, b) = 1. (5.3.3)

Из (5.3.2) получаем

m = 1/2 (a + b), n = 1/2 (a — b). (5.3.4)

Эти два числа также взаимно простые, поскольку любой их общий множитель должен был бы делить числа а = m + n и b = m — n. Кроме того, числа m и n не могут быть оба нечетными, ибо тогда каждое из чисел а и b делилось бы на 2. Отсюда заключаем, что числа m и n удовлетворяют условиям (5.2.8) и, таким образом, определяют простейший треугольник, одна из сторон которого у = m² — n².

Пример. Пусть y = 15. Для него существуют два разложения на множители, удовлетворяющие условиям (5.3.3), а именно:

у = 15 • 1 = 5 • 3.

Первое из них дает

m = 8, n = 7, x = 112, у = 15, z = 113,

а второе

m = 4, n = 1, x = 8, y = 15, z = 17.

Пусть, далее, задана сторона х. Так как какое-то из чисел m или n делится на 2, то очевидно, что х = 2mn должно делиться на 4. Если разложить число х/2 на два взаимно простых множителя, то больший из них можно взять в качестве числа m, а меньший — n.

Пример. Возьмем х = 24; тогда

1/2 x = 12 • 1 = 4 • 3.

Первое разложение дает

m = 12, n = 4, х = 24, y = 143, z = 145,

а второе

т = 4, n = 3, х = 24, у = 7, z = 25.

Третий и последний случай приводит нас к необходимости коснуться одной важной задачи теории чисел. Если z — гипотенуза простейшего треугольника Пифагора, то в соответствии с (5.2.7) имеем

z = m² + n². (5.3.5)

т. е. число z есть сумма квадратов чисел m и n, удовлетворяющих условиям (5.2.8).

Это приводит нас к постановке вопроса, уже решенного П. Ферма: когда целое число можно представить в виде суммы квадратов двух целых чисел:

z = a² + b²? (5.3.6)

На время забудем все ограничения на числа а и b. Пусть они могут иметь общие множители, а также каждое из них, или даже сразу оба могут обращаться в нуль. Перечислим все целые числа, меньшие десяти, представляемые в виде суммы двух квадратов:

0 = 0² + 0², 1 = 1² + 0², 2 = 1² + 1², 4 = 2² + 0², 5 = 2² + 1², 8 = 2² + 2², 9 = 3² + 0², 10 = 3²+1².

Оставшиеся числа 3, 6 и 7 не представляются в виде суммы двух квадратов.

Опишем, как можно выяснить, является ли число суммой двух квадратов. К сожалению, мы не можем привести здесь доказательства ввиду его сложности.

Рассмотрим вначале простые числа. Каждое простое число вида р = 4n + 1 всегда является суммой двух квадратов; например,

5 = 2² + 1², 13 = 3² + 2², 17 = 4²+1², 29 = 5² + 2².

Существенно, что такое представление может осуществляться единственным способом.

Остальные нечетные простые числа имеют вид q = 4n + 3, т. е.

q = 3, 7, 11, 19, 23, 31…

Ни одно такое простое число не представляется в виде суммы двух квадратов; более того, вообще ни одно число вида 4n + 3 не может быть представлено в виде суммы двух квадратов. Чтобы убедиться в этом, заметим, что если целые числа а и b оба четные, то а² и b² оба делятся на 4, отсюда и а² + b² делится на 4. Если они оба нечетные, например, а = 2k + 1, b = 2l + 1, то а² + b² = 4k² + 4k + 1 + 4l² + 4l + 1 = 4 (k² + l² + k + l) + 2, поэтому а² + b² имеет при делении на 4 остаток 2. И наконец, если одно из целых чисел а и b четное, а другое — нечетное, скажем, а = 2k + 1, b = 2l, то а² + b² = 4k² + 4k + 1 + 4l² и имеет при делении на 4 остаток 1. Итак, мы перебрали все возможности и можем заключить, что сумма двух квадратов никогда не представима в виде 4n + 3.

Чтобы закончить наше исследование для простых чисел, заметим, что 2 = 1² + 1².

Для того чтобы проверить, является ли составное число z суммой двух квадратов, разложим его на простые множители

z = p₁^α₁ p₂^α₂ •… • p_k^α_k. (5.3.7)

Число z оказывается суммой двух квадратов тогда и только тогда, когда каждое простое число p_i вида 4п + 3 входит в разложение в четной степени.

Примеры. Число z = 198 = 2 • З² • 11 не является суммой двух квадратов, так как 11 имеет вид 4n + 3 и входит в разложение в первой степени.

Число z = 194 = 2 • 97 является суммой двух квадратов, так как ни один из его простых множителей не является числом вида 4n + 3. Действительно, z = 13² +5².

Вернемся к нашей первоначальной задаче нахождения всех чисел z, которые могут быть гипотенузами простейших треугольников Пифагора. Такое число z должно быть представимо в виде z = m² + n², где числа m и n удовлетворяют условиям (5.2.8). Необходимым и достаточным условием для этого является следующее: каждый из простых множителей числа z должен иметь вид 4n + 1. Доказательство этого утверждения мы вновь опускаем.

Примеры. z = 41. Это число легко представить в виде суммы двух квадратов искомого вида, z = 5² + 42, так что m = 5, n = 4 и x = 40, у = 9, z = 41 выражают длины сторон соответствующего треугольника.

z = 1105 = 5 • 13 • 17. Существуют четыре представления этого числа в виде суммы двух квадратов:

1105 = ЗЗ² + 4² = 32² + 9² = 31² + 12² = 24² + 23².

Стороны соответствующих треугольников вычислите самостоятельно.

Целый ряд задач о треугольниках Пифагора может быть решен при помощи наших формул (5.2.7)

х = 2mn, у = m² — n², z = m² + n².

Например, можно искать треугольники Пифагора с заданной площадью А. Если такой треугольник является простейшим, то его площадь равна

А = 1/2 ху = mn (m — n) (m + n). (5.3.8)

Здесь три из четырех множителей нечетны. Нетрудно видеть, что они попарно взаимно простые. Поэтому, чтобы найти все возможные значения чисел m и n, можно выделить из числа А два взаимно простых нечетных множителя k и k (k > l), положив

m + n = k, m — n = l,

что дает

m = 1/2 (k + l), n = 1/2 (k — l).

После этого мы проверяем, удовлетворяют ли эти числа условиям (5.3.8).

Рассуждения несколько упрощаются, если заметить, что два множителя в выражении (5.3.8) могут равняться 1 только в единственном случае:

m = 2, n = 1, A = 6.

Действительно, два множителя в (5.3.8) могут быть равны 1, только если

n = m — n = 1,

что и дает указанное выше значение.

Пример. Найдем все треугольники Пифагора с площадью А = 360. Разложение числа А на простые множители таково: A = 2³  3² • 5. Число А может быть единственным образом записано в виде произведения четырех взаимно простых множителей: А = 8 • 1 • 5 • 9. Если мы ищем простейший треугольник, то m + n = 9. Однако если m = 8, то n = 1 и m — n = 7, но А не делится на 7, а вторая возможность (n = 8, m = 1) исключается условием > n. Поэтому такого треугольника не существует.

Этот результат не исключает возможности существования треугольников с площадью А = 360, не являющихся простейшими. Следующее соображение может быть использовано в общем случае для нахождения треугольников заданной площади, не являющихся простейшими. Если длины всех сторон треугольника имеют общий делитель d, т. е. могут быть записаны как

dx, dy, dz,

то его площадь равна

А = 1/2 dx dy = d²mn (m — n) (m + n).

Таким образом, число d² является множителем числа А и, если число d есть наибольший общий делитель длин сторон, то число

А₀ = A/d² = mn (m — n) (m + n)

должно быть площадью простейшего треугольника.

Применим полученный результат к только что рассмотренному случаю А = 360. У этого числа существуют три множителя, являющиеся квадратами;

d₁ = 4, d₂ = 9, d₃ = 36.

Соответственно находим

A/d₁ =90 = 2 • 3² • 5, A/d₂ = 40 = 2³ • 5, A/d₃ = 10 = 2 • 5.

Не существует способов написать число 40 или 10 в виде произведения четырех взаимно простых множителей, а число 90 может быть представлено в таком виде, причем единственным образом, а именно:

90 = 1 • 2 • З² • 5.

(В числе сомножителей 1 может встречаться не более одного раза, за исключением случая m = 2, n = 1, А = 6.) Так как наибольшим множителем является 9, то мы должны взять m + n = 9. Однако, перебирая все возможные значения m = 1, 2, 5, получим соответственно n = 8, 7, 4. Условие m > n исключает все случаи, кроме m = 5, n = 4, для которого, однако, mn (m + n) (m — n) ≠ 90. Итак, мы получили, что не существует ни простейшего, ни иного треугольника Пифагора с площадью А = 360.

Можно было бы затронуть еще много других вопросов, но упомянем лишь об одном из них. Периметр треугольника равен

c = x + y + z; (5.3.9)

для простейшего треугольника Пифагора получаем

с = 2mn + (т² — n²) + (m² + n²) = 2n (m + n).

Мы предоставляем читателю самому отыскать метод нахождения всех треугольников Пифагора с заданным периметром. Не пренебрегайте рассмотрением

числовых примеров.

Мы решили задачу построения всех треугольников Пифагора. Это ведет нас к исследованию более общих связанных с ней задач. Естественным обобщением задачи Пифагора является задача Герона, названная по имени древнегреческого математика Герона, жившего в Александрии: найти все треугольники с целочисленными сторонами, площади которых также выражаются целыми числами. Эта задача отличается от задачи Пифагора тем, что условие наличия прямого угла заменено требованием целочисленности площади. Очевидно, что всякий треугольник Пифагора удовлетворяет условиям задачи Герона.

Для проверки того, является ли данный треугольник треугольником Герона, проще всего применить формулу Герона для площади треугольника,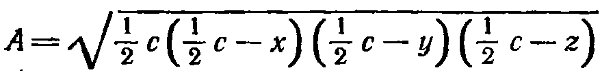

где с — это периметр треугольника, определенный в (5.3.9). Хотя известно значительное число треугольников Герона, не существует общей формулы, описывающей все эти треугольники. Приведем несколько из них (не прямоугольных):

x = 7 y = 15 z = 20

    9     10     17

   13     14     15

   39     41     50

Мы не можем закончить рассказ о треугольниках Пифагора, не упомянув об одной из самых знаменитых проблем математики, гипотезе П. Ферма:

для n > 2 не существует натуральных чисел x, у, z таких, что

хⁿ + уⁿ = zⁿ.

Эта идея пришла к Ферма в то время, когда он изучал перевод с греческого «Арифметики» Диофанта. В этой книге в основном рассматриваются задачи, в решении которых применяются формулы для нахождения треугольников Пифагора. Читая эту книгу, Ферма делал пометки на нолях.

Ферма был взволнован своим «открытием», он верил, что у него есть удивительное доказательство, и сожалел, что не может его записать, так как поля слишком узки. С тех пор эта задача занимает математиков. Для нахождения доказательства изобретались самые искусные методы; этот поиск привел к открытию новых фундаментальных теорий в математике. Используя теоретические разработки и вычисления на ЭВМ, было показано, что теорема Ферма справедлива для многих значений степени n. В настоящее время мы знаем, что этот результат выполняется для всех значений n, удовлетворяющих неравенству 3 ≤ n ≤ 4002.

Попытки самых выдающихся математиков в течение столетий найти общее доказательство оказались тщетными. Поэтому распространилось мнение, что Ферма, несмотря на свой бесспорный талант, стал жертвой самообмана. Как бы ни широки были поля книги, маловероятно, что его доказательство было бы верным.

Конечно, вы имеете право попробовать свои силы в доказательстве этой теоремы, но предупреждаем, что еще ни одна теорема в математике не имела столько неправильных доказательств, как теорема Ферма. Лишь некоторые из них принадлежат хорошим математикам, остальные — дилетантам. Доказательства «последней теоремы Ферма» продолжают появляться в почте известных математиков, занимающихся теорией чисел. Большинство из этих доказательств сопровождается письмами с требованием о немедленном всемирном признании и выплате денежной премии, установленной одним немецким математиком (эта премия давно уже обесценилась в результате инфляции).

Система задач 5.3.

1. Найдите все такие треугольники Пифагора, у которых длина одной из сторон равна: а) 50, б) 22.

2. Используя условие представимости числа в виде суммы двух квадратов, определите, какие из чисел 100, 101…, 110 могут быть представлены в таком виде. Если возможно, найдите все представления. Какое из этих чисел может быть гипотенузой простейшего треугольника Пифагора?

3. Могут ли быть треугольниками Пифагора треугольники с площадями А = 78, A = 120, А = 1000?

4. Найдите все треугольники Пифагора с периметрами с = 88, с = 110.