«Все есть число» — учили древние пифагорейцы[8]. Однако количество чисел, которыми они пользовались, ничтожно по сравнению с фантастической пляской цифр, окружающих нас сегодня в повседневной жизни. Огромные числа появляются, когда считаем мы, и тогда, когда считают нас. В нашу жизнь прочно вошли: номера домов, квартир, телефонов, счетов, почтовые индексы. Каждый день наполнен потоком счетов, чеков и других бухгалтерских документов. Государственный бюджет исчисляется в миллиардах, а горы статистических данных являются принятым доводом в спорах. Эти цифры «крутятся» в компьютерах, которые анализируют состояние производства, следят за траекториями спутников и исследуют атомные ядра со скоростью до одного миллиарда операций в секунду.

Ко всему этому вела длинная дорога, начавшаяся с первых попыток человека систематизировать окружающие его числа, когда они стали столь большими, что их нельзя уже было посчитать на пальцах. Были перепробованы различные способы группировки чисел; большинство из них осталось на обочине этого пути, не выдержав конкуренции с другими системами. К настоящему времени, по счастью, наша десятеричная, или десятичная, система счисления, основанная на группировании десятками, принята почти всюду; в некотором отношении эта система, по-видимому, случайно, оказалась той золотой серединой, которая одинаково хорошо удовлетворяет разнообразным требованиям при работе с числами.

Нет необходимости подробно описывать эту систему. Первые два года обучения в школе дают нам на всю жизнь почти подсознательное знание того, что означает последовательность цифр, например,

75 = 7 • 10 + 5,

1066 = 1 • 10³ + 0 • 10² + 6 • 10 + 6,

1970 = 1 • 10³ + 9 • 10² + 7 • 10 + 0.

И вообще, в системе, основанной на числе 10,

_________________

а_n а_n-1 … a₂ а₁ a₀

означает число

N = a_n • 10ⁿ + a_n-1•10^n-1 +….. + a₂ • 10² + a₁ • 10 + a₀, (6.1.2)

где коэффициенты, или цифры, а_i могут принимать следующие значения:

а_i = {0, 1…. 9}. (6.1.3)

Число b = 10 называется основанием этой системы. Индо-арабская числовая система пришла в Европу с Востока около 1200 г. нашей эры, и с тех пор не оспаривалась. Она известна как позиционная система, так как место каждой цифры определяет ее значение; использование символа 0 дает возможность просто и безболезненно обозначать пустующее место. Более того, оказалось, что эта система очень удобна при арифметических операциях с числами: сложении, вычитании, умножении и делении.

Известны различные другие системы, которыми пользовались народы мира, чтобы навести порядок среди чисел. Но почему и как возникли эти системы? Ответы на эти вопросы большей частью затерялись в туманном прошлом человечества.

Никто не сомневается, что широко используемая группировка десятками объясняется тем, что люди считали на пальцах. Довольно странно, что сохранилось мало свидетельств того, что человек считал на одной руке; пятеричная система встречается исключительно редко. Но в то же время очень часто встречаются примеры двадцатеричной системы. Не нужно иметь семи пядей во лбу, чтобы понять, что в этой системе в процессе счета участвуют пальцы как рук, так и ног. Из этих двадцатеричных систем счисления, возможно, самая известная — система племени майя, но и в Европе такие системы были широко распространены несколько столетий назад. Двадцатеричная система прослеживается во французском языке в числах от 80 до 100, что можно увидеть из следующих примеров:

80 = quatre-vingts = четыре раза по двадцать,

90 = quatre-vingts-dix = четыре раза по двадцать и десять

91 = quatre-vingts-onze = четыре раза по двадцать и одиннадцать

и так далее.

Менее известно, что в датском языке счет парами десятков процветает вплоть до наших дней. Эта древняя система, которая ранее была широко распространена среди германских племен, столь оригинальна, что мы не можем не привести хотя бы несколько ее деталей.

При счете до 20 естественно использовать такие термины, как:

tredsindstyve = три раза по двадцать,

firsindstyve = четыре раза по двадцать,

femsindstyve = пять раз по двадцать.

Но система становится более сложной, если условиться, что всякий раз, когда мы просчитаем несколько полных двадцаток, а затем еще десяток, объявлять, что находимся на половине следующей двадцатки; например,

90 = halvfemsindstyve = половина пятой двадцатки.

Чтобы закончить наше описание, следует сказать, что в датском языке количество единиц ставится перед количеством десятков, что приводит к числовым конструкциям типа

93 = treoghalvfemsindstyve = три и половина пятой двадцатки.

Ясно, что в любой цивилизации, насыщенной числами, подобно нашей, такие системы обречены. Способ записи чисел, при котором единицы ставятся перед десятками, особенно неприятен. Такая система была также распространена в Англии до XVIII века: вместо twenty-three (двадцать три) обычно говорили three and twenty (три и двадцать). В Норвегии лишь несколько лет назад парламент специальным законом отменил использование такой системы в школах и всех официальных сообщениях. Однако подобная система продолжает процветать в Германии, что приводит к многочисленным числовым ошибкам, например, при набирании номера телефона.

С давних времен до наших дней астрономы пользуются древней вавилонской шестидесятеричной системой (с основанием 60). Правда, сейчас ее достоинства уменьшились, но мы все же придерживаемся этой системы при отсчете времени и углов в минутах и секундах. Мы не знаем, почему вавилоняне ввели столь большое основание в свою систему, можно лишь предположить, что эта система возникла как комбинация двух систем с различными основаниями, скажем, 10 и 12, у которых наименьшее общее кратное равно 60.

Теперь скажем несколько слов о математических вопросах, связанных с использованием систем с различными основаниями. При основании b мы записываем целое число

N = c_nbⁿ + c_n-1b^n-1 +… + с₂b² + с₁b + с₀  (6.2.1)

так же, как и в (6.1.2), с той разницей, что здесь коэффициенты с, могут принимать значения

с_i = 0, 1…, b — 1, (6.2.2)

вместо значений, приведенных в (6.1.3). Для краткости можно записать число N из (6.2.1) в сокращенной форме

(с_n, с_n-1…, с₂, с₁, с₀)_b, (6.2.3)

соответствующей записи (6.1.1), при этом в записи (6.2.3) необходимо приписать используемый базис — число b, чтобы избежать путаницы.

Примеры. В шестидесятеричной системе (3, 11,43)₆₀ = 3 • 60² + 11 • 60 + 43 = 11 503.

В системе с основанием b = 4 (3, 2, 0, 1) = 3 • 4³ + 2 • 4² + 0 • 4 + 1 = 225.

Вообще, когда число задано в системе с основанием b, мы находим это число в обычной десятичной системе, вычисляя значения степеней числа b, умножая каждое из них на соответствующую цифру и складывая, как уже делалось в вышеприведенных примерах.

Теперь рассмотрим обратную задачу. Задается число N и мы хотим представить его при основании b. Мы можем сделать это повторным делением на b. Взгляните на формулу (6.2.1). Можно записать ее в виде

N = (cⁿb^n-1 +… + c₂b + c₁) b + c₀.

Так как с₀ меньше, чем b, то с₀ является остатком при делении числа N на b. Мы можем записать это деление

N = q₁b + c₀, q₁ = c_nb^n-1 +… + c₂b + c₁,

для того чтобы показать, что c₁ получается делением числа q₁ на b тем же способом, и т. д. Таким образом мы находим коэффициенты с_i в результате серии делений на число b:

N = q₁b + c₀,

q₁ = q₂b + с₁,

……

q_n-1 = q_nb + с_n-1,

q_n = 0 b + с_n,

при этом мы продолжаем деление до тех пор, пока не окажутся выполненными соотношения q_n < b, q_n+1 = 0. Мы приводим два примера, которые помогут вам понять этот процесс.

Пример 1. Выразим число 101 при основании 3. Мы выполняем деление на 3, как указывалось выше, и находим

101 = 33 • 3 + 2,

33 = 11 • 3 + 0,

11 = 3 • 3 + 2,

3 = 1 • 3 + 0,

1 = 0 • 3 + 1.

Отсюда

101 =(1, 0, 2, 0, 2)₃.

Пример 2. Выразим число 1970 при основании 12. Здесь деление на 12 таково:

1970 = 164 • 12 + 2,

164 = 13 • 12 + 8,

13 = 1 • 12 + 1,

1 = 0 • 12 + 1.

Следовательно,

1970 = (1, 1, 8, 2)₁₂.

Система задач 6.2.

1. Выразите числа (1, 2, 3, 4)₅, (1, 1, 1, 1, 1, 1)₃ в десятичной системе.

2. Представьте числа 362, 1969, 10 000 при основаниях b = 2; 6; 17.

Американское общество сторонников двенадцатеричной системы предложило изменить нашу десятеричную систему на более эффективную и удобную, как они думают, систему с основанием 12. Те, кто предлагает эту систему, указывают, что было бы выгоднее иметь систему с основанием, делящимся на числа 2, 3, 4 и 6, так как процесс деления на эти часто встречающиеся делители упрощается. Доводы такого типа привели бы нас к шестидесятеричной системе, основание которой, число 60, делится на числа

2, 3, 4, 5, 6, 10, 12, 15, 20, 30.

В ряде стран многие вещи все еще считают дюжинами и гроссами (т. е. дюжинами дюжин) и естественно, что для них двенадцатеричная система является вполне возможной. Для перехода в двенадцатеричную систему нужно было бы ввести двенадцать новых символов, что потребует для их разработки столь же много усилий, сколько потребовалось для создания десятеричной системы. Некоторые энтузиасты считают, что необходимо ввести новые символы лишь для 10 и 11, но такой способ не учитывает неудобств, возникающих в период перехода: никто не будет понимать, например, означает ли запись 325

3 • 10² + 2 • 10 + 5 = 325

или

3 • 12² + 2 • 12 + 5 = 461.

Для того чтобы получить представление о том, как меняется количество знаков в числе в зависимости от системы счисления, возьмем число

10ⁿ — 1 = 99… 9 (n раз) = N (6.3.1)

в десятеричной системе. Это самое большое число с n знаками. Чтобы найти m — количество знаков при записи этого числа при основании b — мы должны определить m как целое число, для которого выполняются неравенства

b^m > 10ⁿ — 1 ≥ b^m-1. (6.3.2)

Это условие может быть также записано в виде

b^m ≥ 10ⁿ > b^m-1.

Возьмем логарифмы этих трех чисел. Вспомнив, что lg 10 = 1, получим, что

m lg b ≥ n > (m — 1) lg b.

В свою очередь эти неравенства могут быть переписаны в виде

m ≥ n/lg b > (m — 1); (6.3.3)

таким образом, m является первым целым числом не меньшим, чем n/lg b.

Отсюда делаем вывод, что, грубо говоря, m — новое количество знаков, может быть получено делением числа n на lg b.

Примеры. Пусть вновь n будет количеством знаков числа в десятичной системе. Для b = 2 мы имеем: lg 2 = 0,30103, таким образом, количество цифр в двоичной системе приблизительно равно 3,32 n. Когда b = 60, мы имеем: lg 60 = 1,778, отсюда количество знаков приблизительно равно 0,56 n, т. е. немного больше, чем половина количества знаков в десятичной системе.

Ясно, что короткими числами удобнее оперировать. Но, с другой стороны, числа при больших основаниях имеют ряд недостатков. Во-первых, нужно иметь названия и обозначения для b различных цифр, чего обычно нет для больших значений b. Например, в вавилонской шестидесятеричной системе считали единицы до 60, группируя их по десять, как показано на рис. 15.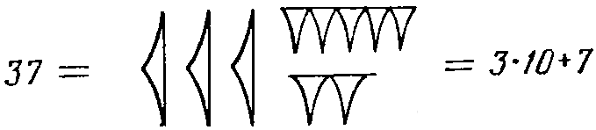

Рис. 15.

Это означает в действительности, что эта система расщеплялась на подсистемы с десятеричной записью. Аналогичная ситуация существует в двадцатеричной системе народа майя. Здесь цифры до 20 считались пятерками, как показано на рис. 16.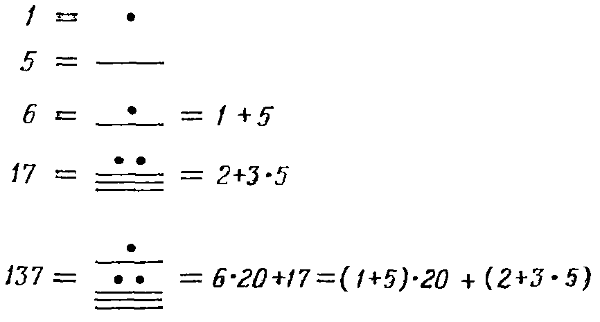

Рис. 16.

Вторым и гораздо большим недостатком является трудность, возникающая при попытках вычислений с помощью обычных методов. Когда мы выполняем действие умножения, то пользуемся знанием наизусть таблицы умножения, т. е. знанием произведений всех десяти цифр. Эта таблица Пифагора, как ее называют во многих странах, вдалбливалась нам в течение первых школьных лет, и знаем мы ее почти автоматически. Это знание не столь тривиально, как мы склонны думать. Из средневековых арифметических манускриптов ясно видно, что умножение было на грани высшей математики, а деление больших чисел было в действительности редким искусством. Но можно привести и гораздо более поздние примеры.

Самюэль Пепис, известный благодаря своему дневнику, был в возрасте около тридцати лет и служил клерком канцелярии лорда-хранителя печати, когда летом 1662 года он решил, что он должен знать кое-что из математики, по крайней мере основы арифметики, чтобы самостоятельно проверять счета. Заметим, что он тогда уже получил степени бакалавра и магистра в Кембридже. В то время было довольно обычным, что хорошо образованный английский джентльмен совершенно не владеет повседневными расчетами; эти расчеты могли перепоручаться младшим счетоводам.

4 июля 1662 года Пепис записывает в своем дневнике: «Вскоре придет мистер Купер, помощник капитана на „Ройял Чарльз", у которого я собираюсь учиться математике, и сегодня мы начнем; он очень способный человек, я полагаю, что не найдется дела, которое способно полностью его удовлетворить. После часа занятий арифметикой (я пытался выучить таблицу умножения) мы расстались с ним до завтра».

Каждый день и рано утром и поздно вечером Пепис учил проклятую таблицу умножения, с трудом продвигаясь вперед при поддержке своего моряка-учителя. Например, 9 июля он записывает: «Встал в четыре часа утра и снова упорно учу таблицу умножения, которая для меня является главной трудностью арифметики». Так продолжалось несколько дней, пока 11 июля он смог записать: «Встал в четыре часа утра и упорно работал над таблицей умножения, которой я теперь почти овладел». Пепис хорошо использовал полученные с таким трудом знания во всех все более важных постах, на которые он назначался. Однако может показаться слишком быстрым его продвижение, когда вы узнаете, что он был избран членом знаменитой Британской академии наук — Королевского общества — спустя два с половиной года после того, как выучил таблицу умножения.

Мы привели эту историю, которая никоим образом не является уникальной, чтобы подчеркнуть: запоминание таблицы умножения в те дни не было обычным этапом математического знания. Таким образом, мы видим, что использование в нашей арифметике чисел с небольшим основанием дает ряд преимуществ, как механических, так и интеллектуальных. Например, когда основанием является число b = 3, то в таблице умножения

  | 0 1 2

  |________ 

0 | 0 0 0

1 | 0 1 2

2 | 0 2 (1,1)₃

существует только единственное нетривиальное умножение, а именно: 2 • 2 = 4 = (1, 1)₃.

Для b = 2 мы имеем совершенно тривиальную таблицу

  | 0 1

  |____

0 | 0 0

1 | 0 1

Система задач 6.3.

1. Доказать, что количество нетривиальных умножений цифр (получающееся отбрасыванием умножений на 0 и 1) в системе с основанием b равно 1/2 (b — 1) (b — 2).

2. Чему равна сумма всех элементов в таблице умножения? Проверьте для b = 10.

Обсудим несколько задач, связанных с системами счисления, которые имеют отношение к выбору оснований систем счисления, удобных для машинного счета. Предположим, что мы имеем дело с обычным настольным арифмометром, который работает при помощи сцепленных числовых колес, каждое из которых имеет 10 цифр: 0, 1, … 9. Если имеется n колес, то мы можем представить все числа вплоть до

N = 99…9 (n раз), (6.4.1)

как и в (6.3.1).

Предположим теперь, что в качестве основания мы взяли число b, отличное от 10, но продолжаем рассматривать числа до N. Тогда мы должны иметь m колес, где m — целое число, удовлетворяющее условиям (6.3.2) и (6.3.3). Как и в (6.3.4). число m является целым числом, равным числу n/lg b или следующим за ним. Так как каждое колесо несет b цифр, то количество цифр, записанных на колесах, приближенно равно

D = n  b/lg b.

Можно теперь спросить: какое нужно выбрать число b, чтобы получить наименьшее количество чисел, записанных на колесах? Чтобы найти наименьшее значение числа D, в формуле (6.4.2) необходимо лишь исследовать функцию

f(b) = b/lg b (6.4.3)

для различных оснований b = 2, 3, 4… С помощью таблицы логарифмов получаем значения

 b    2    3    4    5    6

f(b) 6,64 6,29 6,64 7,15 7,71

Последующие значения для f(b) еще больше; например, f(10) = 10, как уже отмечалось. Мы заключаем, что для таких арифмометров имеет место следующее утверждение.

Наименьшее общее число цифр на арифмометре достигается при b = 3.

Видно, что для b = 2 и b = 4 общее число цифр не на много больше; в этом смысле маленькие основания имеют преимущество.

Рассмотрим небольшое изменение этой задачи. Обычные счеты того типа, который иногда используется для обучения детей счету, имеют несколько металлических спиц с девятью[9] подвижными косточками на каждой из них, чтобы отмечать цифры чисел. С таким же успехом можно провести параллельные прямые на листе бумаги и отмечать цифры соответствующим количеством спичек, или же подобно древним начертить эти прямые на песке и отмечать цифры камешками.

Но вернемся к счетам. Если имеется n спиц и на каждой по 9 косточек, то можно представить вновь все целые числа с п знаками вплоть до числа N, записанного в (6.4.1). Теперь зададим следующий вопрос: можно ли, взяв другое основание b, сделать счеты более компактными, т. е. обойтись меньшим количеством косточек?

При основании b количество косточек на каждой спице будет b — 1. Как и прежде, для того чтобы счеты имели ту же вместимость N, количество знаков или спиц должно определяться соотношением (6.3.4). Это дает значение

E = n/lg b  (b — 1) (6.4.4)

в качестве приближения для общего количества косточек. Чтобы найти, когда это число принимает наименьшее возможное значение, мы должны исследовать функцию

g(b) = (b — 1)/lg b (6.4.5)

для различных значений числа b = 2, 3… Значение функции g(b) для небольших значений числа b даны в таблице

  b   2    3    4    5    6

g(b) 3,32 4,19 4,98 5,72 6,43

Для больших значений числа b функция продолжает возрастать, поэтому мы заключаем, что необходимое количество косточек на счетах будет минимально при b = 2.

Можно интерпретировать этот результат с другой точки зрения. Предположим, что мы отметили цифры нашего числа, используя спички или камешки, расположенные на прямых линиях. В десятичной системе будет от 0 до 9 отметок на каждой прямой. Это дает в среднем по 4,5 спички на каждой прямой для наугад взятых чисел; следовательно, числа с n знаками потребуют в среднем 4,5 n спичек, когда они укладываются произвольно.

Посмотрим, какое время потребуется, чтобы уложить эти спички на места. Имея в виду какое-нибудь расположение, предположим, что потребуется одна секунда, чтобы уложить одну спичку. Тогда общее время, требуемое для того, чтобы уложить все спички, будет в среднем составлять приблизительно 4,5 n секунд.

Предположим, что мы изменили наше основание на число b и допустим ту же самую вместимость для представления чисел. В таком случае на каждой прямой будет от 0 до b — 1 спичек, следовательно, в среднем 1/2 (b — 1) из всего количества спичек. Как мы упоминали несколько раз, мы будем иметь приблизительно n/lg b прямых. Отсюда делаем вывод, что среднее время, требуемое для представления числа с n знаками, составляет примерно

n/lg n  1/2 • (b — 1) = 1/2 E

секунд, здесь Е есть выражение из (6.4.4). Так как это время было минимальным для b = 2, мы также можем сделать вывод:

среднее время, необходимое для установления числа с помощью спичек на прямых, минимально для b = 2.

Система задач 6.4.

1. Постройте графики функций y = f(b) из (6.4.3) и у = g(b) из (6.4.5) для b > 1. Если вы уже знакомы с дифференциальным исчислением, используйте его для определения формы кривых.

До появления электронных вычислительных машин всюду при вычислениях безраздельно господствовала десятичная система. Интерес к другим системам носил либо исторический, либо познавательный характер. Существовало лишь несколько отдельных задач, которые наиболее удачно формулировались с использованием двоичной или троичной систем счисления. Одним из излюбленных примеров в книгах по теории чисел является игра «Ним»[10]. К тому времени, когда появилось много различных типов компьютеров, возникла задача сделать устройство ЭВМ как можно более компактным и эффективным. Это привело к тщательному изучению систем счисления с целью нахождения более подходящей системы. По ряду причин, некоторые из которых мы обсудили в предыдущем параграфе, двоичная система была признана предпочтительной. Единственным ее недостатком явилось то, что для большинства из нас требуются немалые усилия для того, чтобы чувствовать себя в ней «как дома», так как мы были воспитаны в других традициях. Следовательно, поскольку числа, которые должны вводиться в компьютеры, обычно записаны в десятичной системе, то требуется начальное устройство, переводящее их в двоичную систему, а ответы в конце концов должны быть выражены в десятичной системе, как уступка менее математически подготовленным членам общества.

Разумеется, двоичная система, используемая в ЭВМ, является той же самой системой, которую мы обсуждали в предыдущем параграфе, однако используемая терминология носит более технический оттенок. Двоичные цифры 0, 1 называются битами, что является сокращением английского выражения Binary digiTs (двоичные цифры). Так как существуют лишь две возможности: 0 и 1 в каждой позиции, то часто говорят об элементе с двумя состояниями.

Если следовать общему правилу, изложенному в § 2 этой главы, то представление данного числа в двоичной системе довольно просто. Например, возьмем N = 1971. Повторное деление на b = 2 дает

1971 = 985 • 2 + 1,

985 = 492 • 2 + 1,

492 = 246 • 2 + 0,

246 = 123 • 2 + 0,

123 = 61 • 2 + 1,

61 = 30 • 2 + 1,

30 = 15 • 2 + 0,

15 = 7 • 2 + 1,

7 = 3 • 2 + 1,

3 = 1 • 2 + 1,

1 = 0 • 2 + 1,

Следовательно,

1971₁₀ = (1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1)₂.

Ранее мы отмечали, что в двоичной системе числа имеют более длинные выражения, следовательно, становится труднее с первого взгляда оценить величину числа. По этой причине в языке ЭВМ часто используется восьмеричная система счисления (с основанием 8). Это является лишь незначительным изменением двоичной системы, которое получается разбиением бит в числе на группы по три. Это можно представить себе как систему с основанием

b = 8 = 2³.

Коэффициентами при этом являются восемь чисел

0 = 000, 4 = 100, 1 = 001, 5 = 101, 2 = 010, 6 = 110, 3 = 011, 7 = 111.

В качестве иллюстрации возьмем число 1971 из рассмотренного выше примера; в восьмеричной системе оно представляется как

1971 = 011, 110, 110, 011 = (3, 6, 6, 3)₈.

Таким образом, этот способ записи незначительно отличается от предыдущего. В действительности, такое деление на группы нам хорошо знакомо по обычным десятичным числам: при записи и произнесении большого числа мы обычно делим его цифры на группы по три, например,

N = 89 747 321 924.

Таким образом, можно сказать, что это является представлением нашего числа при основании b = 1000= 10³.

В компьютерах иногда используются и другие представления чисел. Предположим, что мы хотим записать десятичное число, скажем, N = 2947, в ЭВМ, работающей в двоичной системе. Тогда, вместо того чтобы полностью менять N на двоичное число, можно было бы изменить лишь цифры этого числа

2 = 0010,

9 = 1001,

4 = 0100,

7 = 0111

и, таким образом,

N = 0010, 1001, 0100, 0111.

Такие числа известны как кодированные десятичные числа. Этот метод иногда называется «системой 8421», так как эти десятичные цифры представляются в виде сумм двоичных единиц

0 = 0000, 1 = 0001, 2 = 0010,

2² = 4 = 0100, 2³ = 8 = 1000.

Такие кодированные десятичные числа неудобны для всех видов вычислений, но не всегда целью ЭВМ являются вычисления. Тем же образом, любая буква алфавита или любой другой символ могут быть приписаны какому-нибудь двоичному числу. Это означает, что любое слово или предложение можно запоминать как двоичное число. Таким образом, если бы мы были соответствующим образом натренированы и имели бы дело со столь же подготовленной аудиторией, то могли бы общаться лишь с помощью бит.

Система задач 6.5.

1. Найдите двоичное представление чисел Ферма (§ 3, гл. 2)

2. Найдите двоичные представления четных совершенных чисел (§ 4, гл. 3)

Существует множество видов игр с числами, некоторые из которых были известны еще в средние века. Большинство из них не представляет интереса для теории чисел, скорее всего, они подобно магическим квадратам принадлежат к классу кроссвордов с числами. Некоторые из них проиллюстрируем примерами.

Перед вами телеграмма, посланная школьником домой, с настоятельной просьбой:

  S E N D

  M O R E

_________

M O N E Y[11]

Будем рассматривать эту схему, как сложение двух четырехзначных чисел SEND и MORE, в сумме дающих число MONEY. Каждая буква означает определенную цифру. Задача состоит в том, чтобы определить, какие это цифры. Так как всего 10 цифр, то в каждой такой задаче может фигурировать не более 10 букв, в этом примере 8. В идеальном случае задача должна иметь единственное решение.

В нашем примере очевидно, что M = 1, так как М — первая цифра либо суммы S + М, либо S + M+1, где S и М — числа, не превосходящие числа 9. Тогда для числа S имеются две возможности:

S = 9 или S = 8,

так как либо S + 1, либо S + 1 + 1 есть двузначное число. Установим сначала, что S не может быть цифрой 8, ибо, если бы S было 8, то должен был бы быть перенос из колонки сотен, что дает

S + M + 1 = 8 + 1 + 1 = 10

при сложении в колонке сотен. Следовательно, О должно было бы быть нулем и наше послание читалось бы так:

  8 Е N D

  1 0 R Е

_________

1 0 N Е Y

Но, исследуя колонку сотен, находим, что обязательно должен быть перенос из колонки десятков (иначе Е + 0 = Е, а не N), и так как Е ≤ 9, то

E + 0 + 1 = 10.

Это вынудило бы нас положить N = 0, но мы уже знаем, что О = 0, поэтому такой случай невозможен, и мы заключаем, что S = 9, и послание теперь читается так:

  9 Е N D

  1 0 R E 

_________

1 0 N Е Y

Так как Е ≠ N, то сложение в колонке сотен приводит к условию E + 1 = N,

и

  9  Е E+1 D

  1  0  R Е

____________

1 0 E+1 Е Y

Сложение в колонке десятков дает либо

E + 1 + R = 10 + E, либо E + 1 + R + 1 = 10 + E.

Первый случай невозможен, так как он дает R = 9, что противоречит тому, что S = 9. Во втором случае R = 8, и послание читается так:

  9  Е Е+1 D

  1  0  8  E

____________

1 0 E+1 Е  Y

И наконец, сумма в колонке единиц такова:

D + E = 10 + Y.

Для трех букв D, E, Y остаются только значения 2, 3, 4, 5, 6, 7. Наибольшая сумма двух различных чисел из них равна 13. Отсюда существует всего две возможности для Y: либо Y = 2, либо Y = 3. Последний случай невозможен, так как при этом D + E = 13, но мы не можем иметь E = 7, так как тогда N = E + 1 = 8 = R; также не может быть D = 7, так как тогда E = 6 и N = E + 1 = 7 = D.

Таким образом, Y = 2 и D + E = 12. Из имеющихся цифр 2, 3, 4, 5, 6, 7 единственной парой, в сумме дающей 12, являются 5 и 7. Так как Е ≠ 7, то это означает, что D = 7, Е = 5 и, таким образом, единственное решение нашей задачи следующее:

  9 5 6 7

  1 0 8 5

_________

1 0 6 5 2

Этот процесс довольно сложен, во многих случаях можно получить решение гораздо более простым путем.

Система задач 6.6.

1. Попытайтесь проанализировать следующие при-

меры только что показанным методом:

1. S Е N D

   M O R E

   G O L D

 _________

 M O N E Y

2. H O C U S

   P O C U S

 ___________

 P R E S T O

3. F O R T Y

       T E N

       T E N

   _________

   S I X T Y

4. A D A M

     A N D

     E V E

         A

   _______

   R A F T

5. S E E

   S E E

   S E E

   Y E S

 _______

 E A S Y

Переводы этих ребусов таковы:

1. «Шлите больше золотых монет», 2. «Фокус — Покус — Престо», 3. «Сорок + десять + десять = шестьдесят», 4. «Адам и Ева на плоту», 5. «Смотри, смотри, смотри. Да! Легко».

Если хотите, попробуйте придумать свои ребусы. Если вы знакомы с ЭВМ, то попытайтесь запрограммировать решение таких задач.

Примечания:

1

Игра с передвижением фишек по размеченной доске. (Прим. перев.)

8

Последователи философской школы Пифагора. (Прим. перев.)

9

На счетах, принятых в СССР, на каждой спице располагается 10 косточек. (Прим. перев.)

10

При игре в «Ним» раскладывается некоторое количество камешков в несколько кучек. Двое играющих по очереди берут камешки из кучек, при ходе можно брать произвольное количество камней, но только из одной кучки. Выигрывает игрок, взявший последний камень. (Прим. перев.)

11

Вышлите побольше денег.