|
||||
|
|
ГЛАВА 7 СРАВНЕНИЯ § 1. Определение сравнения Теория чисел имеет свою алгебру, известную, как теория сравнений. Обычная алгебра первоначально развивалась как стенография для операций арифметики. Аналогично, сравнения представляют собой символический язык для делимости, основного понятия теории чисел. Понятие сравнения впервые ввел Гаусс. Прежде чем мы обратимся к понятию сравнения, сделаем одно замечание о числах, которые будем изучать в этой главе. Мы начали эту книгу, заявив, что будем рассматривать целые положительные числа 1, 2, 3…, и в предыдущих главах мы ограничивались только этими числами и дополнительным числом 0. Но теперь мы достигли стадии, на которой целесообразно расширить наши границы, рассматривая все целые числа: 0, ±1, ±2, ±3…. Это никоим образом не повлияет на наши предыдущие понятия; далее, когда мы будем говорить о простых числах, делителях, наибольших общих делителях и тому подобном, мы будем считать их целыми положительными числами. Теперь вернемся к языку сравнений. Если а и b — два целых числа и их разность а — b делится на число m, мы выражаем это записью a ≡ b (mod m) (7.1.1) которая читается так: а сравнимо с b по модулю m. Делитель m мы предполагаем положительным; он называется модулем сравнения. Наше высказывание (7.1.1) означает, что a — b = mk, где k — целое число. (7.1.2) Примеры. 1) 23 ≡ 8 (mod 5), так как 23 — 8 = 15 = 5 3; 2) 47 ≡ 11 (mod 9), так как 47–11 = 36 = 9 4; 3) —11 ≡ 5 (mod 8), так как — 11 — 5 = —16 = 8 (-2); 4) 81 ≡ 0 (mod 27), так как 81 — 0 = 81 = 27 3. Последний пример показывает, что вообще, вместо того, чтобы говорить: число а делится на число m, мы можем записать a ≡ 0 (mod m), так как это означает, что а — 0 = а = mk, где k — некоторое целое число. Например, вместо того, чтобы сказать, что а — четное число, мы можем записать a ≡ 0 (mod 2). Таким же образом видно, что нечетное число является числом, удовлетворяющим сравнению а ≡ 1 (mod 2). Эта несколько странная терминология является довольно обычной для математических работ. § 2. Некоторые свойства сравнений Способ, которым мы записываем сравнения, напоминает нам уравнения, и в действительности, сравнения и алгебраические уравнения имеют много общих свойств. Простейшими из них являются три следующих свойства: a ≡ a (mod m); (7.2.1) это является следствием того, что а — а = m — 0, a ≡ b (mod m) означает, что и b a (mod m). (7.2.2) Это следует из того, что b — a = — (а — b) = m(—k). Из а ≡ b (mod m) и b ≡ c (mod m) (7.2.3) следует, что а ≡ c (mod m), потому что первые два утверждения означают, что а — b = mk, b — с = ml, поэтому а — с = (а — b) + (b — с) = m (k + l). Пример. Из того, что 13 ≡ 35 (mod 11) и 35 ≡ — 9 (mod 11) следует, что 13 ≡ — 9 (mod 11). Мы говорили, что сравнения похожи по своему свойству на равенства. В действительности, мы можем рассматривать равенства как тип сравнения, а именно, сравнения по модулю 0. По определению, а ≡ b (mod 0) означает, что a — b = 0 k = 0 или а = b. Вы почти никогда не встретите такую форму сравнения для записи уравнений в математической литературе. Но существует другое сравнение, очевидно, довольно тривиальное, которое иногда используется. Когда модуль есть число m = 1, мы имеем, что a ≡ b (mod 1) (7.2.4) для любой пары целых чисел а и b, так как это означает, что a — b = 1 k = k (7.2.5) есть целое число. Но предположим теперь на мгновение, что а и b — произвольные вещественные числа, необязательно целые. Тогда тот факт, что они сравнимы по модулю 1, означает, что их разность есть целое число, т. е. эти два числа имеют одинаковую дробную часть. Пример. 8 1/3 ≡ 1 1/3 (mod 1), или 8,333… ≡ 1,333… (mod 1). Вернемся к свойствам обычных сравнений целых чисел; с этого момента мы будем всегда считать, что модуль является целым числом т ≥ 2. Мы можем разделить числовую ось, начиная от начала координат в обоих направлениях на отрезки длиной m, как на рис. 17. Тогда каждое целое число а, положительное или отрицательное, попадает на один из этих отрезков или на одну из точек деления; таким образом, мы можем записать a = km + r, (7.2.6) где k — некоторое целое число, а r— одно из чисел 0, 1, 2…, m — 1. (7.2.7) 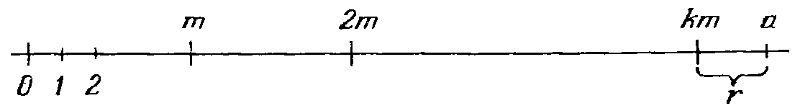 Рис. 17. Это является незначительным обобщением деления положительных чисел, описанного в § 3 главы 4. Здесь мы также называем число r в формуле (7.2.6) остатком при делении числа а на число m или остатком по модулю m. Примеры. 1) а = 11, m = 7, 11 = 7 1 + 4, 2) а = —11, m = 7, —11 = 7 (—2) + 3. Деление (7.2.6) может быть также записано как сравнение а ≡ r (mod m). (7.2.8) Таким образом, каждое число сравнимо со своим остатком по модулю m. В приведенных выше примерах мы имеем 11 ≡ 4 (mod 7), — 11 ≡ 3 (mod 7). Никакие два остатка в (7.2.7) не сравнимы по (mod m), так как разность между любыми двумя из них меньше, чем m. Поэтому два числа, которые не сравнимы по (mod m), должны иметь разные остатки. Итак, мы делаем вывод: сравнение а ≡ b(mod m) выполняется тогда и только тогда, когда числа а и b имеют одинаковые остатки при делении на число m. Существует другой способ представления этого сравнения. Предположим на мгновение, что а и b — целые положительные числа. Мы видели при обсуждении системы чисел в § 2 главы 6, что когда число а записано при основании m, а = (аn…, а1, а0)m, то последняя цифра а0 является остатком числа а при делении его на число m. Если мы используем этот факт, чтобы иначе выразить нашу интерпретацию сравнения, то можно сказать: сравнение а ≡ b (mod m) выполняется для целых (положительных) чисел а и b тогда и только тогда, когда числа а и b имеют одинаковые последние цифры в записи при основании m. Например, 37 ≡ 87 (mod 10), так как эти два числа имеют одну и ту же последнюю цифру в десятичной системе чисел. Система задач 7.2. 1. Найдите остатки —37(mod 7), — 111 (mod 11), — 365 (mod 30). § 3. Алгебра сравнений Из алгебры мы помним, что уравнения можно складывать, вычитать, умножать. Точно такие же правила справедливы для сравнений. Предположим, что мы имеем сравнения a ≡ b (mod m), с ≡ d (mod m). (7.3.1) По определению, это означает, что a = b + mk, c = d + ml, (7.3.2) где k и l — целые числа. Сложим уравнения (7.3.2). В результате получаем а + с = b + d + m (k + l), что можем записать как а + с ≡ b + d (mod m); (7.3.3) другими словами, два сравнения можно складывать. Таким же образом можно показать, что одно сравнение можно вычитать из другого, т. е. что a — c ≡ b — d (mod m). (7.3.4) Пример. 11 ≡ —5 (mod 8) и 7 = — 9 (mod 8). (7.3.5) Складывая их, получаем 18 ≡ — 14 (mod 8), а вычитая, 4 ≡ 4 (mod 8). Оба эти сравнения справедливы. Можно также перемножить два сравнения. Из (7.3.1) и (7.3.2) следует, что ac = bd + m(kd + bl + mkl), таким образом, ас ≡ bd (mod m). (7.3.6) Пример. Когда два сравнения из (7.3.5) перемножены, получается 77 = 45 (mod 8). Сравнение a ≡ b (mod m) может быть умножено на любое целое число с, при этом получаем ас ≡ bc (mod m). (7.3.7) Это можно рассматривать как частный случай умножения сравнений (7.3.6) при с = d. Его можно также рассматривать как прямое следствие из определения сравнения. Пример. Когда первое сравнение из (7.3.5) умножается на 3, получаем, что 33 = -15 (mod 8). Возникает естественный вопрос: в каком случае можно в сравнении (7.3.7) сократить общий множитель с и получить при этом верное сравнение a ≡ b (mod m)? Именно здесь сравнения отличаются от уравнений. Например, верно, что 22 ≡ -2 (mod 8), но сокращение на множитель 2 дало бы сравнение 11 ≡ -1 (mod 8), которое неверно. В одном важном случае сокращение допустимо: если ас ≡ bc (mod m), то a ≡ b (mod m) при условии, что числа m и с взаимно просты. Доказательство. Первое сравнение означает, что ас — bc = (а — b) с = mk. Если D(m, с) = 1, то отсюда следует, что а — b делится на m в соответствии с результатом, доказанным в § 2 главы 4. Пример. В сравнении 4 ≡ 48 (mod 11) мы можем сократить на множитель 4, так как D(11, 4) = 1. Это дает 1 ≡ 12 (mod 11). Система задач 7.3. 1. Придумайте еще несколько примеров на использование изложенных правил действий со сравнениями. § 4. Возведение сравнений в степень Предположим вновь, что имеется сравнение a ≡ b (mod m). Как мы только что видели, можно умножить это сравнение на себя, получив а2 ≡ b2 (mod m). Вообще можно, умножив это сравнение на себя нужное количество раз, получить an ≡ bn (mod m) для любого целого положительного числа m. Пример. Из сравнения 8 ≡ -3 (mod 11) после возведения в квадрат следует сравнение 64 ≡ 9 (mod 11), а после возведения в куб получаем сравнение 512 ≡ -27 (mod 11). Многие результаты теории сравнений связаны с остатками высоких степеней чисел, поэтому покажем, как можно продолжить процесс возведения в степень. Предположим, например, что мы хотим найти остаток сравнения 389 (mod 7). Одним из путей для выполнения этого является повторное возведение в квадрат. Мы находим: 9 = 32 ≡ 2 (mod 7), 34 ≡ 4, 38 ≡ 16 ≡ 2, 364 ≡ 4 (mod 7). Так как 89 = 64 + 16 + 8 + 1 = 26 + 24 + 23 + 1, то отсюда следует, что 389 = 364 • З16 • З8 • 3 = 4 • 4 • 2 • 3 ≡ 5 (mod 7). Таким образом, остаток (по модулю 7) есть 5, или, говоря другими словами, в соответствии с изложенным в § 2, последняя цифра числа З89, записанного в системе счисления при основании 7, равна 5. В действительности, для того чтобы найти этот остаток, мы записали показатель степени 89 = 26 + 24 + 23 + 1 = (1, 0, 1, 1, 0, 0, 1) в двоичной системе счисления. Повторным возведением в квадрат мы нашли остатки (по модулю 7) тех степеней числа 89, которые сами являются степенями числа 2: 1, 2, 4, 8, 16, 32, 64. Соответствующий метод можно использовать для любых других оснований. Однако в частном случае бывает возможность упростить вычисление, если заметить особенности этого случая. Например, в случае, разобранном выше, мы можем отметить, что 33 ≡ -1 (mod 7), З6 ≡ 1 (mod 7), откуда заключаем, что 384 = (36)14 ≡ 1 (mod7). Поэтому 389 = 384 • 33 • 32 ≡ 1 • (-1) • 2 = -2 ≡ 5 (mod 7), как и раньше. В качестве другой иллюстрации сказанного можно рассмотреть числа Ферма, с которыми мы познакомились в § 3 гл. 2: Fn = 22ⁿ+1. Первые пять чисел Ферма таковы: F0 = 3, F1 = 5, F2 = 17, F3 = 257, F4 = 65537. Отсюда можно высказать предположение: десятичная запись всех чисел Ферма, за исключением F0 и F1 оканчивается цифрой 7. Докажем с помощью сравнений, что это действительно так. Очевидно, что оно равносильно утверждению, что числа 22ⁿ, n = 2, 3… оканчиваются цифрой 6. Это можно доказать по индукции. Заметим, что 22² = 16 ≡ 6 (mod 10), 22³ = 256 ≡ 6 (mod 10), 22ˆ4 = 65536 ≡ 6 (mod 10), Более того, если мы возводим в квадрат число 22ˆk, то результатом будет число
Предположим, что для некоторого значения t
возводя в квадрат это сравнение, мы находим, что
что и требовалось. § 5. Теорема Ферма Из алгебры мы знаем правила возведения бинома в степень: (x + у)1 = х + у, (х + у)2 = x2 + 2xy + y2, (x + y)3 = х3 + Зx2y + Зху2 + у3, (x + у)4 = х4 + 4х3у + 6х2у2 + 4ху3 + у4 (7.5.1) и вообще (х + у)p = хр + Cp1xp-1y + Ср2хр-2y2 +… + ур. (7.5.2) Здесь первый и последний коэффициенты равны единице. Средними биномиальными коэффициентами являются Cp1 = p/1, Ср2 = p(p-1)/(1 2), Ср3 = p(p-1)(p-2)/(1 • 2 • 3)… (7.5.3) и вообще Срr = p(p-1)(p-2)… (p — r + 1)/(1 2… r), (7.5.4) Так как эти коэффициенты получаются в результате последовательного умножения на бином (х + у), то ясно, что они являются целыми числами. С этого момента будем считать, что р — простое число. Чтобы записать эти коэффициенты в целочисленном виде, необходимо сократить все общие множители знаменателя 1 • 2 • 3 •… • r и числителя p(p-1)(p-2)… (p — r + 1) Однако знаменатель не содержит простого множителя р, поэтому после сокращения число р останется множителем в числителе. Мы делаем вывод. Все биномиальные коэффициенты (кроме первого и последнего) в выражении (7.5.2) делятся на р, если р — простое число. Пусть теперь х и у в выражении (7.5.2) будут целыми числами. Если мы рассмотрим формулу (7.5.2) как сравнение по модулю р, то можно сделать вывод, что для любых целых чисел х и у и простого р (х + у)p ≡ хр + ур (mod p). (7.5.5) В качестве примера возьмем р = 5: (х + у)5 = х5 + 5х4у + 10x3y2 + 10x2y3 + 5xy4 + у5. Так как все средние коэффициенты делятся на 5, то (х + у)5 ≡ х5 + у5 (mod 5) в соответствии с (7.5.5). Из сравнения (7.5.5) можно сделать важные выводы. Применим его для случая х = у = 1. Получаем 2p = (1 + 1)p ≡ 1p + 1p = 2 (mod p). Возьмем затем х = 2, у = 1 и найдем, что 3p = (2 + 1)p ≡ 2p + 1p; теперь, используя предыдущий результат, 2p ≡ 2 (mod p), получаем 2p + 1p ≡ 2 + 1 ≡ (mod p). Итак, 3p ≡ 3 (mod p). Далее для х = 3, у = 1 получаем 4p ≡ 4 (mod p). Используя этот процесс, можно доказать по индукции, что аp ≡ a (mod p) для всех значений числа а = 0, 1…. р -1. (7.5.6) Случаи a = 0 и а = 1 очевидны. Так как каждое число сравнимо (mod р) с одним из остатков, записанных в (7.5.6), мы делаем вывод: для любого целого числа а и любого простого числа р ap ≡ a (mod p). (7.5.7) Это утверждение обычно называют теоремой Ферма, хотя некоторые авторы называют ее малой теоремой Ферма, чтобы отличить от последней теоремы Ферма, или гипотезы Ферма, о которой мы упоминали в § 3 главы 5. Пример. Для р = 13 и а = 2 мы находим: 13 = 8+ 4 + 1, т. е. 213 = 28+4+1 = 28 24 • 21. Так как 24 = 16 ≡ 3 (mod 13), 28 ≡ 9(mod 13), то 213 = 28 • 24 • 2 ≡ 9 • 3 • 2 ≡ 2 (mod 13), как и утверждает теорема Ферма. В соответствии с правилом сокращения для сравнений, сформулированном в конце § 3, мы можем сократить общий множитель а в обеих частях записи теоремы Ферма (7.5.7) при условии, что число а взаимно просто с числом р, являющимся модулем сравнения. Это дает следующий результат: если а является целым числом, не делящимся на простое число р, то ap-1 ≡ 1 (mod p). (7.5.8) Этот результат также называют теоремой Ферма. Пример. Когда а = 7, р = 19, мы находим, что 72 = 49 ≡ 11 (mod 19) 74 ≡ 121 ≡ 7 (mod 19), 78 ≡ 49 ≡ 11 (mod 19), 716 ≡ 121 ≡ 7 (mod 19), и это дает ap-1 = 718 = 716 • 72 ≡ 7 • 11 ≡ 1 (mod 19), что соответствует утверждению (7.5.8). В качестве приложения теоремы Ферма вновь рассмотрим треугольники Пифагора, обсужденные в гл. 5 и докажем следующее утверждение: произведение длин сторон треугольника Пифагора делится на 60. Доказательство. Очевидно, достаточно доказать это для простейших треугольников. В соответствии с формулой (5.2.7), это произведение есть Р = 2mn (m2 — n2) (m2 + n2) = 2mn (m4 — n4). Число Р делится на 60 тогда и только тогда, когда оно делится на 4, на 3 и на 5. Так как одно из чисел m и n четно, то 2mn, а следовательно, и число Р, делится на 4. Оно делится на 3, если хотя бы одно из чисел m или n делится на 3, но если ни одно из них не делится на 3, то Р все же будет делиться на 3, так как из условий (7.5.8), а также D(m, 3) = 1 и D (n, 3) = 1 следует, что m2 ≡ 1 (mod 3) и n2 ≡ 1 (mod 3), так что m2 — n2 ≡ 1 – 1 = 0 (mod 3). Аналогично, число Р делится на 5. Это очевидно, если m или n делится на 5. Если ни одно из них не делится на 5, то вновь по теореме Ферма (7.5.8) получаем m4 — n4 ≡ 1 – 1 = 0 (mod 5). |
|
||
| Главная | В избранное | Наш E-MAIL | Добавить материал | Нашёл ошибку | Наверх | ||||
|
|
||||

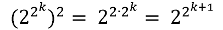
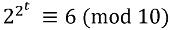 ;
;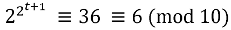 ,
,